Théorème de Pythagore - Définition

Réciproque

La réciproque du théorème de Pythagore est également vraie :

Le théorème de Pythagore est donc une propriété caractéristique des triangles rectangles. Formulé autrement, si dans un triangle ABC on a BC² + AC² = AB², alors ce triangle est rectangle en C.

Variations sur le théorème

Contraposée

La contraposée du théorème affirme ceci :

La contraposée est logiquement équivalente au théorème direct, elle n’a en revanche pas le même usage en démonstration puisque le théorème sert à calculer le troisième côté manquant d’un triangle rectangle, alors que la contraposée sert à démontrer qu’un triangle dont on connaît les longueurs des trois côtés n’est pas rectangle.

Contraposée de la réciproque

Enfin, la contraposée de la réciproque du théorème de Pythagore stipule ceci :

Généralisation à des triangles quelconques

Le théorème d'Al-Kashi est une généralisation du théorème de Pythagore à des triangles quelconques.

Notations usuelles dans un triangle quelconque.

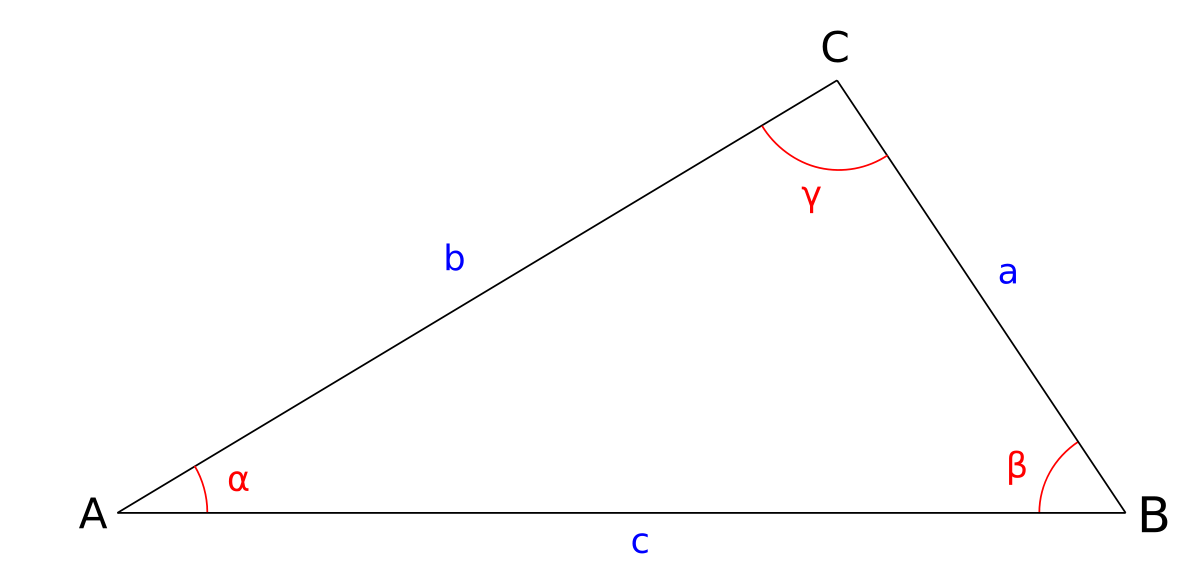
Soit un triangle ABC, dans lequel on utilise les notations usuelles exposées sur la figure c-dessus : d’une part α, β et γ pour les angles et, d’autre part, a, b et c pour les côtés respectivement opposés à ces angles. Alors, le théorème d’al-Kashi s’énonce de la façon suivante : .

Utilisations

• En coordonnées cartésiennes dans un repère orthonormé, le théorème de Pythagore permet d’exprimer la distance entre deux points du plan : ainsi, si A(x_a,y_a) et B(x_b,y_b) sont des points du plan euclidien, la distance les séparant est donnée par : : 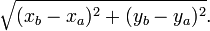: En effet, si C est le point de coordonnées (x_b,y_a), le triangle ACB est rectangle en C, les distances CA et CB sont données par CA= |x_b - x_a| et CB = |y_b - y_a| et la distance AB représente l’hypoténuse du triangle rectangle ACB.
• Plus généralement, dans un espace euclidien (ou dans un espace affine euclidien) de dimension finie, la distance de 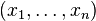à 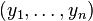s’écrit :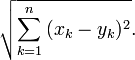
• L’identité de Parseval peut être vue comme une généralisation du théorème de Pythagore aux familles infinies de vecteurs d'un espace préhilbertien.
• Le théorème de Pythagore se généralise aussi dans les simplexes de plus haute dimension. Si un tétraèdre possède un coin formé d’angle droit (un coin de cube), alors le carré de l’aire de la face opposée au coin est la somme des carrés des aires des trois autres faces. Ce théorème est aussi connu sous le nom de théorème de Gua.

Théorème de Pythagore dans d’autres espaces

Écriture vectorielle

En faisant intervenir le concept de vecteur, on peut reformuler le théorème comme suit :

« Étant donnés deux vecteurs et , si et seulement si et sont orthogonaux. »

De manière générale, on a simplement l’inégalité triangulaire : : que l’on écrit en général :

Dans un espace préhilbertien

Le théorème de Pythagore découle en fait directement de la définition du produit scalaire, et se généralise à tout espace préhilbertien. Dans ce cadre général, il affirme que si u et v sont deux vecteurs orthogonaux, alors : :. La réciproque est vraie dans le cas réel. De plus, cette formule se généralise à une famille de vecteurs orthogonaux. Pour elle, la somme des carrées des normes est égale au carré de la norme de la somme. Ce résultat très général permet notamment de démontrer l’inégalité de Bessel, et l’égalité de Parseval.

En géométrie non euclidienne

Cette propriété résiste mal au transfert dans d’autres géométries à cause de leur courbure :

• si la courbure est positive (géométrie sphérique), on obtient : c² < a² + b² ;
• si la courbure est négative (géométrie hyperbolique), on obtient : c² > a² + b² ;
  • en particulier, pour tout triangle rectangle en géométrie hyperbolique, avec une courbure de -1, le théorème de Pythagore prend la forme suivante : 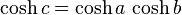où cosh est le cosinus hyperbolique. En utilisant le développement limité d’ordre 2 de cette fonction, on retrouve bien, pour de petites valeurs des côtés, la forme classique du théorème de Pythagore.
• si la courbure est nulle (géométrie plane ou cylindrique), on conserve : c² = a² + b².

Plus précisément, pour tout triangle rectangle sur une sphère de rayon R, le théorème de Pythagore prend la forme suivante :

En utilisant un développement limité d’ordre 2 de la fonction cosinus, on retrouve bien, pour des grandes valeurs de R, la formule classique du théorème de Pythagore.

Espace physique

Comme le théorème de Pythagore est dérivé d’axiomes de la géométrie euclidienne, et que les espaces physiques ne sont pas toujours euclidiens, il ne doit pas être valide pour les triangles dans les espaces physiques. L’un des premiers mathématiciens à réaliser ceci fut Carl Friedrich Gauss, qui mesura donc attentivement de grands triangles rectangles dans le cadre de son étude géographique afin de vérifier ce théorème. Il ne trouva aucun contre-exemple avec sa précision de mesure. La théorie de la relativité générale soutient que la matière et l’énergie conduisent l’espace à être non-euclidien et le théorème ne s’applique donc pas strictement en présence d’énergie. Cependant, la déviation par rapport à l’espace euclidien est faible sauf auprès d’imposantes sources gravitationnelles comme les trous noirs. Déterminer si le théorème est enfreint sur d’importantes échelles cosmologiques, c’est-à-dire mesurer la courbure de l’Univers, est un problème ouvert pour la cosmologie.

Généralisation au tétraèdre

Dans un tétraèdre (OABC) trirectangle en O (tel que (OA),(OB),(OC) sont deux à deux orthogonaux), le carré de l'aire de la face (ABC) opposée à O est la somme des carrés des aires des 3 autres faces.

Ceci se généralise à la dimension n pour un simplexe (O,A₁,...,A_n) où les (OA_i) sont deux à deux orthogonaux : le carré de la mesure de l'hyperface (A₁,...,A_n) est la somme des carrés des mesures des autres hyperfaces.