Suite (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une suite est une famille d'éléments indexée par les entiers naturels. Une suite finie est une famille indexée par les entiers strictement positifs inférieurs ou égaux à un certain entier, ce dernier étant appelé « longueur » de la suite.
Lorsque tous les éléments d'une suite (infinie) appartiennent à un même ensemble E, cette suite peut être assimilée à une application de ![]() dans E. On note classiquement une suite (un), ou
dans E. On note classiquement une suite (un), ou ![]() .
.
Cas particuliers :
- Si
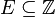 , alors la suite est dite « entière ».
, alors la suite est dite « entière ». - Si
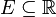 , alors la suite est dite « réelle ».
, alors la suite est dite « réelle ». - Si
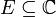 , alors la suite est dite « complexe ».
, alors la suite est dite « complexe ».
Fragments d'histoire
Les suites numériques sont liées à la mathématique de la mesure (mesures d'un phénomène prises à intervalles de temps réguliers) et à l'analyse (une suite numérique est l'équivalent discret d'une fonction numérique). La notion de suite est présente dès qu'apparaissent des procédés illimités de calcul. On en trouve, par exemple, dans la mathématique babylonienne, chez Archimède, spécialiste des procédés illimités d'approximation (séries géométriques de raison 1/4) pour des calculs d'aires et de volumes, ou en Égypte vers 1700 avant Jésus-Christ et plus récemment au 1er siècle après Jésus-Christ dans le procédé d'extraction d'une racine carrée par la méthode de Héron d'Alexandrie :
- Pour extraire la racine carrée de
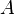 , choisir une expression arbitraire
, choisir une expression arbitraire  et prendre la moyenne entre
et prendre la moyenne entre  et
et 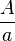 et recommencer aussi loin que l'on veut le processus précédent
et recommencer aussi loin que l'on veut le processus précédent
En notation moderne, cela définit la suite de nombres (un) telle que
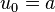 et, pour tout entier
et, pour tout entier 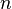 ,
, 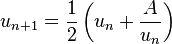
On retrouve ensuite cette préoccupation plusieurs siècles plus tard (à partir du XVIIe siècle) avec la méthode des indivisibles (Cavalieri, Torricelli, Pascal, Roberval). Dans l'Encyclopédie Raisonnée de d'Alembert et Diderot (1751), une grande part est laissée aux suites et séries dont le principal intérêt semble être leur convergence :
- Suite et série : se dit d'un ordre ou d'une progression de quantités qui croissent ou décroissent suivant quelques lois. Lorsque la suite va toujours en s'approchant de plus en plus de quelque quantité finie (...) on l'appelle suite convergente et si on la continue à l'infini, elle devient égale à cette quantité.
C'est ainsi que l'on voit Bernoulli, Newton, Moivre, Stirling et Wallis, s'intéresser aux suites pour approcher des valeurs numériques. C'est à Lagrange que l'on doit, semble-t-il, la notation indicielle. L'étude des suites ouvre la porte à celle des séries entières dont le but est d'approcher, non plus des nombres, mais des fonctions. Dans la seconde moitié du XXe siècle, le développement des calculateurs et des ordinateurs donne un second souffle à l'étude des suites en analyse numérique grâce à la méthode des éléments finis. On en retrouve l'usage aussi dans les mathématiques financières.
Parallèlement à ces études de suites pour leur convergence, se développe un certain goût pour l'étude de la suite non tant pour sa convergence mais pour son terme général. C'est le cas par exemple d'un grand nombre de suites d'entiers comme la suite de Fibonacci, celle de Lucas ou, plus récemment, celle de Syracuse. Sont aussi particulièrement étudiées les suites de coefficients dans des séries entières ou les suites de nombres découvertes lors de dénombrements.