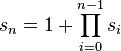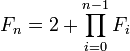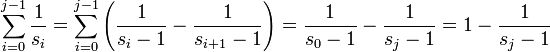Suite de Sylvester - Définition

Introduction

Démonstration graphique de la convergence vers 1 de la somme Chaque rang de n carrés de côté 1/n a une aire totale de 1/n ; l'ensemble des rangs recouvre exactement un carré plus grand, d'aire 1. [Les carrés de côté 1/1807 ou moins sont trop petits pour être dessinés sur le graphique.)

En théorie des nombres, la suite de Sylvester est une suite d'entiers telle chaque terme de la suite est le produit de tous les termes précédents plus 1. Les premiers termes de la suite sont : 2 ; 3 ; 7 ; 43 ; 1 807 ; 3 263 443 ; 10 650 056 950 807 ; 113 423 713 055 421 844 361 000 443 (Voir suite A000058 de l’OEIS). Usuellement, on pose : s₀ = 2.

La suite de Sylvester doit son nom à James Joseph Sylvester qui, le premier, étudia ses propriétés dans les années 1880. Ses termes croissent selon une fonction exponentielle double. La série formée de la somme des inverses de la suite de Sylvester converge vers 1 plus vite que toute autre série somme infinie d'inverses convergeant vers 1.

La relation de récurrence qui définit les termes de la suite permet de factoriser ceux-ci plus facilement que toute autre série de croissance comparable, mais, du fait de la croissance rapide de la série, la décomposition en nombres premiers n'est connue que pour ses premiers termes. Des valeurs extraites de cette suite ont été utilisées pour construire des représentations de 1 sous forme de fraction égyptienne ; des variétés d'Einstein sasakiennes et l'élaboration d'algorithmes résolvant des problèmes difficiles.

Définitions

La suite de Sylvester peut être définie formellement par la relation :

On peut également définir la série par la relation de récurrence [1] :

Les deux définitions étant prises avec s₀ = 2.

Ces deux définition sont équivalentes, comme le montre facilement un raisonnement par récurrence.

Valeurs approchées, valeurs asymptotiques

Les termes de la suite de Sylverster croissent comme une exponentielle double de n. On montre, en particulier, que :

où est l'arrondi inférieur (arrondi par troncation) de la valeur x et où E ≈ 1.264084735305 est la constante de Vardi (suite A076393 de l’OEIS). Cette formule conduit à l'algorithme suivant pour le calcul de s_n :

s₀ est l'entier le plus proche inférieur à E² ; s₁ est l'entier le plus proche inférieur à E⁴ ; s₂ est l'entier le plus proche inférieur à E⁸ ; et pour s_n, prendre E², puis calculer la puissance nième du résultat et l'arrondir à l'entier inférieur le plus proche. Cet algorithme ne serait efficace que s'il existait une autre méthode pour calculer la constante de Vardi que de calculer explicitement les termes de la série de Sylvester et d'en prendre les racines carrées successives...

La croissance en exponentielle double de la suite de Sylvester est comparable à la croissance de la suite des nombres de Fermat F_n. Ceux-ci sont habituellement définis par l'expression en double exponentielle : , mais ils sont aussi définis par un produit très voisin de la définition de la suite de Sylvester :

Lien avec les fractions égyptiennes

La somme des inverses des termes successifs de la suite de Sylvester génère la série infinie [2] :

Cette série infinie converge vers 1. En effet, il résulte de la définition par réccurence [1] que :

La série partielle constituée de la somme des termes de 1/s₀ à 1/s_j se réduit alors à :

Puisque, lorsque j tend vers l'infini, s_j tend également vers l'infini, la série [2] tend vers 1.

Ainsi, la série [2] est une représentation de 1 sous forme de fraction égyptienne infinie :

On peut trouver une représentation de 1 sous forme de fraction égyptienne de longueur quelconque en tronquant la série [2] après un nombre arbitraire de termes et en soutrayant 1 du dénominateur de la dernière fraction :

La somme des k premiers termes de la série [2] constitue la plus proche approximation possible par défaut de 1 à l'aide d'une fraction égyptienne. Par exemple, les quatre premiers termes de la série [2] valent 1805/1806 et par conséquent, pour représenter tout nombre dans l'ouvert (1805/1806 ; 1), une fraction égyptienne doit avoir au moins cinq termes.

On peut interpréter la suite de Sylvester comme le résultat d'un algorithme glouton pour les fractions égyptiennes qui, à chaque étape, choisit le plus petit dénominateur produisant une série partielle de somme inférieure à 1. Réciproquement, on peut considérer les termes après s₀ comme le développement en fraction égyptienne à dénominateurs impairs de 1/2.