Style de Fitch pour la déduction naturelle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le logicien Fitch a proposé une variante de la déduction naturelle où les démonstrations sont présentées de façon linéaire, renonçant à la structure arborescente proposée par Gentzen.
Introduction
Les règles exposées dans ce paragraphe sont celles du calcul des propositions. Elles permettent d’enchaîner logiquement les phrases, c’est-à-dire d'introduire de nouvelles phrases comme conséquences logiques de ce qui a été dit auparavant. À chacun des opérateurs logiques fondamentaux sont associées deux règles de déduction. L'une des règles est une règle d'introduction : elle explique comment prouver une proposition possédant l'opérateur. L'autre règle est une règle d'élimination : elle explique comment utiliser une proposition possédant l'opérateur pour poursuivre le raisonnement.
Introduction et élimination sont nécessaires pour pouvoir démonter et remonter des formules. La recherche d’une déduction logique consiste justement à analyser les prémisses, c’est-à-dire à les démonter, et à réassembler les morceaux pour faire des formules que l’on peut enchainer logiquement jusqu’à la conclusion. On croit parfois qu’il est très difficile de faire des preuves mathématiques, mais dans son principe, ce n’est pas très différent d’un jeu de construction avec des cubes.
Les règles relatives à la conjonction
Pour la conjonction, les règles sont très simples.
La règle d'introduction de la conjonction énonce que, à partir des deux phrases A et B on peut déduire la phrase (A et B).
-
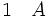
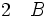
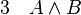 (introduction de la conjonction entre 1 et 2)
(introduction de la conjonction entre 1 et 2)
La règle d'élimination de la conjonction énonce que, à partir de la phrase (A et B), on peut déduire les deux phrases A et B prises séparément.
-
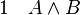
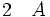 (élimination de la conjonction 1)
(élimination de la conjonction 1)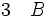 (élimination de la conjonction 1)
(élimination de la conjonction 1)
Ces règles permettent d'assembler ou au contraire de séparer des assertions qui sont toutes considérées comme vraies. C’est la forme logique de la capacité de la raison à analyser le monde, c’est-à-dire à étudier ses parties séparément, et à le synthétiser, c’est-à-dire à rassembler les éléments d’une étude en un tout. C’est pourquoi ces règles sont également appelées les règles de l'analyse et de la synthèse.
Les règles relatives à l'implication
La règle d'introduction de l'implication ou règle de l'abandon d'une hypothèse provisoire énonce que, pour prouver une implication « si P alors Q », il suffit de procéder de la façon suivante : on pose P comme hypothèse provisoire, on fait alors des déductions à partir de toutes les phrases antérieures plus P en vue d’atteindre Q. Une fois Q atteint, on peut alors en déduire « si P alors Q ». Insistons sur un point : Q est démontrée sous l’hypothèse P mais « si P alors Q », elle, ne dépend que des prémisses antérieures. Si on utilise la méthode de Fitch, on peut introduire n’importe quand dans une déduction une hypothèse provisoire. Il suffit de la décaler vers la droite par rapport aux autres prémisses. Tout ce qui est déduit sous une hypothèse provisoire doit être sous elle ou sur sa droite mais jamais sur sa gauche. La règle d'introduction permet de conclure qu'on a prouvé « si P alors Q » sans l'hypothèse P. On peut décaler « si P alors Q » sur la gauche par rapport à P, mais pas par rapport aux autres prémisses utilisées dans la démonstration de Q. On notera :
-
 (hypothèse provisoire)
(hypothèse provisoire) (propriété déduite de 1)
(propriété déduite de 1)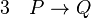 (introduction de l'implication entre les deux lignes 1 et 2)
(introduction de l'implication entre les deux lignes 1 et 2)
La règle d'élimination de l'implication, ou règle du détachement ou du modus ponens énonce que, des deux phrases « P » et « si P alors Q » on peut déduire « Q ». Elle permet de passer de conditions déjà connues, P, à des conditions nouvelles, Q, pourvu qu’il y ait une loi qui l’autorise, « si P alors Q », ce qui sera noté :
-
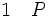
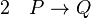
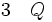 (élimination de l'implication entre les lignes 1 et 2)
(élimination de l'implication entre les lignes 1 et 2)
Montrons par exemple qu’avec ces deux règles on peut déduire « si P alors R » à partir des deux phrases « si P alors Q » et « si Q alors R » :
-
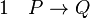 (hypothèse)
(hypothèse)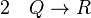 (hypothèse)
(hypothèse) (hypothèse provisoire)
(hypothèse provisoire) (modus ponens sur 3 et 1)
(modus ponens sur 3 et 1) (modus ponens sur 4 et 2)
(modus ponens sur 4 et 2)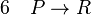 (règle d'introduction de l'implication entre 3 et 5, abandon de l’hypothèse provisoire P).
(règle d'introduction de l'implication entre 3 et 5, abandon de l’hypothèse provisoire P).