Somme directe - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus précisément en algèbre, le terme de somme directe désigne des ensembles munis de certaines structures, construits à partir de la réunion d'autres ensembles du même type.
Somme directe de sous-espaces vectoriels
Somme directe de deux sous-espaces vectoriels
Soient F1 et F2 deux sous-espaces vectoriels de l’espace vectoriel E. On dit que F1 et F2 sont en somme directe si et seulement si pour tout élément u de F1 + F2, il existe un unique couple ![]() de
de ![]() tel que u = u1 + u2.
tel que u = u1 + u2.
On dit aussi dans ce cas que la somme F1 + F2 est directe.
En d'autres termes, la somme de deux sous-espaces vectoriels F1 et F2 est directe si la décomposition de tout élément de F1 + F2 en somme d'un élément de F1 et d'un élément de F2 est unique.
La somme sera alors notée : ![]() .
.
On dispose des caractérisations usuelles suivantes :
- F1 et F2 sont en somme directe si et seulement si, pour tout u1 de F1 et u2 de F2,
- F1 et F2 sont en somme directe si et seulement si
- F1 et F2 sont en somme directe si et seulement s'il existe une base de F1 et une base de F2 qui, mises bout à bout, forment une famille libre.
Cas de la dimension finie : lorsque F1 et F2 sont de dimensions finies, la somme F1 + F2 est directe si et seulement si ![]() .
.
Sous-espaces supplémentaires : deux sous-espaces F1 et F2 de E sont dits supplémentaires lorsque ![]() . Cela signifie que pour tout élément u de E, il existe un unique couple
. Cela signifie que pour tout élément u de E, il existe un unique couple ![]() de
de ![]() tel que
tel que ![]() .
.
Somme directe de plusieurs sous-espaces vectoriels
On peut généraliser la notion de somme directe à une famille finie de sous-espaces vectoriels de E.
On dit qu'une famille ![]() de sous-espaces vectoriels de E est en somme directe si et seulement si, pour tout élément u de la somme
de sous-espaces vectoriels de E est en somme directe si et seulement si, pour tout élément u de la somme 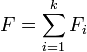 , il existe un k-uplet unique
, il existe un k-uplet unique ![]() de
de ![]() tel que
tel que 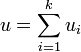 .
.
On dit aussi dans ce cas que la somme F des sous-espaces ![]() est directe.
est directe.
En d'autres termes, la somme est directe si la décomposition de tout élément de 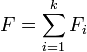 en somme d'éléments des
en somme d'éléments des ![]() est unique.
est unique.
Pour désigner une somme directe, on se sert des notations ![]() ou
ou ![]() .
.
Comme dans le cas de 2 sous-espaces vectoriels, on peut caractériser les sommes directes par l'unicité de la décomposition du vecteur nul :
- La somme
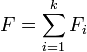 est directe si et seulement si :
est directe si et seulement si : - l'unique k-uplet
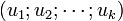 de
de 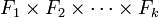 tel que
tel que 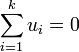 est celui dont tous les éléments sont nuls.
est celui dont tous les éléments sont nuls.
Remarque : dès que la famille comprend au moins 3 sous-espaces, il ne suffit pas pour que la somme soit directe que leurs intersections deux à deux soient réduites à ![]() , c'est-à-dire que :
, c'est-à-dire que :
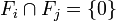 pour tout i et pour tout j, i différent de j.
pour tout i et pour tout j, i différent de j.
On s’en convaincra en regardant dans ![]() les sous-espaces vectoriels :
les sous-espaces vectoriels :
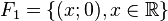
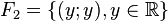
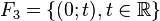 .
.
Leurs intersections deux à deux sont réduites à {(0 ; 0)}, mais leur somme ![]() (égale à
(égale à ![]() ) n'est pas directe.
) n'est pas directe.
En effet, les 3 vecteurs ![]() appartiennent respectivement à
appartiennent respectivement à ![]() ; ils sont non nuls, et tels que
; ils sont non nuls, et tels que ![]() : la décomposition du vecteur nul n'est pas unique.
: la décomposition du vecteur nul n'est pas unique.
En revanche, on montre que les sous-espaces de la famille des ![]() sont en somme directe dans
sont en somme directe dans ![]() si et seulement si :
si et seulement si :
Lorsque les sous-espaces vectoriels sont de dimensions finies, on a encore l'équivalence des assertions suivantes :
- Les
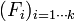 sont en somme directe.
sont en somme directe. 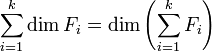 .
.- En concaténant une base
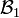 de
de 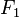 , ... , une base
, ... , une base 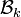 de
de 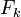 , on constitue une base de la somme.
, on constitue une base de la somme.
Exemple : soient E un espace vectoriel sur K de dimension finie, et f un endomorphisme de E ayant exactement p valeurs propres (distinctes) appelées ![]() . On désigne par
. On désigne par ![]() l'endomorphisme identique de E.
l'endomorphisme identique de E.
Pour tout entier i tel que 1 ≤ i ≤ p, ![]() est le sous-espace propre de f associé à la valeur propre
est le sous-espace propre de f associé à la valeur propre ![]() .
.
Les deux propriétés suivantes sont classiques :
- La somme
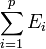 est directe.
est directe. 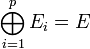 si et seulement si f est diagonalisable.
si et seulement si f est diagonalisable.
- Lorsque c'est le cas, on constitue une base
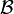 de E diagonalisant f en concaténant une base
de E diagonalisant f en concaténant une base 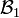 de
de 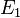 , ... , une base
, ... , une base 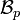 de
de 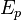 .
.
Somme directe orthogonale
On désigne ici par E un espace préhilbertien réel ou complexe (espace vectoriel réel ou complexe muni d'un produit scalaire). Soit une famille ![]() de sous-espaces vectoriels de E. S'ils sont deux à deux orthogonaux, leur somme est directe. Elle est alors appelée somme directe orthogonale.
de sous-espaces vectoriels de E. S'ils sont deux à deux orthogonaux, leur somme est directe. Elle est alors appelée somme directe orthogonale.
Un exemple très simple est l'espace ![]() constitué des vecteurs orthogonaux à tous les vecteurs d'un sous-espace vectoriel F : il est en somme directe avec F. L'égalité
constitué des vecteurs orthogonaux à tous les vecteurs d'un sous-espace vectoriel F : il est en somme directe avec F. L'égalité ![]() n'est pas toujours vérifiée lorsque la dimension est infinie. Par contre, elle l'est dès que E est de dimension finie.
n'est pas toujours vérifiée lorsque la dimension est infinie. Par contre, elle l'est dès que E est de dimension finie.
Deux espaces qui sont à la fois supplémentaires et orthogonaux sont dits supplémentaires orthogonaux. Un sous-espace vectoriel F de E, même s'il a des supplémentaires, n'en a pas nécessairement un qui lui soit orthogonal. Une condition suffisante est que l'espace F soit complet (ce qui est réalisé en particulier s'il est de dimension finie). Cette question est liée à la possibilité d'effectuer une projection orthogonale.
Lorsque les sous-espaces vectoriels sont de dimensions finies, on a l'équivalence des assertions suivantes :
- Les
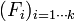 sont en somme directe orthogonale.
sont en somme directe orthogonale. - En concaténant une base orthogonale
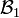 de
de 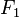 , ... , une base orthogonale
, ... , une base orthogonale 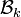 de
de 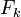 , on constitue une base orthogonale de la somme.
, on constitue une base orthogonale de la somme.