Périmètre - Définition

Fragments d'histoire

Aire et périmètre

Des plans tracés sur des tablettes d'argile et datant d'Ur III (fin du III millénaire av. J.-C.) comportent des mentions de longueurs de terrains, qui sont découpés en triangles et quadrilatères afin de faciliter les calculs. Mais les aires de polygones, notamment les surfaces des champs, étaient calculées à partir des périmètres, même si certains scribes semblent s'être rendu compte que ces raisonnements pouvaient être faux. Cette façon de mesurer des villes ou des régions par leur périmètre est utilisée par Homère pour Troie ou encore par Hérodote :

« aussi donnait-on autrefois le nom d'Égypte à la Thébaïde, dont la circonférence est de six mille cent vingt stades. »

Dès 1800 avant J.-C., les problèmes de géométrie au sujet de périmètres sont attestés. Un problème classique trouvé sur de nombreuses tablettes consistait à trouver les dimensions d'un rectangle, connaissant son aire et son périmètre :

La légende veut que Didon, vers 800 avant J.-C., cherchant une terre pour fonder une nouvelle cité pour son peuple, obtint d'un roi qu'il lui en cède « autant qu'il en pourrait tenir dans la peau d'un bœuf ». Didon découpa une peau de bœuf en très fines lanières et choisit une péninsule : avec les lanières, elle sépara la péninsule du continent et put ainsi délimiter un vaste terrain. Carthage était née. La légende de Didon peut avoir une origine didactique, car elle montre qu'aire et périmètre ne sont pas liés, elle est également une première approche du problème d'isopérimétrie.

La fondation de Rome est également une question de périmètre : Romulus trace, avec sa charrue, le périmètre circulaire de sa future ville. Le mot latin Urbs (la Ville, qui désigne Rome et a donné en français les mots urbain, urbaniser) serait une déformation d'une expression signifiant « tracer le périmètre ». Une racine indo-européenne signifiant pourtour, périmètre, clôture en serait à l'origine.

Le problème de l'isopérimétrie est très ancien, comme l'atteste la légende de Didon, et ses différentes réponses (polygone régulier, demi-disque dans un demi-plan, cercle) était connues dès l'antiquité grecque, bien qu'il ait fallu attendre le XIX^e siècle pour qu'une démonstration rigoureuse soit élaborée.

Circonférence du cercle

Les Babyloniens liaient l'aire A et le périmètre P d'un cercle suivant un algorithme de calcul équivalent à la formule ce qui donne une approximation de π égale à 3. Même lorsqu'ils connaissaient le diamètre d'un cercle, les scribes passaient toujours par le calcul de son périmètre (en multipliant le diamètre par 3) pour ensuite obtenir son aire. La dimension usuelle pour un cercle était toujours son périmètre, jamais son diamètre ni son rayon. Cela montre que, pour les anciens, un cercle était plutôt vu comme une circonférence plutôt que comme une courbe définie par un centre et un rayon. La procédure pour calculer l'aire d'un disque à partir de son diamètre était la suivante, utilisée, dans cet exemple, pour déterminer le volume d'une bûche cylindrique dont le diamètre était 1 + ²⁄₃ :

L'approximation de π par 3 est également utilisée dans la Bible :

« Il fit la mer de fonte. Elle avait dix coudées d’un bord à l’autre, une forme entièrement ronde, cinq coudées de hauteur, et une circonférence que mesurait un cordon de trente coudées. »

et le Talmud :

« Ce qui a trois palmes de tour est large d'une palme. »

Encadrement de cercles par des polygones réguliers. Archimède, pour ses calculs, utilisa des polygones réguliers à 6, 12, 24, 48 et 96 côtés.

Archimède énonça et démontra, dans son traité De la mesure du cercle :

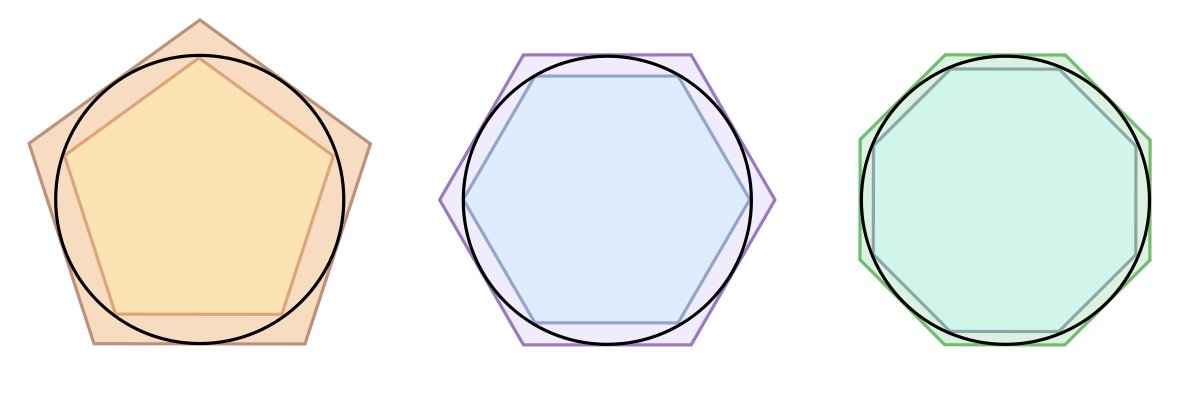
Ce qui donne un encadrement de π (qui est le quotient du périmètre de tout cercle par son diamètre). Pour parvenir à ce résultat, Archimède encadra le cercle par deux polygones réguliers dont il calcula les périmètres. Son résultat utilise des polygones réguliers à 96 côtés.

En 1424, Al-Kashi, dans son Traité sur le cercle, calcule une valeur approchée de π en encadrant le cercle entre deux polygones réguliers à 805 306 368 côtés avec seize décimales exactes. Son objectif était de déterminer une valeur approchée de π suffisamment précise pour pouvoir calculer non seulement la circonférence de la Terre, mais aussi celle de l'Univers. Son traité commence ainsi :

« Louange à Allah, qui connaît le rapport du diamètre à la circonférence [...] et paix à Mahomet, l'Élu, qui est le centre du cercle des prophètes. »

La méthode d'Archimède a été reprise en 1579 par François Viète et en 1593 par Adrien Romain pour calculer de douze à quinze décimales de π.

D'autres mathématiciens ont calculé des valeurs approchées de π en utilisant des calculs d'aires puis, à partir du XVII^e siècle, les techniques du calcul infinitésimal.

Longueur d'une courbe

La question du calcul de la longueur d'une courbe prend, au XVII^e siècle le nom de rectification d'une courbe. Elle est en général considérée comme impossible à résoudre, ce que Descartes exprime par : « ... la proportion qui est entre les droites et les courbes n'étant pas connue, et même je crois ne le pouvant être par les hommes. »

Au XVII^e siècle, l'invention du calcul infinitésimal a conduit à interpréter le calcul de la longueur d'une courbe comme celui d'une intégrale suivant la formule vue plus haut (voir l'exemple de l'ellipse).

Au XIX^e siècle, Camille Jordan donne une nouvelle définition de la longueur d'une courbe, se rapprochant de celle d'Archimède mais utilisant les outils modernes (dont le calcul de la limite d'une suite) : il approche la courbe par un polygone dont les sommets sont des points de cette courbe. Lorsque le nombre de ces points tend vers l'infini, la limite supérieure de la suite des longueurs des polygones obtenus, si elle est majorée, est la longueur de cette courbe. Cette définition de courbe rectifiable englobe et étend la précédente qui utilisait une intégrale.

La côte bretonne.

Durant les XIX^e et XX^e siècles, des mathématiciens découvrent de nombreuses courbes « bizarres » comme celle de von Koch, qui ne sont pas rectifiables. À partir de 1967, Benoît Mandelbrot définit et étudie les fractales à partir d'une question apparemment très simple :

Mandelbrot explique que plus on cherchera à préciser la mesure, plus celle-ci sera grande, jusqu'à éventuellement devenir infinie. En effet, si on mesure grossièrement le périmètre de la Bretagne (ou de tout pays) sur une carte, on va obtenir un polygone. Mais plus la carte sera précise, plus le polygone sera découpé et donc son périmètre grandira. Si l'on veut le « vrai » périmètre de la Bretagne, il faudra aller sur place mesurer chaque caillou, chaque escarpement de rocher, voire chaque atome de ces composants. L'étude de ces objets dépasse le cadre du calcul de périmètres.