Matrice inversible - Définition
La liste des auteurs de cet article est disponible ici.
Autres propriétés et résultats
La matrice inverse d'une matrice inversible A est elle-même inversible, et
- (A−1)−1 = A
Le produit de deux matrices inversibles A et B (de même ordre) est une matrice inversible et son inverse est donné par la relation suivante (on remarquera que l'ordre des matrices est inversé)
- (AB)−1 = B−1A−1
Le produit d'un scalaire non nul k et d'une matrice inversible A est inversible, et son inverse est égal au produit de l'inverse de ce scalaire et de l'inverse de cette matrice.
- (kA)−1 = k−1A−1
Des deux premières de ces propriétés, il résulte que l'ensemble des matrices carrées inversibles d'ordre n constitue un groupe multiplicatif (dont l'élément neutre est la matrice unité d'ordre n); on l'appelle groupe général linéaire et on le note habituellement ![]() , où
, où ![]() est le corps des scalaires.
est le corps des scalaires.
En général, « presque toutes » les matrices carrées d'ordre n sont inversibles. Sur le corps des nombres réels, cela peut être formulé de façon plus précise: l'ensemble des matrices non inversibles, considéré comme sous-ensemble de ![]() , est négligeable pour la mesure de Lebesgue. Intuitivement, cela signifie que si l'on choisit au hasard une matrice carrée d'ordre n à coefficients réels, la probabilité pour qu'elle ne soit pas inversible est nulle. La raison en est que les matrices non inversibles sont les racines (ou zéros) d'une fonction polynomiale donnée par le déterminant.
, est négligeable pour la mesure de Lebesgue. Intuitivement, cela signifie que si l'on choisit au hasard une matrice carrée d'ordre n à coefficients réels, la probabilité pour qu'elle ne soit pas inversible est nulle. La raison en est que les matrices non inversibles sont les racines (ou zéros) d'une fonction polynomiale donnée par le déterminant.
L'ensemble des matrices inversibles est dense dans l'ensemble des matrices carrées réelles ou complexes. En effet on peut approcher toute matrice de Mn(R) (ou Mn(C)) par une suite de matrices inversibles. Par exemple, considérons la suite de matrices de terme général M(k)=M-(1/k).I. Le déterminant de M(k) est une fonction polynomiale en k, il s'annule donc un nombre fini de fois. Ainsi il existe K tel que pour tout k > K , det(M(k)) soit non nul, et donc que M(k) soit inversible. On a donc bien en considérant la suite (M(k)) pour k>K une suite de matrices inversibles qui converge vers M une matrice quelconque, ce qui justifie la densité.
Généralisations
Certaines des propriétés des matrices inverses sont aussi vérifiées par les matrices pseudo-inverses qui peuvent être définies pour n'importe quelle matrice, même pour celles qui ne sont pas carrées.
Au cas où la matrice X n'est pas carrée, il est possible d'inverser grâce à une prémultiplication par le groupe de matrices ![]() ou une postmultiplication par
ou une postmultiplication par ![]()
On a bien:
Dérivée de l'inverse d'une application à valeurs matricielles
- Soient un intervalle I (d'intérieur non vide) de
 et une fonction matricielle
et une fonction matricielle 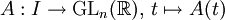 dérivable sur I.
dérivable sur I.
Alors la fonction matricielle ![]() est dérivable sur I et :
est dérivable sur I et :
Cette relation découle de l'identité
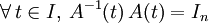 .
.
Pour n=1, en notant f(t) le réel A(t), on retrouve la formule usuelle de dérivation :
- Plus génériquement, l'application
est infiniment différentiable (puisque son expression par la formule des cofacteurs est rationnelle).
Les formules explicites donnant ses différentielles successives se déduisent par récurrence de la première :
-
- En utilisant que inv est différentiable :
L'identité
donne, par différentiation,
d'où
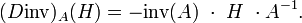
- En feignant d'ignorer que inv est différentiable :
- On démontre d'abord la formule pour A=In : pour K de norme r < 1 (de telle façon que In+K soit inversible),
- En feignant d'ignorer que inv est différentiable :
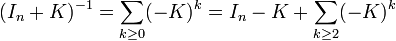
et le reste est majoré par :
donc le quotient de ce reste par r tend vers 0 quand r tend vers 0.
Ceci prouve la formule annoncée, pour A=In :
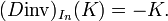
-
- On se ramène ensuite à cette formule, par "translation" :
-
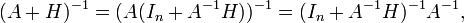
donc