Matrice diagonalisable - Définition
La liste des auteurs de cet article est disponible ici.
Application à l'exponentielle matricielle
Les techniques de diagonalisation dépassent largement le cas de l'algèbre. L'exemple donné ici traite d'un cas d'analyse fonctionnelle. Comme souvent, dans ce contexte, des considérations topologiques supplémentaires sont nécessaires.
Il existe un cas particulier important d'équations différentielles, celui où elles sont linéaires. L'article sur les équations différentielles linéaires nous montre que sa résolution est intimement liée à la résolution de l'équation suivante, où a désigne un endomorphisme :
La fonction exponentielle sur l'espace des endomorphismes est l'unique solution de cette équation. Or, en dimension finie, sur le corps des nombres réels ou complexes, une analyse à l'aide d'une diagonalisation montre que cette fonction s'exprime sous la forme de la série d'endomorphismes suivante :
Cette fonction vérifie de plus la propriété suivante :
Si ab = ba alors exp(a + b) = exp(a)exp(b)
Pour le calcul effectif de la solution, une analyse plus poussée de la réduction des endomorphismes est nécessaire.
La démonstration donnée ici n'est pas la plus générale. Des résultats analogues se démontrent sur les algèbres de Banach.
Il existe une unique fonction exp de la variable réelle ou complexe dans l'espace des endomorphismes de dimension finie sur le corps des réels ou des complexes, vérifiant l'équation suivante :
Cette fonction est définie par :
Démonstration. L'existence et l'unicité sont garanties par le théorème de Cauchy-Lipschitz. La convergence de la série est garantie par son absolue convergence. La démonstration suivante utilise celle de la borne du sup sur la boule unité. Il est à remarquer que la convergence ne suppose pas la dimension finie dans le cas où l'endomorphisme est continu.
Cas où a est diagonalisable. Soit (ei) une base de vecteurs propres, de valeurs propres (λi). Considérons alors l'endomorphisme exp. Il vérifie pour tout élément de la base :
L'équation (1) est donc vérifiée sur une base de l'espace vectoriel pour la fonction exp. Cette équation est linéaire et est donc vérifiée partout.
Cas complexe où a est quelconque. Utilisons alors un argument topologique ; remarquons que l'ensemble des endomorphismes diagonalisables est dense dans l'espace des endomorphismes. Il est donc possible de considérer une suite (ai) d'endomorphismes diagonaux convergeant vers a. Considérons alors la suite de fonctions 
, la suite des dérivées converge uniformément sur toute boule de centre a autour d'une valeur de t donnée. Cette même suite converge simplement. Par passage à la limite, l'égalité (1) est donc vérifiée pour a avec la fonction exponentielle.
Cas réel. Il suffit de prolonger l'espace vectoriel en un espace vectoriel complexe, l'égalité (1) est alors vérifiée. Sa réduction au cas réel est donc aussi vérifiée.
Si ab = ba alors exp(a + b) = exp(a)exp(b).
Démontrons dans un premier temps que les endomorphismes b et exp(a) commutent. Soit ε un réel strictement positif. La série définissant l'exponentielle est absolument convergente, donc il existe un entier p tel que :
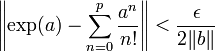
Cette majoration démontre les deux inégalités suivantes :
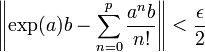
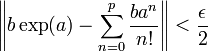
De plus, b commutent avec a donc aussi avec toutes les puissances de a. Ce qui montre, en additionnant les deux majorations précédentes que :
La dernière inégalité démontre la commutativité cherchée.
Recherchons alors une solution à l'équation différentielle suivante :
Les deux calculs suivants :
montrent deux écritures de l'unique solution à l'équation différentielle. L'unicité de la solution prouve alors l'égalité. En particulier si t = 1 on obtient :
La dernière démonstration ne suppose pas la dimension finie, mais la continuité de a et de b.