Matrice diagonalisable - Définition

Propriétés et critères

Par définition, toute matrice semblable à une matrice diagonalisable est également diagonalisable, ce qui peut se traduire pour les endomorphismes par le fait que le conjugué d'un endomorphisme diagonalisable par un automorphisme est également diagonalisable.

Plusieurs autres propriétés se déduisent directement de la forme diagonale :

• le noyau et l'image sont en somme directe ;
• le polynôme caractéristique est scindé : étant un invariant de similitude, il est le même pour une matrice diagonalisable M et pour une matrice diagonale D associée et s'écrit :
  
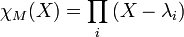
  où (λ_i) décrit les coefficients diagonaux de D (une même valeur pouvant apparaitre plusieurs fois).

En revanche, une matrice dont le polynôme caractéristique est scindé n'est pas forcément diagonalisable, comme dans le cas des matrices nilpotentes non nulles.

Cependant, si le polynôme caractéristique est scindé à racines simples, chacune de ses racines est associée à une valeur propre et les vecteurs propres associés forment une base, montrant que la matrice est diagonalisable.

Puissances et polynômes

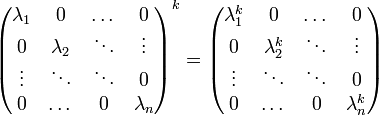
Les puissances d'une matrice diagonalisable s'expriment sous la forme

où la puissance de la diagonale se calcule en élevant simplement chaque coefficient diagonal à la même puissance k.

En conséquence, pour tout polynôme Q, la matrice Q(M) est égale à P.Q(D).P^-1, et Q(D) s'exprime en appliquant simplement Q à chaque coefficient diagonal de D. On en déduit que Q(M) est nulle si et seulement si tous les coefficients diagonaux de D sont des racines du polynôme. Le polynôme minimal de M est donc le produit des facteurs (X-λ), où λ parcourt l'ensemble des coefficients diagonaux de D sans tenir compte de leur éventuelle multiplicité. En particulier, ce polynôme est scindé à racines simples.

Caractérisation

Par les polynômes

La réciproque de la dernière propriété énoncée ci-dessus peut se déduire de la décomposition de Dunford : si une matrice M annule un polynôme scindé, le polynôme minimal de M est scindé lui aussi. La matrice M est alors semblable à la somme d'une matrice diagonale D et d'une matrice nilpotente N dont l'indice de nilpotence est le plus petit commun multiple des ordres de multiplicité de chaque racine du polynôme minimal de M. Si de plus M annule un polynôme scindé à racines simples, alors son polynôme minimal est lui aussi scindé à racines simples, si bien que N est nilpotente d'ordre 1 c'est-à-dire nulle, et M est semblable à la matrice diagonale D.

Par les sous-espaces propres

Pour toute valeur propre λ d'une matrice M, on distingue :

• sa multiplicité géométrique, qui est la dimension du sous-espace propre associé, et
• sa multiplicité algébrique, qui est l'ordre de multiplicité de la racine λ dans le polynôme caractéristique de M (c'est aussi la dimension du sous-espace caractéristique associé).

La matrice M est diagonalisable si et seulement si la somme des multiplicités géométriques est égale à la taille de M. Or chaque multiplicité géométrique est toujours inférieure ou égale à la multiplicité algébrique correspondante. Par conséquent, une matrice est diagonalisable si et seulement si :

• son polynôme caractéristique est scindé et
• pour toute valeur propre, la multiplicité géométrique est égale à la multiplicité algébrique.

Racine

Le fait que toute puissance d'une matrice diagonalisable soit également diagonalisable admet une réciproque partielle. Toute matrice inversible admettant au moins une puissance non nulle diagonalisable est diagonalisable également sur un corps algébriquement clos de caractéristique nulle.

Ce résultat est une conséquence de la caractérisation ci-dessus par les polynômes. Soit A une matrice inversible dont une puissance Aⁿ (avec n > 0) a pour polynôme minimal un polynôme scindé à racines simples s'écrivant :

Puisque A est inversible, sa puissance Aⁿ l'est également donc toutes les racines de P sont non nulles. Il en découle que le polynôme suivant :

est également scindé à racines simples et est annulé par A, qui est donc diagonalisable.

La condition d'inversibilité permet d'exclure les matrices nilpotentes dont une puissance est la matrice nulle qui est diagonalisable. La condition de clôture algébrique peut être affaiblie en supposant simplement que les valeurs propres de A admettent leurs racines d'ordre n dans le corps des coefficients. Enfin, il suffit que la caractéristique du corps soit première avec l'exposant de la puissance diagonalisable pour garantir que ces racines soient simples.