Géométrie algébrique - Définition

Introduction

La géométrie algébrique est un domaine des mathématiques qui, historiquement, s'est d'abord intéressé à des objets géométriques (courbes, surfaces...) dont les coordonnées vérifiaient des équations ne faisant intervenir que des sommes et des produits (par exemple le cercle unité dans le plan rapporté à un repère orthonormé admet pour équation x² + y² = 1). La simplicité de cette définition fait qu'elle embrasse un grand nombre d'objets et qu'elle permet de développer une théorie riche. Les besoins théoriques ont contraint les mathématiciens à introduire des objets plus généraux dont l'étude a eu des applications bien au-delà de la simple géométrie algébrique ; en théorie des nombres par exemple, cela a conduit à une preuve du grand théorème de Fermat.

Cette branche des mathématiques n'a désormais plus grand chose à voir avec la géométrie analytique dont elle est en partie issue.

Histoire

Les premiers travaux de cette nature remontent aux mathématiques arabes. Omar Khayyam proposa une méthode de résolution des équations cubiques par intersection d'un cercle et d'une parabole. Il combina la trigonométrie et les approximations fonctionnelles pour obtenir des méthodes de résolution géométriques des équations algébriques. Cette branche des mathématiques est maintenant appelée algèbre géométrique.

La « Géométrie » de Descartes, inaugurant l'étude des courbes algébriques par les méthodes de la géométrie analytique, marque la deuxième grande étape dans la genèse de cette discipline.

À proprement parler, il faut attendre le début du vingtième siècle pour que la géométrie algébrique naisse comme appartenant à la géométrie à part entière. Cela fut initié par l'école italienne de la fin du XIX^e siècle (Enriques, Chisini, Castelnuovo, Segre...). Ces géomètres étudiaient courbes et surfaces de l'espace projectif (réel et complexe). Ils introduisirent les notions de points voisins et points proches afin d'avoir une interprétation géométrique du théorème de Bezout. Le style assez libre de l'école italienne reste éloigné de la rigueur actuelle. Les travaux du français Emile Picard conduisirent au groupe des diviseurs et au groupe qui porte son nom. On peut aussi mentionner les travaux de Max Noether en Allemagne.

Après 1930, les écoles américaine (Zariski, Mumford...), allemande (Noether, Brauer), russe (Kolmogorov...) et française (Weil, Chevalley...) développèrent sous une forme plus algébrique l'étude des variétés sur un corps commutatif quelconque en utilisant essentiellement la théorie des anneaux.

Dans les années 50, elle fut totalement transformée par les travaux de l'école française sous l'impulsion de Samuel, d'Henri Cartan, de Serre et d'Alexandre Grothendieck.

En une décennie, le domaine se développa, répondant à des questions classiques sur la géométrie des variétés algébriques. Des applications furent très vite trouvées en théorie des nombres. Jean-Pierre Serre et Alexander Grothendieck établirent les bases de la théorie des faisceaux, et la notion de schéma s'imposa vers 1960.

La démonstration du théorème de Fermat-Wiles est un exemple notable d'application à la théorie des nombres de concepts de géométrie algébrique : les courbes elliptiques, et en cela est un des grands succès de la théorie.

Le théorème de Bézout

On peut assez vite remarquer que si deux courbes planes n'ont pas de composante commune, alors elles se coupent en un nombre fini de points. Ce nombre est majoré par le produit des degrés des deux courbes (une application du résultant peut le justifier). Ainsi une conique rencontre au plus deux fois une droite. Le théorème de Bézout affirme qu'il s'agit en fait d'une égalité à condition de se plonger dans le bon cadre.

Le premier obstacle est l'absence de points de rencontre : typiquement le cercle Z(x² + y² − 1) et la droite Z(y − 2) ne se coupent pas. C'est un problème algébrique ; pour palier ce défaut il faut autoriser les coordonnées à vivre dans une clôture algébrique du corps de base.

On rencontre le second obstacle en observant deux droites parallèles, qui justement ne se coupent pas. C'est un problème qu'on pourrait qualifier de « global ». On y remédie en considérant qu'elles se rencontrent à l'infini. Plus précisément on identifie un point à la droite passant par l'origine et le point . Les autres droites, celles contenues dans z=0, sont les points qui nous manquaient, et toutes ensembles elles constituent l'espace projectif associé à k². Par exemple partant de Z(y) et Z(y-1), on associe les variétés « homogénéisées » Z(y) et Z(y-z) de , i.e. les droites passant par l'origine et les points (z=1,y=0) et (z=1,y=1) respectivement, mais aussi, et on trouve notre point d'intersection, la droite Z(y,z).

Le dernier obstacle vient des points de contact multiple : la parabole Z(y − x²) et la droite Z(y) se coupent uniquement en (0,0) même dans ) : il faut considérer les équations zy-x²=0 et y=0 qui ont pour seule droite commune (y=0, x=0). Pour y remédier, il faut définir la notion de multiplicité, c'est un problème qu'on pourrait qualifier de « local ». Dans l'exemple précédent l'objet à considérer est k[X,Y] / (Y − X²,Y)˜k[X] / (X²), k-algèbre de dimension vectorielle 2 qui reflète la « multiplicité ».

On est alors amené à considérer des objets plus généraux. A l'instar de ce qui se fait en géométrie différentielle, il s'agira d'objet globaux qui localement ressemblent à nos modèles : les variétés affines. On commencera donc par caractériser les variétés affines de façon intrinsèque, i.e. qui ne fera pas référence au choix d'un système de coordonnées. Avant cela voyons une « application » d'un problème d'intersection. L'équation x²+y²=1 représente le cercle centré en l'origine et de rayon 1. Il passe par le point (-1,0), par suite toute droite passant par ce point « doit » recouper le cercle (a priori peut-être sur des points complexes à l'infini...). Une telle droite est « caractérisée » par sa pente t, à condition de s'autoriser pour la droite verticale x=-1 (en résumé : la famille des droites passant par un point donné est paramétrée par la droite projective). Une telle droite D_t, d'équation y=t(x+1), recoupe le cercle en un point vérifiant alors où l'on a développé puis factorisé par la racine évidente (car D_t passe par (-1,0)) x=-1. L'autre point d'intersection est donc 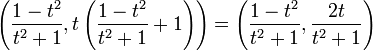, pour et (-1,0) pour (remarquer que dans le cas de cela est cohérent avec les limites). Par rapport au paramétrage réel en (cosθ,sinθ) celui-ci à le mérite de ne faire intervenir qu'une fonction rationnelle (des sommes, produits, divisions), alors que cosinus et sinus n'en sont pas.

Une telle paramétrisation peut permettre de résoudre quelques problèmes. Cela conduit en effet à une description des triplets pythagoriciens et cela permet également d'intégrer toute fonction rationnelle en cosθ,sinθ (au vu du dessin et du théorème de l'angle au centre il s'agit du changement de variable ). L'existence d'une telle paramétrisation est un fait remarquable ; de telles courbes sont dites unicursales. C'est par exemple le cas de :

• Z(y² − x³) paramétrée par (t³,t²) obtenu par les droites D_t = Z(y − tx) passant par le point double (0,0),
• Z(y² − (x + 1)x²) paramétrée par (t² − 1,t³ − t) obtenu par les droites D_t = Z(y − tx) passant par le point double (0,0).

Mais ce n'est pas le cas de xⁿ + yⁿ = 1 pour n>2, sinon avec des paramètres rationnels on obtiendrait une infinité de solution à coefficients rationnels (car il existe déjà (1,0)) ce qui contredirait le grand théorème de Fermat. [ et un petit truc sur les intégrales elliptiques...]