Forme bilinéaire - Définition

Espace vectoriel normé

Pour aller plus loin dans l'étude des formes bilinéaires dans le cas de la dimension infinie, une hypothèse supplémentaire est utile. Elle consiste à associer à l'espace vectoriel une topologie. Un cas particulier fréquent est celui où cette topologie dérive d'une norme conférant à l'espace une structure métrique. Cas particulier de formes bilinéaires est particulièrement étudié, celui où elles sont continues. Dans ce contexte, les isomorphismes généraux sont des isométries et la complétude naturelle du dual topologique apporte des propriétés fortes à l'espace des formes bilinéaires. Les relations d'orthogonalités se précisent si une hypothèse supplémentaire est faite sur les sous-espaces vectoriel : la fermeture.

Dans ce paragraphe, E et F désigne deux espaces vectoriels normés sur un corps K égal à R ou C et donc complet. La forme bilinéaire dont on parle par défaut est toujours notée (.|.).

Forme bilinéaire continue

La continuité des formes bilinéaires suit des règles proches de celles des opérateurs, terme généralement utilisé pour désigner les applications linéaires lorsque la dimension n'est pas finie.

• Les quatre propositions sont équivalentes :

• La forme bilinéaire est continue en tout point de ExF.
• La forme bilinéaire est continue en (0,0)
• L'image du produit cartésien des deux boules unités est bornée.
• 

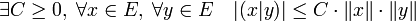
Les isomorphismes ψ₁ et ψ₂ offre une nouvelle condition nécessaire et suffisante pour la continuité de la forme bilinéaire :

• La forme bilinéaire b est continue si et seulement si ψ_1b l'est. Alors ψ_2b l'est aussi.

Si ψ_2b est continue, il est alors évident que la forme bilinéaire et ψ_1b le sont aussi.

• En dimension finie, toute forme bilinéaire est continue.

La situation est analogue à celle des opérateurs. En dimension finie, ils sont tous continus et dans le cas général, il existe une quadruple équivalence entre des propositions de la même nature que celles présentées ici.

• L'ensemble des formes bilinéaires continues est un sous-espace vectoriel de l'espace des formes bilinéaires.

• Si une forme bilinéaire est continue en (0,0) alors la proposition suivante est vraie :

Si la forme linéaire est continue alors elle l'est au point formé par les deux vecteurs nuls. Comme l'image de ce point par la forme bilinéaire est nulle, on obtient :

Ce qui peut encore s'écrire :

Cette dernière majoration prend la forme (1), si C est égal à ε/μ².

• La proposition (1) est vraie si et seulement si l'image du produit cartésien des deux boules unités est bornée :

Si la proposition (1) est vraie, alors il suffit de constater que l'image du produit cartésien des deux boules unités est bornée par C.

Réciproquement si l'image du produit cartésien des deux boules unités est bornée par une constante C et si x (resp. y) désigne un vecteur non nul de E (resp. F), alors :

Et la proposition (1) est vraie.

• Si la proposition (1) est vraie, alors la forme bilinéaire est continue sur ExF :

Soit ε un réel strictement positif, (x₀, y₀) (resp. (h, k)) un point de ExF. La proposition (1) et la bilinéarité de la forme établissent que :

Soit μ le réel strictement positif égal au minimum de 1 et de ε/3C. Alors :

Ce qui démontre la continuité de la forme bilinéaire sur ExF.

Pour conclure il suffit de remarquer que la continuité de la forme bilinéaire sur ExF implique celle au point (0,0).

• La forme bilinéaire best continue si et seulement si ψ_1b l'est. Alors ψ_2b l'est aussi :

La proposition précédente montre que la forme bilinéaire est continue revient à dire que :

Dire que ψ₁ est continue signifie que l'image de la boule unité de E est bornée dans F^*. Autrement dit :

L'égalité entre la forme bilinéaire b et <ψ_1b(.),.> permet de conclure.

• L'ensemble des formes bilinéaires continues est un sous-espace vectoriel de l'espace des formes bilinéaires :

Cette espace est en effet l'intersection du sous-espace vectoriel des formes continues et du sous-espace vectoriel des formes biliénaires sur ExF. L'espace vectoriel sous-jacent est celui des applications de ExF dans K.

 

Espace des formes bilinéaires continues

Le fait de munir E et F d'une norme et de limiter l'étude aux formes bilinéaires continues possède de multiple conséquences sur l'espace des formes bilinéaires. Dans ce paragraphe ne sont considérés que les applications linéaires, formes linéaires et formes bilinéaires continues.

• L'espace des formes bilinéaires sur ExF est normé par la norme des opérateurs.

Si suffit pour cela de définir la norme d'une forme bilinéaire de la borne supérieur de l'image de la valeur absolue ou du module de la forme bilinéaire sur le produit cartésien des deux boules unités.

Ici B_E(1) (resp. B_F(1)) désigne la boule unité de rayon un de E (resp. de F). Pour s'en convaincre, il suffit de remarquer que cette norme est l'image de la norme des opérateurs de L(E, F^*) par l'isomorphisme ψ₁, en conséquence :

• L' application ψ₁ (resp. ψ₂) est une isométrie de L₂(E,F;K) dans L(E,F^*) (resp. L(F,E^*)) si les espaces sont munis de la norme des opérateurs.

Si un espace est complet l'ensemble des applications linéaires continues dans cet espace est aussi complet (cette propriété est démontrée dans l'article Espace vectoriel normé). Comme K est complet L(F,K), c'est-à-dire F^* l'est aussi. L'espace vectoriel des opérateurs de E vers F^* munis de la normes des opérateurs est aussi complet, en conséquence :

• L'espace des formes bilinéaires sur ExF est complet.

Si F est complet et muni d'un produit scalaire (.|.), alors F est qualifié d'espace de Hilbert. Dans ce cas, le théorème de représentation de Riesz indique qu'il existe un isomorphisme isométrique entre F et son dual. C'est l'application qui à un vecteur x associe la forme (x|.), en conséquence :

• L'application qui à tout opérateur a de E vers F associe la forme bilinéaire noté (.|.)_a suivante est un isomorphisme isométrique.

La configuration est la même qu'en dimension finie.

Orthogonalité

L'orthogonalité prend une forme un peu différente pour les espaces topologiques. Ici la forme bilinéaire est toujours continue. Soit Φ une famille de E, alors :

• L'orthogonal de Φ est un sous-espace vectoriel fermé de F.

En effet, soit (u_n) une suite de limite u d'élément de l'orthogonal de F et x un élément quelconque de Φ, la continuité de la forme bilinéaire montre que :

La dernière implication montre le caractère fermé de l'orthogonal de Φ. Sa structure d'espace vectoriel est déjà démontrée.

Un argument analogue à celui du paragraphe sur les orthogonaux montre que l'orthogonal de contient l'adhérence de la somme de l'espace vectoriel engendré par Φ et du noyau à gauche de la forme bilinéaire. Cependant, l'égalité n'est pas toujours vraie. Les égalités entre la somme et l'intersection d'othogonaux reste valable car la démonstration n'utilise aucune hypothèse sur la dimension.