Forme bilinéaire - Définition

Exemples

L'espace euclidien usuel

L'espace R³ formé des triplets de nombres réels (x, y, z) peut être muni d'une forme bilinéaire nommée produit scalaire canonique. S'il est noté (.|.), il est défini par :

L'espace R³ muni de son produit scalaire est qualifié d'euclidien.

La forme bilinéaire duale

Un tel espace est équipé d'une autre forme bilinéaire importante définie à l'aide de l'espace dual R^3* . Il correspond à l'ensemble des formes linéaires, c'est-à-dire les applications linéaires de R^3* dans son corps de nombres R. Cette forme bilinéaire est l'application de R^3*xR³, qui au couple (d ^*, x) associe <d ^*, x> désignant l'image de x par la forme linéaire d ^*. À certains égards, elle ressemble à l'exemple précédent.

Soit (e₁, e₂, e₃) la base canonique de R³, notons d_i l'image <d ^*, e_i> de e_i par d ^* et d le vecteur de R³ (d₁, d₂, d₃). La propriété suivante est vérifiée :

Il existe donc une certaine équivalence entre les deux formes bilinéaires et toute forme linéaire est représentée par un vecteur de R³ à l'aide du produit scalaire.

Remarque : La notation <d ^*, x>_R³ désigne l'image de x par d ^* dans l'espace R³. Elle est appelée crochet de dualité. Quand il n'existe pas de risque d'ambiguité, le nom de l'espace vectoriel est omis. Cette notation est souvent utilisée pour la forme linéaire canonique entre un dual et son espace. On la trouve aussi dans la littérature pour désigner d'autres formes bilinéaires, comme des produits scalaires.

Un espace fonctionnel

Considérons maintenant l'espace E des fonctions continues du segment [0, 1] dans R. Une forme bilinéaire joue un rôle clé sur E. Elle est définie de la manière suivante :

Encore une fois l'espace E possède l'autre forme bilinéaire, celle définie sur E^*xE qui à tout couple d'un élément d ^* du dual de E et d'un élément f de E associe <d ^*, f> l'image par d ^* de f. Néanmoins la géométrie de E diverge de celle de l'exemple précédent. Soit δ la forme linéaire qui, à toute fonction f de E associe f(0). Elle correspond bien à un élément de E^*, mais ne peut pas se représenter par une fonction de E. Une telle forme linéaire porte le nom de fonction δ de Dirac. En un sens, le dual de E est trop vaste pour pouvoir être représenté par les fonctions de E.

Il n'est pas étonnant que des différences de cette nature retentissent sur l'étude des formes bilinéaires.

Définitions

Les formes bilinéaires s'appliquent dans un contexte vaste, en conséquence de multiples définitions sont associées à ce concepts. Ce paragraphe en décrit certaines, qui s'appliquent dans de nombreuses situations. Il en existe d'autres, développés dans les articles dédiés.

Définitions générales

Une forme désigne en mathématiques une application d'un espace vectoriel dans son corps de nombre (le corps de nombre désigne l'ensemble des nombres définissant la multiplication externe des vecteurs, en général ce sont les nombres réels ou complexes). Une forme bilinéaire est une application définie sur un couple de vecteurs x et y, son espace de départ est le produit cartésien de deux espaces vectoriels E et F ayant le même corps de nombres. Lorsque E et F désignent le même ensemble, on parle de forme bilinéaire sur E. (x|y) est une notation fréquente pour désigner l'image du couple (x,y) par la forme bilinéaire ; elle est utilisée dans le reste de l'article.

La forme est dite linéaire pour sa première variable si pour tout y₀, l'application qui à x associe (x|y₀) est linéaire. De même la forme est dite linéaire pour sa deuxième variable si pour tout x₀, l'application qui à y associe (x₀|y) est linéaire. Si les deux propriétés précédentes sont vérifiées, alors la forme est dite bilinéaire.

• Soit (.|.) une application de ExF dans K. La fonction (.|.) est dite bilinéaire si et seulement si elle est linéaire en ses deux variables.

Remarque : À toute forme bilinéaire sur un espace E est associée une forme quadratique. C'est l'application qui à un vecteur x associe le scalaire (x|x). Plus précisément, l'application qui, à chaque forme bilinéaire symétrique associe sa forme quadratique est un isomorphisme. L'isomorphisme réciproque associe à la forme quadratique χ la forme bilinéaire (.|.) définie par :

• La forme bilinéaire (.|.) définie par la ligne ci-dessus est dite forme polaire de la forme quadratique χ.

Remarque : Dans le cas des nombres complexes, il existe une autre forme disposant d'une linéarité différente et souvent plus intéressante, on parle alors de forme sesquilinéaire.

Par défaut, dans le reste de l'article E et F sont deux espaces vectoriels sur un même corps K et (.|.) désigne une forme bilinéaire. Une forme bilinéaire peut aussi être désignée par une lettre, par exemple b, alors (.|.)_b désigne aussi cette forme bilinéaire.

Définitions associées à l'orthogonalité

La notion d'orthogonalité entre deux vecteurs, pour une forme bilinéaire, généralise celle de perpendicularité dans le cas d'un espace euclidien.

• Deux vecteurs x de E et y de F sont dits orthogonaux si l'image du couple (x, y) par la forme bilinéaire est nulle.

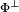• L'ensemble des vecteurs orthogonaux à tous les éléments d'une famille Φ de vecteurs est un sous-espace vectoriel, appelé orthogonal de Φ et souvent noté .

Si E est égal à F et que la forme bilinéaire n'est pas symétrique, pour éviter les confusions, on parle d'orthogonal à droite et à gauche. Un cas particulier, l'orthogonal du vecteur nul, donne lieu à une définition spécifique.

• Le noyau à gauche d'une forme bilinéaire sur un espace ExF est le sous-espace 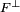, constitué des éléments x de E tels que :

On définit de même un noyau à droite .

Dans le cas où F=E, pour que les noyaux à gauche et à droites soient égaux, il n'est pas nécessaire que la forme soit symétrique ; il suffit qu'elle soit réflexive :

• Une forme bilinéaire est dite réflexive si la propriété suivante est vérifiée:

.

Définitions associées au cas où E est égal à F

Dans le cas ou E est égal à F, il existe des propriétés spécifiques pour les formes bilinéaires. Dans ce paragraphe, la forme linéaire est définie sur ExE.

• Une forme bilinéaire est dite symétrique si et seulement si la propriété suivante est vérifiée :

• Une forme bilinéaire est dite antisymétrique si et seulement si la propriété suivante est vérifiée :

• Une forme bilinéaire est dite alternée si et seulement si la propriété suivante est vérifiée :

• Une forme bilinéaire est dite définie si et seulement si la propriété suivante est vérifiée :

Toute forme alternée est antisymétrique. Si le corps n'est pas de caractéristique deux, alors les deux notions sont équivalentes. Dans le reste de l'article, le corps K est supposé de caractéristique différente de deux.

• Une forme bilinéaire symétrique est dite non dégénérée si et seulement si la propriété suivante est vérifiée :

Une forme bilinéaire symétrique définie est donc non dégénérée.

Pour la propriété suivante, le corps K est supposé totalement ordonné, comme par exemple celui des réels.

• Une forme bilinéaire est dite positive si et seulement si la propriété suivante est vérifiée:

Grâce à l'inégalité de Cauchy-Schwarz, une forme (bilinéaire symétrique) positive non dégénérée est définie.