Espace vectoriel - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En algèbre linéaire, un espace vectoriel est un ensemble muni d'une structure permettant d'effectuer des combinaisons linéaires.
Étant donné un corps (commutatif) K, un espace vectoriel E sur K est un groupe commutatif (dont la loi est notée +) munie d'une action compatible de K (voir la définition exacte). Les éléments de E sont appelés des vecteurs, et les éléments de K des scalaires.
Pour une introduction au concept de vecteur, voir l'article Vecteur.
Définitions
Espace vectoriel
![](https://static.techno-science.net/illustration/Definitions/1200px/g/giuseppe-peano_90281579f2dfb1f28337f328df37b883.jpg")
Soit K un corps commutatif. La définition des espaces vectoriels repose sur la structure de corps mais le lecteur peut lire K comme le corps des réels ou celui des complexes. Un espace vectoriel sur K, ou K-espace vectoriel, est un ensemble E, dont les éléments sont appelés vecteurs, muni de deux lois :
- Une loi interne « + »
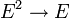, appelée addition ou somme vectorielle, - Une loi de composition externe à gauche « • »
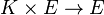, appelée multiplication par un scalaire,
ces deux lois étant assujetties aux relations suivantes.
- 1. La loi « + » est associative. Elle admet un élément neutre, pouvant être noté 0 ou 0E, appelé vecteur nul. Tout vecteur v a un opposé, noté -v. Autrement dit, (E,+) est un groupe, pour tous vecteurs u, v et w de E :
| u+(v+w) | = | (u+v)+w | |||
| 0E +v | = | v | u+(-u) | = | 0E |
- 2. La loi « • » est distributive à gauche par rapport à la loi « + » de E, distributive à droite par rapport à l'addition du corps K, et associative à droite par rapport à la multiplication dans K. Enfin, l'élément neutre multiplicatif du corps K, noté 1, est neutre à gauche pour la loi externe « • », c'est-à-dire que l'on a les identités suivantes pour tous vecteurs u, v de E, et pour tous scalaires λ, μ :
| λ •( u + v ) | = | ( λ • u ) + ( λ •v ) | ( λ + µ ) • u | = | ( λ • u ) + ( µ • u ) |
| (λμ) • u | = | λ • ( µ • u) | 1 • u | = | u |
De l'axiome 1, il découle que E est nécessairement non vide. L'axiome 2 implique que l'élément neutre additif « 0K » du corps K, qui est absorbant sur K, est donc « absorbant » à gauche pour la loi • (le produit par un vecteur quelconque vaut 0E). On en déduit aussi que 0E est absorbant à droite pour la loi •. On peut également démontrer aisément que la loi + est commutative, ce qui fait de (E,+) un groupe abélien. Enfin, -v, l'opposé de v est le produit de v par le scalaire -1, ce qui résulte encore de l'axiome 2. On a donc pour tout vecteurs u de E, et tout scalaire λ :
| 0K • u | = | 0E | λ • 0E | = | 0E | -1 • u | = | -u |
Si 
, 
ou 
, on parle respectivement d'espace vectoriel rationnel, réel ou complexe. Les vecteurs (éléments de E) ont été ici écrits avec des lettres latines italiques, mais certains auteurs les notent par des lettres en gras, ou les surmontent d'une flèche.
Combinaison linéaire
Les deux opérations sur un espace vectoriel permettent de définir la combinaison linéaire, c'est-à-dire la somme finie de vecteurs affectés de coefficients (scalaires). La combinaison linéaire d'une famille de vecteurs 
ayant pour coefficients 
est le vecteur de E donné par :
.
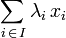Lorsque l'ensemble d'indexation 
est infini, il est nécessaire de supposer que le support de la famille soit fini. Rappelons que le support est l'ensemble des indices i pour lesquels λi est non nul. L'intérêt de la structure d'espace vectoriel réside en la possibilité d'effectuer des combinaisons linéaires.
Sous-espace vectoriel
![](https://static.techno-science.net/illustration/Definitions/1200px/l/linear-subspaces-with-shading.svg_14bf7b87bed73f8c7f8408bf1a7f0993.png")
Un sous-espace vectoriel de E est une partie non vide F de E stable par addition vectorielle et multiplication par un scalaire, ou de manière équivalente, stable par combinaisons linéaires. Une partie F est un sous-espace vectoriel ssi elle vérifie les deux propriétés suivantes :
- F est un sous-groupe additif de (E,0,+), ie F contient 0, la somme de deux éléments de F est un élément de F, et l'inverse d'un élément de F pour la loi additive est un élément de F ;
- Le produit d'un scalaire par un vecteur de F appartient à F.
Muni des lois induites, F est alors un espace vectoriel. L'intersection d'une famille quelconque (finie ou infinie) de sous-espaces vectoriels est un sous-espace vectoriel mais l'union, même finie, n'en est pas un en général. La somme de deux sous-espaces vectoriels F et G est la partie
,
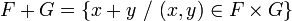qui est toujours un sous-espace vectoriel de E. C'est le plus petit sous-espace vectoriel (au sens de l'inclusion) de E contenant F et G. Cette construction se généralise à une famille quelconque de sous-espaces vectoriels.
Deux sous-espaces vectoriels F et G de E sont dits en somme directe lorsque leur intersection est l'espace nul. Leur somme est alors notée 
. Les sous-espaces vectoriels F et G sont dits supplémentaires (l'un de l'autre) dans E s'ils sont en somme directe et que 
. L'axiome du choix permet d'assurer l'existence d'un supplémentaire à tout sous-espace vectoriel, mais il n'y a jamais unicité (sauf dans le cas du sous-espace nul ou de l'espace total). Si E est la somme directe de F et G, tout vecteur de E se décompose alors de manière unique en une somme de deux vecteurs, l'un appartenant à F et l'autre à G. Plus généralement, une famille de sous-espaces vectoriels (Fi) est dite en somme directe dans E si tout vecteur de E s'écrit de manière unique comme une somme 
avec pour tout i, 
. Cette définition implique que les sous-espaces vectoriels Fi soient d'intersection nulle deux à deux et que leur somme soit égale à E mais la réciproque est fausse.