Espace vectoriel - Définition

Structures connexes

Structures relatives

• Une paire d'espaces vectoriels est la donnée d'un espace vectoriel et d'un sous-espace vectoriel de celui-ci.
• Plus généralement, un espace vectoriel peut être filtré par la donnée d'une famille de sous-espaces vectoriels croissante ou décroissante.
• Un drapeau sur un espace vectoriel de dimension n est la donnée de n sous-espaces vectoriels emboîtés, de dimensions croissantes de 1 en 1.
• Un espace vectoriel de dimension fini peut être orienté par le choix d'une orientation sur ses bases.
• Un espace vectoriel gradué est une famille d'espaces vectoriels, généralement indexée par , ou 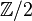. Un morphisme entre deux tels espaces vectoriels gradués est alors une famille d'applications linéaires qui respecte la graduation.

Structures algébriques

• Un module M sur un anneau A est un groupe additif muni d'une loi externe sur M à coefficients dans A, compatible avec l'addition sur M et avec les opérations sur A. Mais il ne dispose en général ni de base ni de supplémentaires.
• Une algèbre est un espace vectoriel muni d'une multiplication distributive par rapport à l'addition et compatible avec la loi de composition externe.
• Une algèbre de Lie est un espace vectoriel muni d'un crochet de Lie compatible avec la loi de composition externe.

Structures topologiques et géométriques

• Un espace affine est un ensemble muni d'une action libre et transitive d'un espace vectoriel.
• Un espace vectoriel euclidien est un espace vectoriel réel de dimension finie muni d'un produit scalaire.
• Un espace vectoriel réel ou complexe est dit normé lorsqu'il est muni d'une norme. Par exemple, les espaces de Banach, dont les espaces de Hilbert qui généralisent la notion d'espace vectoriel euclidien, sont des espaces vectoriels normés.
• Si K est un corps muni d'une topologie, un espace vectoriel topologique sur K est un K-espace vectoriel muni d'une topologie compatible, c'est-à-dire que l'addition et la multiplication par un scalaire doivent être continues. C'est le cas entre autres des espaces vectoriels normés et des espaces de Fréchet.
• Un fibré vectoriel est une surjection d'un espace topologique sur un autre, telle que la préimage de chaque point soit munie d'une structure d'espace vectoriel compatible continûment avec les structures des préimages des points voisins.

Famille de vecteurs et dimension

Indépendance linéaire

Une famille de vecteurs de E est dite libre (sur ) ou encore les vecteurs de cette famille sont dits linéairement indépendants, si toute combinaison linéaire d'éléments de cette famille à coefficients non tous nuls est non nulle. Cette condition équivaut à ce que la seule combinaison linéaire nulle d'éléments de est celle dont tous les coefficients sont nuls. Dans le cas contraire, la famille est dite liée et les vecteurs la constituant sont dits linéairement dépendants. Comme une combinaison linéaire porte sur un nombre fini de termes, une famille infinie est libre si toute sous-famille finie est libre

La famille vide est linéairement indépendante. Un couple (u₁, u₂) de vecteurs est liée ss'il existe un scalaire tel que ou un scalaire tel que . Sous cette condition, les deux vecteurs u₁ et u₂ sont dits colinéaires. Si (u,v) est un couple de vecteurs libre, alors (u,v), (u+v,v) et (u,u+v) sont des couples de vecteurs non colinéaires, mais la famille (u,v,u+v) n'est pas libre pour autant.

Sous-espace vectoriel engendré

Le sous-espace vectoriel engendré par une famille , noté Span(v_i), est le plus petit sous-espace contenant tous les vecteurs de cette famille. De manière équivalente, c'est l'ensemble des combinaisons linéaires des vecteurs v_i. La famille engendre E, ou encore est génératrice, si E est le sous-espace vectoriel engendré.

Une base de E est une famille libre maximale ou, et c'est équivalent, une famille génératrice minimale. L'existence d'une base pour tout K-espace vectoriel E se déduit du théorème de la base incomplète et est équivalente à l'axiome du choix. Néanmoins, il existe des preuves spécifiques à la dimension finie. Une famille d'éléments de E est une base si et seulement si tout élément u de E s'exprime de manière unique comme combinaison linéaire des éléments de .

Définition de la dimension

Etant donné un espace vectoriel E sur un corps K, toutes les bases de E ont le même cardinal, appelé dimension de E. Si E admet une famille génératrice finie, alors la dimension est finie, et toutes les bases de E admettent le même nombre d de vecteurs, où d est la dimension de E.

• Le corps K est de dimension 1, une base étant donnée par l'unité 1_K. Tout espace vectoriel de dimension 1 est appelé droite vectorielle. Tout espace de dimension 2 est appelé plan vectoriel.
• A isomorphisme près, les espaces vectoriels sur K sont classifiés par leurs dimensions, ce qui rend cette notion fondamentale. La dimension de K^(A) est le cardinal de A. En particulier, la dimension de Kⁿ est n.
• En dimension finie, étant donnée une application linéaire f de E dans F, le théorème du rang permet de relier la dimension de l'image f(E) (appelée rang de f), la dimension du noyau de f et la dimension de E. En particulier, le rang de f est inférieur à l'infinimum des dimensions de E et de F, et cela reste vrai en dimension infinie

Pour tout sous-espace vectoriel V de E, on a : dim E = dim V + dim E/V.

Pour tous sous-espaces vectoriels U et W de E, on a :dim U + dim W = dim(U+W)+ dim (U∩W).

Propriétés des espaces vectoriels de dimension finie

Par ce qui précède, un espace vectoriel est de dimension finie ssi il est engendré par une partie finie. Soit E un espace vectoriel de dimension finie (non nulle) égale à n.

• Si F₁ et F₂ sont deux sous-espaces vectoriels de E, alors

.

Cette relation est connue sous le nom de formule de Grassmann.

• Si W est un sous-espace de E et que W et E ont même dimension, alors E=W
• Tous les supplémentaires d'un sous-espace vectoriel F de E ont la même dimension, qui est appelée codimension de F dans E.
• L'espace dual de E est également de dimension finie et de même dimension : .
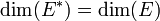• Soit 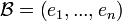une base de E.

Il existe une unique bas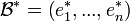e de 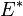telle que ,

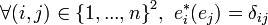où 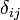est le symbole de Kronecker.

On dit alors que 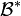est la base duale associée à .

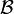• L'ensemble des formes n-linéaires alternées sur un espace vectoriel de dimension n est un espace vectoriel de dimension 1. Ce résultat est à la base de la théorie du déterminant.
• Le rang est la dimension de l'espace des colonnes, qui est égale à celle de l'espace des lignes

• Si E est de dimension finie, et que f est un opérateur sur E, alors f est injectif ssi f est surjectif ssi f est bijectif.