Division d'un polynôme - Définition

Introduction

En algèbre, l'anneau K[X] des polynôme à une indéterminée X et à coefficients dans un corps commutatif K, comme celui des nombres rationnels, réels ou complexes, dispose d'une division euclidienne, qui ressemble formellement à celle des nombres entiers. Si A et B sont deux polynômes de K[X], il existe un unique couple (Q, R) de polynômes de K[X] tel que :

Ici l'expression deg S, si S désigne un polynôme, signifie le degré de S. Cette division confère à l'ensemble des polynômes une arithmétique analogue à celle des nombres entiers, avec pour conséquence, l'identité de Bézout, le lemme d'Euclide ou encore un équivalent du théorème fondamental de l'arithmétique, où les nombres premiers sont remplacés par les polynômes unitaires irréductibles (cf l'article arithmétique des polynômes).

Il existe une deuxième division, dite selon les puissances croissantes. Elle est utilisée pour les fraction rationnelles et permet une décomposition en éléments simples.

Division euclidienne

Préambule

La division euclidienne dans un anneau de polynôme permet de construire à la règle et au compas l'heptadécagone, un polygone régulier de 17 côtés.

En 1801, Carl Friedrich Gauss publie son premier livre de mathématique, appelé Disquisitiones arithmeticae. Il démontre en particulier l'existence d'une nouvelle figure constructible à la règle et au compas, le polygone régulier à 17 côtés. La méthode qu'il utilise consiste à considérer un polynôme, non comme une fonction mais comme élément d'une structure, que l'on appelle maintenant anneau, doté d'une addition et d'une multiplication. Les éléments ne sont pas tous inversibles, rapprochant en cela cette structure de celle des nombres entiers. Cette analogie est rendue plus profonde si les coefficients des polynômes sont choisis dans un corps, c'est-à-dire un anneau tel que tous les éléments différents de 0 possèdent un inverse pour la multiplication. La structure dispose alors d'une division euclidienne à l'image de celle des entiers.

Sur un anneau commutatif, c'est-à-dire dont la multiplication est commutative, disposant d'une division euclidienne, on retrouve les résultats principaux de l'arithmétique élémentaire. Gauss s'exprime ainsi, en parlant de l'usage des techniques de la théorie algébrique des nombres (qu'il appelle arithmétique transcendante) pour les polynômes « ... n'appartient pas par elle-même à l'arithmétique, mais ses principes ne peuvent être tirés que de l'arithmétique transcendante. Ce résultat pourra sembler aussi inattendu que les vérités nouvelles qui en dérivent, et qu'il verront, j'espère, avec plaisir ».

Son objectif est de trouver les racines du polynôme cyclotomique, c'est-à-dire de la forme Xⁿ - 1,où n est un entier strictement positif. Comme Q[X] possède une structure analogue à celle des entiers, on y retrouve l'équivalent des nombres premiers, appelés ici facteurs irréductibles. Ce résultat se démontre exactement comme pour les nombres entiers. Ces facteurs portent le nom de polynômes cyclotomiques. La démonstration qu'il propose (et qui se trouve dans l'article associé) utilise un autre anneau de polynômes, sur le corps Z/pZ, où p désigne un nombre premier. Cette structure dispose encore d'une division euclidienne et donc d'une arithmétique analogue à celles nombres entiers.

Augustin Louis Cauchy utilise l'anneau C[X] où C désigne l'ensemble des nombres complexes pour présenter une démonstration du dernier théorème de Fermat en 1847. Si l'anneau utilisé est analogue à celui des nombres entiers, il dispose de quelques propriétés supplémentaires, cet tout élément inversible possède n racines n^ièmes de l'unité, ce qui lui permet de conclure et d'ouvrir une porte à de nouvelles méthodes de démonstrations.

Théorème et définitions

Dans le reste de l'article K désigne un corps commutatif, qui peut, par exemple être égal à Q celui des nombres rationnels, R celui des réels ou C celui des complexes. Le résultat principal du paragraphe découle d'un théorème :

Ce théorème est à l'origine de quelques définitions :

Le couple (Q, R) de l'identité de la division euclidienne n'est unique que si le degré de R est strictement plus petit que celui de Q. Si A est égal à X³ - X² + 1 et B à X², uniquement la première égalité correspond à celle de l'identité de la division euclidienne, la deuxième possèderait un reste de degré égal à celui de B :

Le degré, qui sert à définir la division euclidienne est appelé stathme (cf l'article Anneau euclidien).

La démonstration est généralement faite en deux temps. L'unicité est plutôt plus facile. Avec les notations du paragraphe précédent :

• Le couple (Q, R), s'il existe, est unique :

La démonstration se fonde sur une propriété des degrés, le degré du produit de deux polynômes M et N est égal à la somme des degrés de chaque polynôme :

On suppose l'existence de deux couples (Q₁, R₁), (Q₂, R₂) résultat de la division euclidienne de A par B, on va montrer qu'ils sont égaux. On dispose des égalités :

Si la différence entre Q₁ et Q₂ n'était pas nulle, le premier terme de la somme (1) serait au moins de degré de B, noté n. Comme R₁ et R₂ sont de degrés strictement inférieurs à n, le terme de gauche de l'égalité (1) ne pourrait être nulle. On en déduit que Q₁ et Q₂ sont égaux, l'égalité (1) montre alors que R₁ et R₂ sont aussi égaux.

• Il existe un couple (Q, R) satisfaisant l'identité de la division euclidienne :

Soient m et n les degrés de A et B. Les polynômes sont notés de la manière suivante :

Soit p  = m - n. Si p est strictement négatif, c'est-à-dire si n est strictement plus grand que m, il suffit de prendre Q égal au polynôme constant 0 et R égal à A pour établir l'existence. Raisonnons par récurrence pour établir les autres cas. Si p est égal à 0, c'est-à-dire si n est égal à m :

Ce qui démontre la proposition pour p égal à 0. Supposons maintenant la propriété démontrée pour toute valeur inférieure à p - 1 et montrons la pour p. Un calcul analogue au précédent montre l'existence d'un polynôme R₁ tel que :

La différence de degré entre R₁ et B est inférieure ou égal à p - 1, l'hypothèse de récurrence montre l'existence de deux polynômes Q₁ et R tel que :

En remplaçant la valeur de R₁calculée dans l'égalité (2) dans l'égalité (1), on obtient :

Ce qui établit la proposition.

 

Exemple et algorithme

La démonstration proposée pour montrer l'existence d'un couple satisfaisant l'identité de la division euclidienne offre aussi un algorithme de calcul, analogue à celui de la division euclidienne dans les entiers. Illustrons le sur un exemple, avec les notations précédentes :

Dans un premier temps, on calcule le couple de polynômes (P₁, R₁) de l'égalité (1). Le polynôme P₁ est un monôme égal à X³ et R₁ vérifie l'égalité :

Ce que l'on écrit :

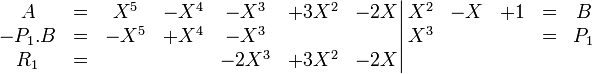
Le même calcul est effectué sur R₁ pour calculer le couple (P₂, R₂)

Ce qui permet de compléter :

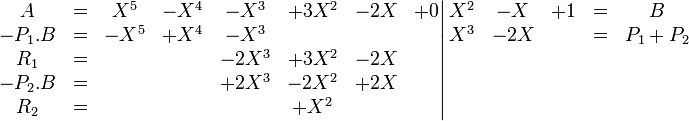
Une dernière étape permet de conclure :

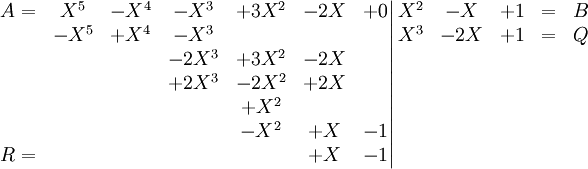
L'identité de la division euclidienne est maintenant établie :