Distance de Hausdorff - Définition

Introduction

Felix Hausdorff est le mathématicien à l'origine de la distance portant maintenant son nom.

En mathématiques, et plus précisément en géométrie, la distance de Hausdorff est un outil topologique qui mesure l’éloignement de deux sous-ensembles d’un espace métrique sous-jacent.

Cette distance apparait dans deux contextes bien différents. Pour le traitement d'images, elle est un outil aux propriétés multiples, source de nombreux algorithmes. Elle indique si deux formes sont les mêmes et, si elles sont différentes, la distance quantifie ces dissemblances. En dimension 2, la distance de Hausdorff permet de numériser une image ou encore de reconnaître une forme. Cet outil, issu des mathématiques pures, n'est pas toujours adapté pour les traitements industriels. Par exemple, deux formes aux contours de longueurs différentes peuvent être proches, au sens de cette distance. Pour ces raisons, on utilise parfois des variantes, comme la distance de Hausdorff modifiée.

Pour le mathématicien pur, cette distance est à la géométrie, ce que la norme de la convergence uniforme est à l'analyse. La convergence uniforme, en analyse fonctionnelle procède d'une démarche qui consiste à travailler sur un nouvel ensemble. On n'étudie plus le comportement des nombres, réels ou complexes, sur lesquels est définie la fonction, mais celui d'un ensemble de fonctions. Typiquement, on cherche à résoudre une question à l'aide d'une suite de fonctions, qui sont vues comme des points d'un vaste espace, et qui convergent vers la solution. Les séries de Fourier procèdent d'une démarche de cette nature. Il est tentant d'aborder un problème de géométrie de la même manière. Un point de l'espace devient un solide, on recherche à trouver une solution à l'aide d'une suite de solides convergeant vers la solution. La notion de convergence demande une topologie, celle induite par la distance de Hausdorff offre une réponse.

Un exemple d'application est le problème isopérimétrique dans le plan euclidien. La question est de savoir quelle est la surface de plus grande aire possible, pour un périmètre donnée, la réponse est le disque. Une méthode consiste à construire une suite, par exemple de polygones, qui converge vers la solution.

Les premières questions qui se posent sont un peu de même nature que celles de l'analyse fonctionnelle. Dans quel cas l'espace est complet, quels sont les compacts, dispose-t-on d'applications continues, existe-t-il des sous-espaces aisément manipulables et denses, un peu à l'image des polynômes ? Les réponses sont suffisamment positives pour que la démarche soit féconde. Si l'espace sous-jacent est complet, l'espace utilisant la distance de Hausdorff l'est aussi. Les compacts, si l'espace métrique est euclidien, sont des ensembles fermés bornés, les polygones forment un ensemble dense, enfin la somme de Minkowski est continue.

La richesse des théorèmes sont autant d'atouts pour la mise au point d'algorithmes spécifiques aux besoins de l'industrie.

Construction de la distance

Approche intuitive

Distance de Hausdorff entre deux ensembles C et D.

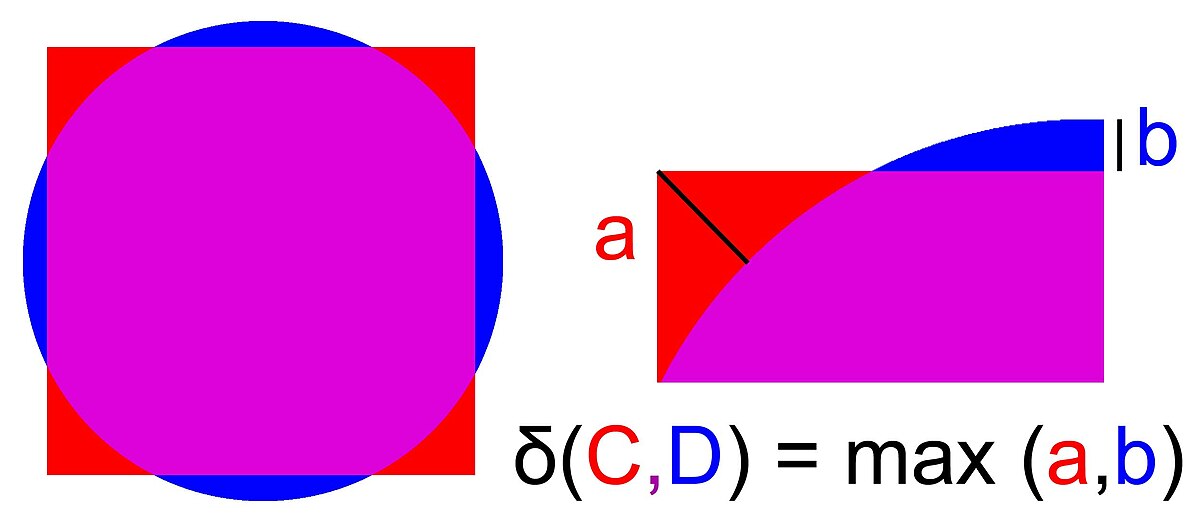
L'idée intuitive de Hausdorff est de définir la distance entre deux ensembles C et D comme indiqué sur la figure de droite. C représente le carré rouge et D le disque bleu de même surface et de même centre. A l'endroit où les deux figures coïncident la couleur est violette, sinon elle est bleue ou rouge. Les différences entre les deux figures se matérialisent sous la forme de 4 lunules bleues et 4 presque triangles rouges.

On considère le point du carré le plus éloigné du disque, c'est un sommet du carré, à une distance a du disque. On considère ensuite le point du disque le plus éloigné du carré, c'est le sommet de la lunule et sa distance au carré est notée b. La distance de Hausdorff est la plus grande valeur des deux, en l'occurrence a, pour l'exemple choisi. Les valeurs a et b sont parfois appelées distance de Hausdorff relative.

La distance de Hausdorff, pour l'ingénieur en imagerie, est un indicateur de similarité entre deux formes géométriques, c'est la raison même de son utilité.

Pour que cette distance puisse vérifier le premier axiome, c'est-à-dire celui indiquant que la distance entre deux figures distinctes n'est jamais nulle, on ne peut considérer tous les ensembles. Deux boules, une ouverte et l'autre fermée, de même centre et de même rayon seraient deux ensembles différents à une distance nulle. Une autre raison pousse à limiter les ensembles considérés. La distance entre une droite et une boule serait infinie, ce qui n'est pas possible d'après les axiomes de la distance. Pour cette raison, Hausdorff limite l'ensemble aux bornés. Cette distance est souvent utilisée pour étudier des géométries proches de celles d'un espace de dimension finie, pour cette raison, on impose parfois aux ensembles d'être compacts. Enfin, il n'est pas possible de donner un sens à la distance entre un fermé borné quelconque et l'ensemble vide, pour cette raison, l'ensemble vide n'est pas considéré.

Formulations de la distance

Il existe différentes manières d'exprimer la distance d(X, Y) entre deux ensembles fermés bornés non vides X et Y d'un espace métrique (E, δ). La première correspond à la définition du paragraphe précédent :

Une autre formulation consiste à considérer les ensembles X_r et Y_r, où r est un réel positif. Ici, X_r (resp. Y_r) désigne l'ensemble des points de E à une distance inférieure ou égale à r de X (resp. Y). La distance prend alors la forme suivante :

Enfin, il est possible de remarquer que l'ensemble X_r correspond à la somme de Minkowski de X et de r.B, si B désigne la boule unité fermée.

Définition formelle

Soient (E, δ) un espace métrique et E_H l'ensemble des fermés bornés de E non vides. La distance de Hausdorff d de E_H est l'application de E_HxE_H dans R₊ définie par :

Ces notations sont utilisées dans tout le reste de l'article.

Remarque : Il est utile de bien séparer la distance d de celle de δ. On remarque en effet que la distance entre le vecteur nul et B est égale à 0, en revanche, la distance de Hausdorff entre le singleton vecteur nul et B est égal à 1.

Si la distance sur E est bornée, la distance de Hausdorff peut même être étendue à l'ensemble des sous-espaces fermés (non nécessairement compacts) de E. Dans le cas contraire, la « distance » ainsi définie peut prendre des valeurs infinies.

Il est également possible de définir la distance de Hausdorff entre deux sous-ensembles non fermés de E comme la distance de Hausdorff entre leur adhérence. On munit ainsi l’ensemble des sous-ensembles de E d’une pseudo-métrique (puisque deux sous-ensembles distincts mais partageant la même adhérence auront une distance de Hausdorff nulle).