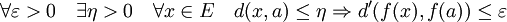Continuité - Définition
La liste des auteurs de cet article est disponible ici.
Définition générale (espaces topologiques)
On donne deux définitions équivalentes dans le cas des espaces topologiques.
Définition locale
La définition locale (c'est-à-dire pour un point) de la continuité repose sur la notion mathématique de limite. Une fonction sera dite continue en un point a si sa limite en a est égale à sa valeur en a.
La notion de seuil utilisée pour les fonctions réelles est généralisée par la notion de voisinage : 
désigne l'ensemble des voisinages de a, et 
ceux de f(a).
Définition — Soient E et F deux espaces topologiques, 
et 
.
La fonction f est dite continue en a si :
ou plus simplement :
ce qui équivaut aussi à :
- pour tout ouvert O contenant f(a),
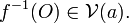
Ainsi f est continue au point 
si et seulement si :
La fonction f est dite continue (tout court, ou continue sur 
) si et seulement si elle est continue en tout point de .
La fonction f est dite continue sur une partie 
de si et seulement si elle est continue en tout point de .
Caractérisations globales
On peut déduire de la définition locale trois caractérisations équivalentes des applications qui sont continues en tout point de l'espace de départ.
La première d'entre elles est qu'une application est continue (en tout point) si et seulement si l'image réciproque de tout ouvert de l'espace d'arrivée est un ouvert de l'espace de départ. La deuxième, analogue, s'écrit en termes de fermés. La troisième utilise les notions d'adhérence et d'image directe.
Le lien avec la notion intuitive est le suivant : quand une fonction « saute », cela signifie que des points très proches de l'espace de départ, se retrouvent sur des points très éloignés à l'arrivée. Or pour une application continue, ces sauts sont impossibles, car si on considère un point du départ et son image à l'arrivée, on sait que tout un voisinage de ce point de départ doit arriver au voisinage du point d'arrivée !
Théorème — Soient E et F deux espaces topologiques. Une application est continue en tout point de E si et seulement si elle vérifie l'une des trois propriétés équivalentes suivantes :
- pour tout ouvert O de F,
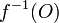est un ouvert de E ; - pour tout fermé G de F,
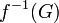est un fermé de E ; - pour toute partie A de E ,
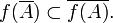
- f est continue en tout point ssi elle vérifie la propriété 1 :
D'après la définition locale, f est continue en a ssi pour tout ouvert O de F tel que a appartienne à f -1(O), f -1(O) est voisinage de a. Donc f est continue en tout point ssi pour tout ouvert O de F, f -1(O) est voisinage de chacun de ses points, c'est-à-dire est ouvert.
- f vérifie la propriété 1 ssi elle vérifie la 2 :
Par passage aux complémentaires.
- f vérifie la propriété 2 ssi elle vérifie la 3 :
La propriété 3 équivaut à : tout fermé contenant f(A) contient 
, ou encore : pour tout fermé G et toute partie A de f -1(G), 
, ce qui se simplifie en : pour tout fermé G et pour A=f -1(G), 
, qui équivaut à la propriété 2.
- Les caractérisations 1 et 2 sont souvent utilisées, a contrario, pour montrer qu'un certain ensemble est ouvert (ou fermé) en faisant intervenir une application qu'on sait déjà être continue. Par exemple l'hyperbole
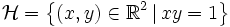peut être vue comme l'image réciproque de 
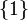par l'application produit :
L'hyperbole 
est fermée car elle est l'image réciproque du singleton par l'application continue 
.
- Ce théorème permet de montrer que si E est une réunion d'ouverts tels que la restriction de f à chacun de ces ouverts soit continue alors f est continue, et de même si E est réunion d'un nombre fini de fermés tels que la restriction de f à chacun de ces fermés soit continue. Pour une réunion (même finie) de parties "quelconques" on n'a aucun résultat de ce genre.
Équivalence de la définition métrique et topologique
Un espace métrique 
possède une topologie associée 
. Un ouvert de est un ensemble tel que pour tout point de l'ouvert, il existe une boule ouverte non vide et de centre le point incluse dans l'ouvert :
Un voisinage 
de est un sous-ensemble contenant un ouvert contenant . Par conséquent il existe une boule ouverte non vide de centre et incluse dans
Les deux définitions de la continuité d'une fonction par la topologie sont équivalentes. Si 
désigne la topologie associée à un espace métrique 
, alors :
Propriété — La fonction 
de dans est continue en un point 
de 
si et seulement si elle est continue en ce point, considérée comme une fonction de 
dans 
.
En effet, la fonction est continue en du point de vue topologique si et seulement si :
Par construction de la topologie, cette condition s'exprime :
La dernière définition correspond exactement à celle de la continuité formalisée par les distances.