Variable aléatoire - Définition
le résultat du jet d'un dé
Une variable aléatoire est une fonction définie sur l'ensemble des résultats possibles d'une expérience aléatoire, telle qu'il soit possible de déterminer la probabilité pour qu'elle prenne une valeur donnée ou qu'elle prenne une valeur dans un intervalle donné. À l'origine, une variable était une fonction de gain, qui représentait le gain obtenu à l'issue du résultat d'un jeu. Par exemple, supposons qu'un joueur lance un dé et que celui-ci gagne 1€ s'il amène un six et perde 10€ s'il amène un autre résultat. Alors il est possible de définir la variable aléatoire de gain qui associe 1 au résultat " six " et -10 à un résultat inintéressant. La probabilité pour que la variable aléatoire prenne la valeur 1 correspond exactement à la probabilité pour que le joueur gagne 1€. Les variables aléatoires sont très utilisées en théorie des probabilités et en statistiques. Dans les applications, les variables aléatoires sont utilisées pour modéliser le résultat d'un mécanisme non-déterministe ou encore comme le résultat d'une expérience non-déterministe qui génère un résultat aléatoire.
Détails
- La variable aléatoire la plus simple est donnée par le résultat d'un lancer au jeu de pile ou face, qui vaut pile ou face. Un autre exemple simple est donné par le résultat d'un jet de dés, pour lequel les valeurs possibles sont 1, 2, 3, 4, 5, 6 (si le dé est classiquement cubique). De telles variables aléatoires sont qualifiées de discrètes car elles prennent des valeurs bien séparées. A contrario, la mesure de la taille d'un individu pris au hasard dans une population ressemble davantage à un nombre réel positif (cela n'est pas tout à fait vrai non plus, car des questions ergonomiques rendent d'autant plus improbable l'énoncé d'un nombre qu'il comporte de décimales significatives; l'attracteur est en fait un fractal). Cette variable aléatoire est alors qualifiée par convention de continue. L'étude de la répartition des valeurs prises par une variable aléatoire conduit à la notion de loi de probabilité.
- En mathématiques, et plus précisément en théorie des probabilités, une variable aléatoire est une fonction mesurable définie sur un espace de probabilités. La mesure image correspondante est appelée loi de la variable aléatoire. Ce type de fonction permet de modéliser un phénomène aléatoire, comme par exemple le résultat d'un jet de dés. Une propriété intéressante de l'intégrale de Lebesgue fait qu'un évènement de probabilité strictement nulle n'est pas nécessairement impossible au sens strict du terme (ainsi, considérons un réel tiré au hasard dans l'intervalle [0, 1] ; la probabilité qu'il soit rationnel est nulle, alors que les rationnels constituent dans cet intervalle un ensemble infini, et même partout dense).
Quelques variables aléatoires
En guise d'introduction aux définitions concernant les variables aléatoires, il semble intéressant de présenter brièvement une famille de variables très utilisées.
Outre la variable certaine qui prend une valeur donnée avec une probabilité égale à 1, la variable aléatoire la plus simple est appelée variable de Bernoulli. Celle-ci peut prendre deux états, qu'il est toujours possible de coder 1 et 0, avec les probabilités p et 1-p. Une interprétation simple concerne un jeu de dé dans lequel on gagnerait un euro en tirant le six (p = 1/6). Sur une séquence de parties, la moyenne des gains tend vers p lorsque le nombre de parties tend vers l'infini.
Si on considère qu'une partie est constituée par n tirages au lieu d'un seul, le total des gains est une réalisation d'une variable binomiale qui peut prendre toutes les valeurs entières de 0 à n. Cette variable a pour moyenne le produit np. On obtient un exemple moins futile en considérant le score d'un candidat dans un sondage électoral.
Si n est assez grand et p pas trop petit, on peut trouver une approximation convenable en utilisant la variable de Gauss. Dans les sondages cela permet d'associer un intervalle de confiance au résultat brut. Ainsi, il y a 95 chances sur 100 pour qu'une enquête portant sur 1 000 personnes donne un résultat correct à ± 3 % près.
Toujours avec n grand, l'approximation de Poisson est préférable si p est assez petit pour que la moyenne np ne soit pas trop grande, de l'ordre de quelques unités. Dans un sondage ce serait la loi applicable aux " petits " candidats. C'est surtout la loi utilisée dans des problèmes de files d'attente.
La somme des carrés de ν variables de Gauss indépendantes est une variable de χ2 à ν degrés de liberté (la variable exponentielle en est un cas particulier). Le test du χ2 est utilisé pour apprécier la valeur de l'adéquation d'une loi de probabilité sur une distribution empirique.
Si on divise une variable de Gauss par une variable de χ (racine carrée de la précédente), on obtient une variable de Student. Le rapport de deux variables de χ2 indépendantes définit une variable de Snedecor. Ces deux lois sont utilisées dans l'analyse de populations supposées gaussiennes.
Notions de base
Fonction de répartition
Il serait possible d'introduire cette notion à partir de l'une quelconque des variables précédemment considérées mais il paraît plus clair d'étudier le cas du dé sous un angle différent. En effet, il définit une variable aléatoire X qui prend avec la même probabilité d'apparition (1/6) des valeurs dans l'ensemble {1,2,3,4,5,6}. On peut alors associer à toute valeur réelle x la probabilité d'obtenir un tirage inférieur ou égal à x, ce qui définit une courbe en escalier dont les marches ont une hauteur égale à 1/6.
Formellement, cela conduit à une fonction de répartition
Dans celle-ci, la majuscule X représente la variable aléatoire, ensemble de valeurs numériques, et la minuscule x représente la variable d'état, variable au sens usuel du terme.
Si les événements ne sont plus équiprobables, cela ne fait que déformer la courbe. Pour introduire une notion nouvelle, on peut commencer par remplacer le dé par une roulette à six numéros, ce qui conduit à un problème rigoureusement identique. Ensuite, on ne change rien de fondamental si on remplace les six nombres entiers par les repères des centres d'arcs de 60 degrés. À partir de là il est possible d'augmenter le nombre de secteurs en réduisant leur taille : les échelons deviendront de plus en plus petits jusqu'à être indiscernables sur un dessin. Le passage à la limite remplace la variable discrète par une variable continue qui prend toutes les valeurs réelles dans l'intervalle ]0,360] : c'est une variable uniforme.
Une fonction de répartition est croissante (au sens large) sur l'intervalle ]-∞,+∞[, et continue à droite en tout point ; elle tend vers 0 en -∞ et vers 1 en +∞. Réciproquement, toute fonction vérifiant les propriétés (caractéristiques) précédentes peut être considérée comme la fonction de répartition d'une variable aléatoire.
L'intérêt de la fonction de répartition réside dans le fait qu'elle est valable aussi bien pour les variables continues définies sur un ensemble continu que pour les variables discrètes définies sur un ensemble dénombrable (dans la plupart des cas pratiques il se réduit à un ensemble de valeurs équidistantes que l'on peut ramener à un ensemble d'entiers). Le remplacement progressif de courbes en escaliers par des courbes continues permet de voir intuitivement comment une variable continue peut fournir une approximation souvent plus facile à manipuler que la variable discrète originale.
Malheureusement ces avantages de la fonction de répartition, intéressants pour la visualisation des phénomènes, disparaissent dès que l'on veut approfondir les problèmes. Dans ce cas, il est généralement plus commode d'utiliser les notions décrites dans les paragraphes suivants.
Fonction de probabilité d'une variable discrète
La loi d'une variable discrète est déterminée tout simplement par l'ensemble des probabilités de ses valeurs (Fonction de Masse). Si l'on suppose qu'elle prend des valeurs entières (de signe quelconque), cela s'écrit :
On reconstruit la fonction de répartition (dont les valeurs sont alors appelées probabilités cumulées) par la relation :
si 
, alors 
.
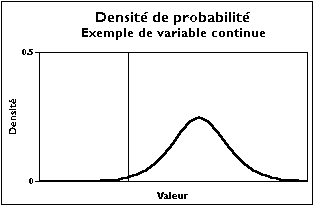
Densité de probabilité d'une variable continue
Une variable continue possède en général une fonction de répartition continue en tout point et dérivable par morceaux. Il est alors commode de la dériver pour obtenir la densité de probabilité, vérifiant :
qui est définie et à valeurs positives (ou nulles) sur ![]-\infty,\, +\infty[\,](https://static.techno-science.net/illustration/Definitions/autres/d/d278f0180705c10ffa73acbea25f0949_6252211f3071d6a6994aa2b877050774.png){kind=small}
, telle que 
.
On reconstruit la fonction de répartition par la relation :
Dans les raisonnements généraux, il est souvent commode d'écrire ces formules sous forme différentielle :
Si l'on effectue un changement de variable selon la formule 
, la nouvelle densité de probabilité se calcule par :
Espérances mathématiques
Définition
L'espérance mathématique d'une variable aléatoire se définit comme la moyenne des valeurs prises par cette variable, pondérées par leurs probabilités.
Dans le cas d'une variable discrète que l'on suppose prendre les valeurs entières, elle se définit simplement par
![E[X] = \sum_{k=-\infty}^{+\infty} k\ P_X(k)](https://static.techno-science.net/illustration/Definitions/autres/1/1ce3a97f6498a2af336bb19cd6b7940e_5d1a6aeffed3676589e3d6c9c032477c.png)
(sous réserve d'existence, c'est-à-dire ici de sommabilité).
Pour une variable continue, la formule différentielle donnée précédemment s'intègre en
![E[X] = \int_{-\infty}^{+\infty} x\ p_X(x)\ dx](https://static.techno-science.net/illustration/Definitions/autres/9/9124b0df7a544ee2165b6cb3360c998e_b99913a871850442b9b6393d59d8d69f.png){kind=small}
(sous réserve d'existence, c'est-à-dire ici d'intégrabilité).
Généralisation
X étant une variable aléatoire, une fonction f supposée régulière définit une nouvelle variable aléatoire f(X) dont l'espérance, lorsqu'elle existe, s'écrit en remplaçant k par f(k) ou x par f(x) dans les formules précédentes (théorème de transfert).
En particulier, il est intéressant de considérer la variable aléatoire à valeurs complexes 
(où 
) dont l'espérance mathématique est [la valeur en θ de] la transformée de Fourier inverse de la densité de probabilité :
![\phi_X(\theta) = E\left[e^{i \theta X}\right]\,](https://static.techno-science.net/illustration/Definitions/autres/c/ccbcdf091c03b47410ff4b219fa03b85_237f5f89b2c61c9142600ba0d2c18eee.png){kind=small}
L'exponentielle se développe en série :
![\phi_X(\theta) = E\left[\sum_{k=0}^\infty {(i \theta X)^k \over {k !}}\right]](https://static.techno-science.net/illustration/Definitions/autres/2/26c9f766659c386084ab0fedb80c8c23_19f81213437d1b196708a115e5fa8369.png)
ou, si la densité de probabilité est une fonction suffisamment régulière :
![\phi_X(\theta) = \sum_{k=0}^\infty {(i \theta)^k \over {k !}}E\left[X^k\right]](https://static.techno-science.net/illustration/Definitions/autres/6/6a4d8114cf9ab7b05b354ceeaacde15b_7425d680a129710faec2fa9c6713eafb.png)
Moments par rapport à l'origine
Les quantités ![E\left[X^k\right]\,](https://static.techno-science.net/illustration/Definitions/autres/e/ecf2465088771d6e7f8b06afd6afaec7_f9a8ebfd3b535c7085ba295fe8883ce0.png){kind=small}
sont appelées les moments par rapport à l'origine (moments ordinaires ou raw moments en anglais) de la variable aléatoire X et sont généralement notées :
![m_k(X) = E\left[X^k\right]\,](https://static.techno-science.net/illustration/Definitions/autres/d/d9adfab1c9fa8df5b04946eedd982dad_9ad4096867bd59e875de9b6ee1dcfb6d.png){kind=small}
.
Une variable aléatoire suffisamment régulière peut être caractérisée, et de façon équivalente, par sa fonction de répartition, sa densité de probabilité (ou sa fonction de probabilité), sa fonction caractéristique ou la suite de ses moments 
.
Moments centrés
Le moment d'ordre 1 par rapport à l'origine, ![m_1(X) = E[X]\,](https://static.techno-science.net/illustration/Definitions/autres/7/79e4ff7e54cf0f4017122dacc54fe73f_ffc5ce4218c4c27a256097b908757751.png){kind=small}
, souvent noté 
, représente la moyenne, valeur centrale.
En ce qui concerne les moments d'ordre supérieur, il est souvent plus commode d'utiliser, plutôt que les moments par rapport à l'origine , les moments centrés, notés généralement 
et qui se définissent ainsi :
![\mu_k(X) = E[(X-\overline X)^k],](https://static.techno-science.net/illustration/Definitions/autres/7/73522404137916b381410707240ce5a4_438fa50eebadf1c85031f7d19747d6f2.png){kind=small}
Le plus utile de ces moments est la variance, valeur de dispersion :
![\sigma_X^2 = E[(X-\overline X)^2] = E[X^2] - (E[X])^2 = \overline {X^2} -(\overline X)^2](https://static.techno-science.net/illustration/Definitions/autres/8/8d12e448c47fc04436a1447f5414830c_412c618335dd608fbb7675461a6eeff7.png){kind=small}
dont la racine carrée fournit une grandeur homogène à la grandeur de base et à la moyenne, et appelée écart-type de la variable aléatoire X : σX.
Il existe des formules (qui ressemblent à celle du binôme) permettant de calculer un moment centré d'ordre k à partir des moments ordinaires d'ordre inférieur ou égal à k, et réciproquement ; voici quelques exemples (jusqu'à l'ordre 4) :
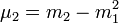
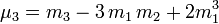
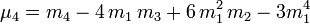
- et :
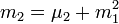
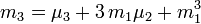
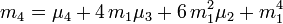
Médiane
On appelle médiane d'une variable aléatoire X, un réel m tel que
Dans le cas d'une variable aléatoire discrète, cette définition est peu intéressante car elle permet l'existence de plusieurs médianes
- si X est le numéro apparaissant sur la face supérieure d'un dé à 6 faces parfaitement équilibré, pour tout réel m strictement compris entre 3 et 4, on a :
ou bien l'existence d'une médiane qui ne donne pas une probabilité de 0,5
- Si X est la somme obtenue en lançant deux dés à 6 faces parfaitement équilibrés. X ne possède qu'une seule médiane 7 mais
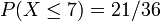
Dans le cas d'une variable continue, si la fonction de répartition est strictement croissante, la définition est équivalente à la suivante :
- la médiane de X est le réel unique m tel que
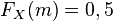
Le fait que la fonction de répartition soit continue, et supposée strictement croissante, à valeurs dans ]0 ; 1[, assure l'existence et l'unicité de la médiane.
Informatique
On utilise souvent des générateurs pseudo aléatoires pour simuler le hasard. Il existe également des moyens d'exploiter l'indétermination de phénomènes physiques, par exemple en analysant les variations d'un film de lampe à lave, ou en analysant le bruit thermique.