Isométrie - Définition
En géométrie, une isométrie est une transformation qui conserve les longueurs. Une isométrie est donc un cas particulier de similitude.
Si cette isométrie conserve aussi les angles orientés, alors ils s'agit d'un déplacement. Si elle inverse les angles orientés, il s'agit d'un antidéplacement.
Le terme isométrie est parfois un peu vague. Usuellement, il renvoie aux isométries affines, c’est-à-dire aux transformations bijectives d'un espace affine euclidien dans un autre qui conseve les distances. On généralise au tranformations bijectives d'un espace métrique dans un autre qui conserve les distances. Dans un cadre linéaire, on parle parfois d'isométrie vectorielle, c’est-à-dire d'automorphisme qui conserve le produit scalaire, mais il est plus prudent dans ce cadre de parler d'automorphisme orthogonal.
Isométries planes remarquables
On désigne par 
le plan (i.e., plus précisément, un plan affine réel euclidien orienté). Les applications suivantes sont des isométries de :
- Étant donné un vecteur
l'application qui, à tout point A, associe le point A' tel que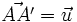 
: c'est la translation de vecteur . Sa réciproque est la translation de vecteur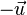 
. Elle n'a aucun point fixe, sauf si 
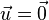, auquel cas c'est l'identité. Les translations sont des déplacements. - Étant donnée une droite Δ l'application qui, à tout point A, associe le point A' tel que
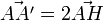, où H est le projeté orthogonal de A sur Δ: c'est la réflexion d'axe Δ. On peut la définir autrement: A' = A si 
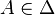et, si 
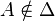, A' est tel que Δ est la médiatrice de [AA']. Les réflexions sont involutives et sont des antidéplacements. - Étant donné un point A de 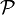et un réel θ l'application qui fixe A et, à un point B distinct de A, associe l'unique point B' tel que AB = AB' et une mesure de l'angle orienté
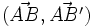est θ: c'est la rotation de centre A et d'angle θ. La réciproque de la rotation de centre A et d'angle θ est la rotation de centre A et d'angle − θ. Enfin, les rotations sont des déplacements.
Classification des isométries planes ayant un point fixe
- Une isométrie du plan ayant trois points fixes non alignés est l'identité.
- Une isométrie du plan autre que l'identité ayant au moins deux points fixes A et B est la réflexion par rapport à la droite (AB).
- Une isométrie du plan ayant un unique point fixe A est une rotation de centre A.
- Soit f une isométrie plane autre que l'identité. Soit M un point du plan et M' = f(M) tel que
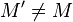. Un point fixe A de f vérifie MA = M'A donc est sur la médiatrice de [MM']: les points fixes sont donc alignés. Par contraposée, si f a trois points fixes non alignés, c'est l'identité. - Soit f une isométrie plane autre que l'identité ayant au moins deux points fixes A et B et s la réflexion par rapport à la droite (AB). Soit C un point n'appartenant pas à (AB). Alors son image C' par f vérifie CA = C'A et CB = C'B donc C' appartient à l'intersection de deux cercles de centres respectifs A et B. Cette intersection a au plus deux points et C' est différent de C (sinon f aurait trois points fixes non alignés et serait l'identité, ce qui est exclu par hypothèse) donc C et C' sont les deux points d'intersection respectifs de ces cercles (rappelons que deux cercles de centres distincts ont au plus deux points en commun). Comme CA = C'A et CB = C'B, A et B sont sur la médiatrice de [CC']; par définition, on a donc s(C') = C. Comme s(A) = A et s(B) = B,
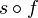a trois points fixes non alignés (à savoir A, B et C), donc 
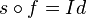. On a donc f = s − 1, i.e. f = s (car les réflexions sont involutives. f est donc la réflexion par rapport à la droite (AB). - Si f possède un unique point fixe A: soit B un point distinct de A et B' = f(B). On a alors
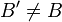. Soit Δ la médiatrice de [BB'] et s la réflexion par rapport à la droite Δ. D'une part, BA = B'A, donc 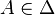et s(A) = A; d'autre part, s(B') = B. L'application 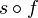possède donc au moints deux points fixes: A et B. 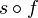est donc soit l'identité soit une réflexion. On ne peut avoir 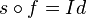, car sinon f=s aurait une infinité de points fixes (tous les points de Δ). 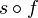est donc une réflexion s' par rapport à une droite passant par A (car s(f(A)) = A). On a donc 
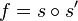et f est donc une rotation car composée de deux réflexions d'axes sécants.