Forme linéaire - Définition

En algèbre linéaire, les formes linéaires désignent un type particulier d'applications linéaires. L'étude spécifique qu'on leur accorde est motivée par le fait qu'elles jouent un rôle primordial en mathématiques, et en analyse, par exemple dans la théorie des distributions, ou dans la théorie des espaces de Hilbert.

Définition

En algèbre linéaire, une forme linéaire sur un espace vectoriel est une application linéaire définie sur et à valeurs dans son propre corps de base.

En d'autres termes, étant un - espace vectoriel, on dit que l'application de dans est une forme linéaire si :

.

Remarques

• L'ensemble des formes linéaires sur 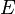est lui-même un 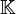- espace vectoriel. On l'appelle le dual de 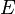et il est noté .
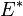• L'application constante de valeur 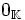s'appelle la " forme linéaire nulle ".

Exemples

est une forme linéaire sur

• Si L¹(Ω) est le -espace vectoriel des fonctions à valeurs complexes intégrables sur l'espace mesuré Ω alors l'intégrale est une forme linéaire sur L¹(Ω). Cela signifie que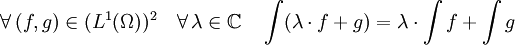

Base duales et antéduales

L'ensemble des formes linéaires sur un espace vectoriel se note en général et s'appelle l'espace vectoriel dual de , ou plus simplement son espace dual. Si est de dimension finie , il est remarquable que soit aussi de dimension finie . En d'autres termes, on peut aussi dire qu'un espace de dimension finie est isomorphe à son dual. Cependant, il n'y a pas d'isomorphisme canonique dans le sens où si est quelconque, il est nécessaire de se donner une base arbitraire afin de pouvoir définir un isomorphisme le reliant à . Si une base de , on définit sur celle-ci les formes linéaires notées par :

(où δ_ij est le symbole de Kronecker, c'est-à-dire valant 1 si i = j et 0 sinon). Ces formes linéaires sont aussi appelées les projections des coordonnées, l'image d'un vecteur x par n'est autre que la i-ème coordonnée du vecteur x dans la base . Le résultat important est que la famille de formes linéaires forme une base de E ^* ; on appelle aussi cette base la base duale de la base .

Inversement, si on se donne une base de , il existe une unique base de telle que:

La base s'appelle la base antéduale de la base .

Propriétés algébriques

• Si 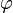est une forme linéaire non nulle, alors elle est surjective  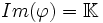: , où 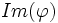est l'image de .
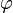• Si 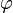est une forme linéaire non nulle, alors son noyau  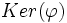est un hyperplan de .
  

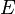Réciproquement, si 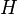est un hyperplan de 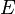, il existe une forme linéaire 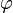telle que  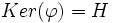; cette forme linéaire (nécessairement non nulle) est unique, à un coefficient multiplicatif non nul près.

• Enfin, une propriété importante est que deux formes linéaires ont le même noyau si et seulement si elles sont proportionnelles.

Formes linéaires continues

Si on considère un espace vectoriel normé sur le corps ou , alors on sait définir la notion de continuité de n'importe quelle application linéaire et en particulier, on dispose d'une notion de continuité pour les formes linéaires.

• Si 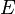est un espace vectoriel normé et 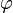est une forme linéaire continue alors elle est uniformément continue.

Formes linéaires continues sur un espace de Hilbert

On suppose désormais que est un espace de Hilbert sur le corps et on note le produit scalaire sur cet espace vectoriel.

On démontre que les formes linéaires continues sur s'expriment alors toutes d'une manière simple en fonction du produit scalaire et plus précisément :

.

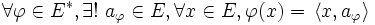Grâce à Riesz.