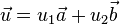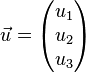Vecteur - Définition

Approche algébrique

Coordonnées et vecteurs colonnes

Dans un plan, deux vecteurs et non nuls et de directions différentes possèdent une propriété importante. Un vecteur quelconque est somme d'un multiple de et . Cela signifie qu'il existe deux uniques nombres u₁ et u₂ tel que :

est alors qualifié de combinaison linéaire de et . Comme tout vecteur du plan s'exprime de manière unique comme combinaison linéaire de et , la famille ( , ) est qualifiée de base du plan et u₁, u₂ sont appelés composantes du vecteur dans cette base. Cette définition correspond à celle d'un plan affine muni d'un repère. Une telle propriété est encore vraie dans l'espace. Cependant, deux vecteurs ne suffisent plus, toute base contient exactement trois vecteurs non nuls et dont les directions ne sont pas coplanaires (c'est-à-dire qu'il n'existe aucun plan contenant les trois directions). Si dans l'espace, les trois composantes d'un vecteur sont u₁, u₂ et u₃, il est d'usage de noter :

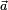
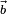
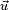
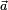
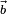
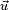
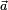
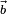
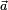
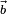
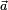
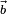
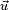
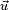
pour indiquer les composantes du vecteur. Le tableau est appelé vecteur-colonne et correspond à un cas particulier de matrice. Les opérations algébriques sur les vecteurs sont simples, avec une telle représentation. Additionner deux vecteurs revient à additionner chacune des composantes et la multiplication par un scalaire revient à multiplier chaque composante par le scalaire.

Dans un plan vectoriel, un vecteur s'identifie à un couple de scalaires, et dans l'espace à un triplet. Si les nombres choisis sont réels alors un plan (respectivement un espace) s'identifie à R² (respectivement à R³). Ici, R désigne l'ensemble des nombres réels.

Ébauche d'une construction algébrique

La logique précédente, appliquée pour une dimension égale à deux ou trois se généralise. Il est ainsi possible de considérer la structure Rⁿ où de manière plus générale Kⁿ avec K un ensemble de scalaires possédant de bonnes propriétés (précisément, K est un corps commutatif). Une telle structure possède une addition, et une multiplication par un scalaire définies comme au paragraphe précédent.

Il est possible de généraliser encore la définition d'un vecteur. Si un ensemble E possède une addition et une multiplication scalaire sur un corps commutatif et si ses opérations vérifient certaines propriétés, appelées axiomes et décrites dans l'article détaillé, alors E est appelé espace vectoriel et un élément de E vecteur.

De très nombreux exemples d'ensembles mathématiquement intéressants possèdent une telle structure. C’est le cas par exemple des espaces de polynômes, de fonctions vérifiant certaines propriétés de régularité, de matrices... Tous ces ensembles peuvent alors être étudiés avec les outils du calcul vectoriel et de l'algèbre linéaire.

La notion de dimension fournit le premier résultat de classification concernant les espaces vectoriels. Dans un espace vectoriel de dimension finie n, il est possible, moyennant le choix d'une base, de se ramener au calcul sur des vecteurs colonnes de taille n. Il existe également des espaces vectoriels de dimension infinie. L'ensemble des fonctions de R dans R est ainsi un espace vectoriel sur le corps des nombres réels, de dimension infinie. Vue sous cet angle, une telle fonction est un vecteur.

Construction algébrique et géométrie

Si les deux constructions, algébrique et géométrique sont équivalentes pour les structures vectorielles du plan et de l'espace usuel, la géométrie apporte en plus les notions de distance et d'angle.

La notion de produit scalaire permet de combler cette lacune. Un produit scalaire associe à deux vecteurs un réel. Si les deux vecteurs sont identiques le réel est positif. Il existe un produit scalaire tel que la norme du vecteur soit égale à la racine carrée du produit scalaire du vecteur avec lui-même. La géométrie euclidienne apparait alors comme l'étude d'un espace affine comprenant un espace vectoriel de dimension deux ou trois sur le corps des réels, muni d'un produit scalaire : plan affine euclidien ou espace affine euclidien.

Une fois équipée d'un produit scalaire, il devient possible de définir sur l'espace vectoriel des transformations classiques de géométrie euclidienne comme la symétrie, la rotation ou la projection orthogonale. La transformation associée aux espaces vectoriels laisse toujours invariant le vecteur nul. Les rotations permettent de définir la notion d'angle pour les vecteurs. L'angle est égal à si et seulement s'il existe une rotation qui envoie sur et sur . Cette définition, qui s'applique à une formalisation algébrique de la notion d'espace vectoriel, est équivalente à celle de la construction géométrique. Une telle approche simplifie parfois grandement les démonstrations, un exemple est le théorème de Pythagore.

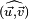
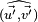
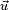
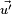
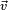
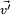
L'approche algébrique permet de définir toutes les notions de la géométrie euclidienne, elle généralise cette géométrie à une dimension quelconque si les nombres sont réels. Dans le cas des nombres complexes une construction analogue, appelée espace hermitien, existe.