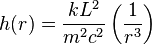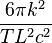Vecteur de Runge-Lenz - Définition
La liste des auteurs de cet article est disponible ici.
Hodographes circulaires de la quantité de mouvement
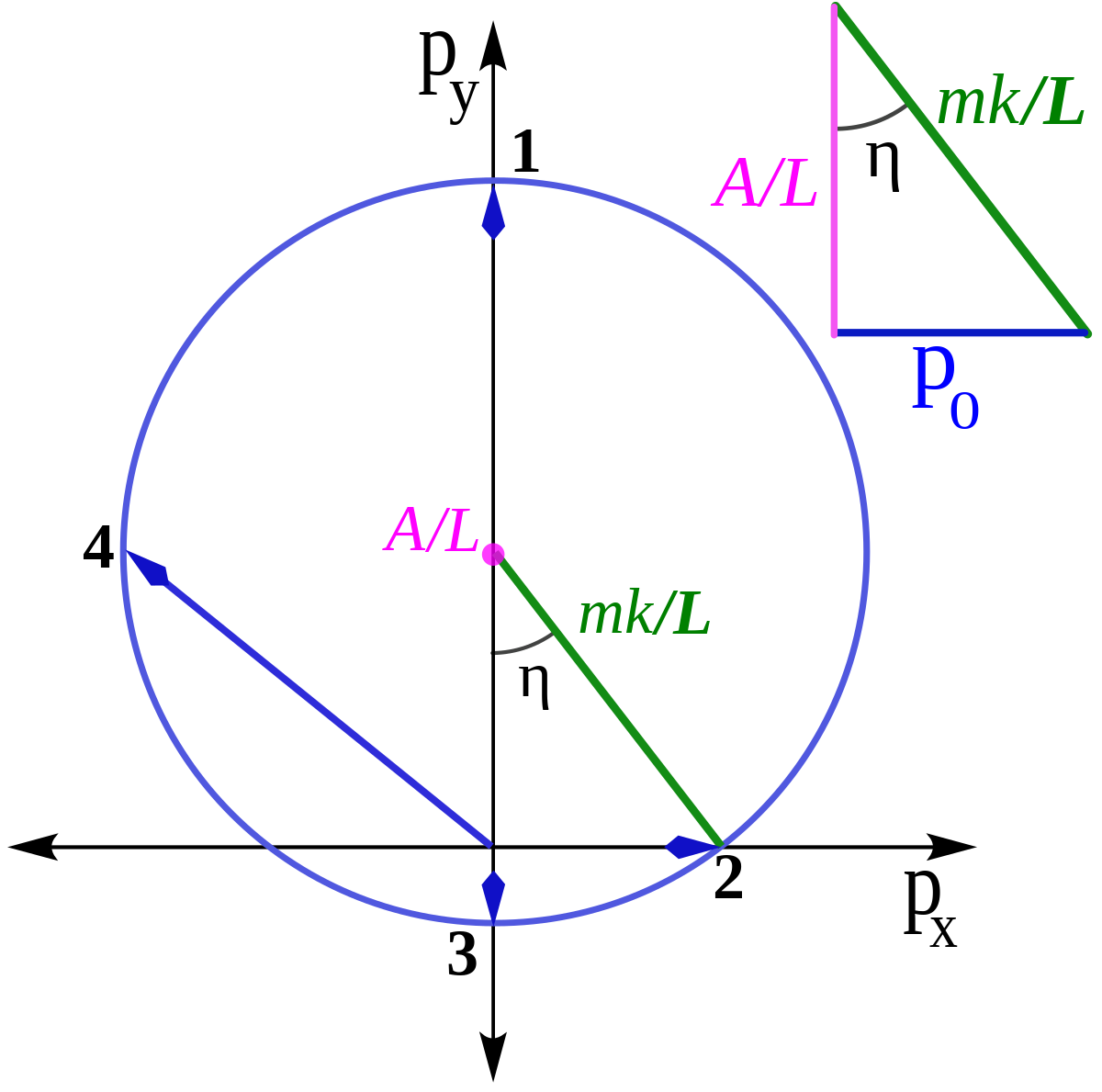
La conservation du vecteur de Runge-Lenz A et du vecteur moment cinétique L est utile pour montrer que le vecteur p se déplace sur un cercle dans un mouvement à force centrale suivant une loi en carré inverse. Le produit vectoriel de A et L mène à une équation pour p
En prenant L le long de l'axe z et le grand-axe suivant l'axe x on obtient l'équation :
En d'autres termes, le vecteur quantité de mouvement p décrit un cercle de rayon mk/L centré en (0, A/L). L'excentricité e correspond au cosinus de l'angle η vu à la Figure 3. Il est également intéressant d'introduire la variable
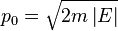
Obtention de l'orbite de Kepler
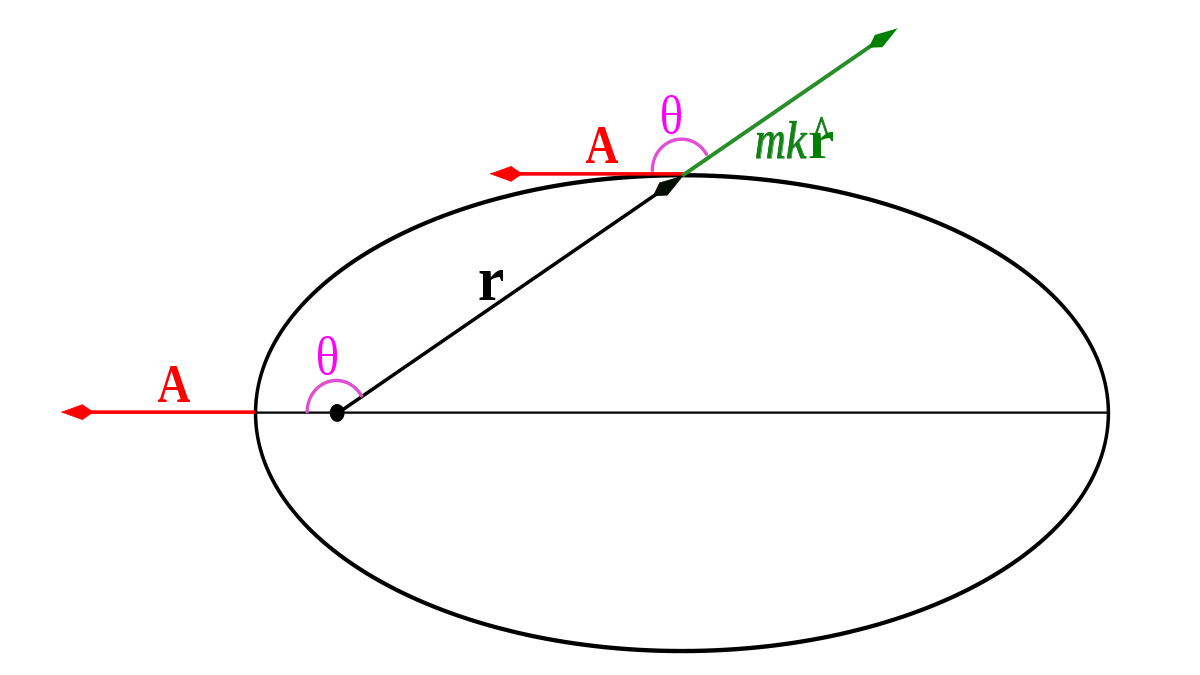
La forme et l'orientation des orbites dans le problème à deux corps de Kepler peuvent être déterminées à partir du vecteur de Runge-Lenz comme suit. Le produit scalaire de A par le vecteur position r donne l'équation
où θ est l'angle entre r et A (Figure 2). En permutant le produit mixte
et un réarrangement conduit à la formule de définition d'une conique
d'excentricité

et de paramètre p
Le demi grand-axe a de la conique peut être obtenu à partir du paramètre et l'excentricité
où le signe moins désigne une ellipse et le signe plus une hyperbole.
La norme de A mène à une équation faisant intervenir l'énergie E
ce qui peut être réécrit en termes d'excentricité
Donc, si l'énergie est négative (état lié) l'excentricité est inférieure à un et l'orbite est une ellipse. Si l'énergie est positive (état libre ou état de diffusion), l'excentricité est supérieure à un est l'orbite est une hyperbole. Pour finir, si l'énergie est exactement égale à zéro l'orbite est une parabole (excentricité égale à 1). Dans tous les cas A est colinéaire à l'axe de symétrie de la conique et est dirigé du centre de force vers le periapside, point de plus courte approche.
Évolution dans des potentiels perturbés

Le vecteur de Runge-Lenz A est conservé uniquement pour une force centrale suivant loi strictement en carré inverse. Dans la plupart des problèmes pratiques tels que les mouvement de planètes, l'énergie potentielle d'interaction entre deux corps ne découle pas rigoureusement d'une telle loi et peut inclure un terme additif, appelé potentiel de perturbation h(r). Dans de tels cas le vecteur de Runge-Lenz tourne lentement dans le plan de l'orbite ce qui correspond à une lente précession du périastre de l'orbite. Par hypothèse le potentiel de perturbation h(r) est conservatif et central, ce qui implique que l'énergie totale E et le vecteur moment cinétique L sont conservés. En conséquence le mouvement reste contenu dans un plan perpendiculaire à L et la norme de A se conserve selon l'équation A2 = m2k2+2mEL2. Le potentiel de perturbation h(r) peut être n'importe quelle fonction mais doit être significativement plus petit que le potentiel découlant de la force en carré inverse entre les deux corps.
La vitesse à laquelle le vecteur de Runge-Lenz tourne donne des informations sur le potentiel de perturbation h(r). En utilisant la théorie des perturbations canoniques et les coordonnées action-angle, on obtient immédiatement que A tourne à la vitesse
où T est la période orbitale et dans laquelle l'identité L dt = m r2 dθ a été utilisée pour convertir l'intégrale temporelle en intégrale angulaire (Figure 5). L'expression entre crochets, 〈h(r)〉, représente la moyenne sur une période du potentiel de perturbation, c'est-à-dire la moyenne pour la particule décrivant complètement une fois son orbite. Mathématiquement la moyenne temporelle, qui est la grandeur entre accolades, permet d'éliminer les fluctuations dans le taux de rotation.
Cette approche a été utilisée pour permettre une vérification de la théorie d'Einstein de la relativité générale, qui ajoute un terme cubique de perturbation au potentiel gravitationnel newtonien
En injectant cette fonction dans l'intégrale et en utilisant l'équation
pour exprimer r en fonction de θ, la précession du périastre due à des perturbations non-newtonniennes est
ce qui correspond étroitement à l'anomalie observée de la précession de Mercure et des pulsars binaires. Cet accord avec l'expérience est considéré comme une preuve importante de la validité de la relativité générale.
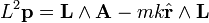
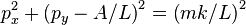
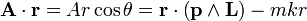
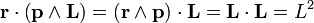
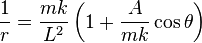
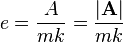
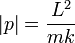
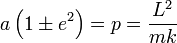
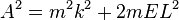
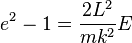
![\begin{array}{rcl} \frac{\partial}{\partial L} \langle h(r) \rangle & = &\displaystyle \frac{\partial}{\partial L} \left\{ \frac{1}{T} \int_{0}^{T} h(r) \, dt \right\} \\[1em] & = & \displaystyle\frac{\partial}{\partial L} \left\{ \frac{m}{L^{2}} \int_{0}^{2\pi} r^{2} h(r) \, d\theta \right\}. \end{array}](https://static.techno-science.net/illustration/Definitions/autres/7/7a77441627c8cfd5e7664e58d9287458_55f0584cb1c9b1b70207847e6fc56df0.png)