Variété (géométrie) - Définition

Approfondissements

Structures connexes

Pour mettre en œuvre la géométrie sur des variétés, il est souvent requis d'ajouter des structures additionnelles à ces espaces, tels que ceux vus plus haut pour les variétés différentielles. Il existe de nombreuses autres possibilités, dépendant du type de géométrie qu'on cherche à introduire :

• Variété analytique : la définition est analogue à celle de variété différentielle, mais on impose que les applications de changement de cartes soient des difféomorphismes analytiques. Toute variété différentiable admet une structure de variété analytique.

• Variété complexe : une variété holomorphe est une variété construite sur Cⁿ à l'aide de fonctions de transitions holomorphes sur des recouvrements de cartes. Ces variétés sont les objets de base pour l'étude de la géométrie complexe. Une variété à une dimension complexe est appelée surface de Riemann. (Noter qu'une variété complexe à n dimensions a 2 n dimensions en tant que variété différentielle réelle.)

• Variété de Banach ou variété banachique et Variété de Fréchet : pour permettre l'extension aux dimensions infinies, on peut considérer des variétés de Banach qui soient localement homéomorphes à des espaces de Banach. De même, les variétés de Fréchet sont localement homéomorphes à des espaces de Fréchet.

• Variété à singularités coniques : incluent les variétés différentielles, les variétés différentielles à bord, les cônes, les polyèdres, aussi bien en tant que surfaces qu'en tant que solides.

• Orbifold : Un orbifold est la généralisation des variétés pour certains types de singularité dans la topologie.

• Variété algébrique et schéma : une variété algébrique est construite par assemblage de variétés algébriques affines, qui sont des ensembles de zéros de polynômes construits sur des corps. La domestication des recollements à opérer n'est plus basée sur la régularité des changements de cartes, mais en décrivant lesquelles des fonctions définies localement sur la variété méritent d'être considérées comme régulières ; la notion de faisceau se substitue alors à celle d'atlas comme outil technique pour la définition. Les schémas sont de même construits à partir de schémas affines, qui sont eux-mêmes une généralisation des variétés algébriques affines.

• CW-complexe : un CW-complexe est un espace topologique formé d'objets de différentes dimensions par recollements successifs. Pour cette raison, ce n'est généralement pas une variété. Cependant, il est d'un intérêt central en topologie algébrique : il permet de coder la topologie et d'en donner une approche essentiellement combinatoire. Toute variété topologique admet une décomposition en CW-complexe.

Classification des variétés

Un problème central en mathématiques concerne la possibilité d'identifier deux objets ensemblistement distincts mais dont les propriétés sont semblables. En ce sens, deux variétés sont identifiées lorsqu'il existe une bijection entre elles qui soit compatible avec la topologie. Une telle bijection est appelée homéomorphisme. Par exemple, le cercle considéré comme sous-variété du plan, ou le cercle abstrait construit par recollement, s'ils sont ensemblistement différents, sont homéomorphes. Du point de vue de la topologie, la surface d'un ballon de foot ou d'un ballon de rugby est la même. Les différences entre ces deux objets sont de nature métrique.

Le problème général devient : quand peut-on identifier deux variétés topologiques à homéomorphisme près ? Deux variétés différentielles à difféomorphisme près ?

Les premiers résultats dans ce sens, très partiels, concernent la classification des surfaces, aujourd'hui bien connue. Cette classification repose sur la caractéristique d'Euler, et le genre. Cette caractéristique se généralise aisément aux dimensions supérieures, grâce à la notion de faces de dimension supérieure. Ce qui importe est alors la configuration des triangulations des variétés, et la caractéristique d'Euler ne code qu'une partie des informations sur ces triangulations. Pour avoir accès aux informations restantes, il faut abandonner l'idée d'invariants numériques, et étudier des invariants algébriques associés aux triangulations : c'est la naissance des méthodes homologiques et cohomologiques, suivant les idées de Poincaré sur l'homologie singulière. Des méthodes homotopiques, dont le niveau élémentaire est l'étude de la simple connexité, apportent aussi des réponses.

Ces méthodes s'adaptent, dans un certain sens, en considérant d'autres cohomologies, aux types de variété plus rigides : par exemple, la cohomologie de De Rham pour l'étude des variétés différentielles. Les invariants obtenus ne forment en général pas des systèmes complets d'invariants : c'est-à-dire que deux variétés peuvent topologiquement se distinguer, alors qu'elles sont cohomologiquement semblables, au sens où leurs groupes de cohomologie sont identiques.

Nœud de trèfle dans l'espace de dimension trois.

Un autre problème intéressant de classification provient des déformations des sous-variétés plongées : on ne s'autorise alors plus n'importe quelle déformation, mais seulement certaines qui respectent la topologie de l'espace sous-jacent, les homotopies, ou bien les isotopies, suivant le problème considéré. À nouveau, des méthodes cohomologiques et homotopiques sont utiles. On obtient des classifications plus fines, où le nœud trèfle, et le cercle, confondues homéomorphiquement, sont cette fois bien distincts. La théorie des nœuds notamment s'intéresse au plongement d'un cercle dans l'espace à trois dimensions, ou dans la sphère tridimensionnelle.

Toujours plus en avant, la théorie des nœuds a permis de donner la construction effective des variétés de dimension 3. En quelques mots, toute variété compacte de dimension 3 s'obtient en effectuant un nombre fini d'opérations sur la sphère tridimensionnelle au voisinage d'un nombre fini de nœuds disjoints. Pour chaque nœud, il s'agit d'en retirer un voisinage, un tore plein, et de le recoller différemment. La topologie de la variété ne dépend que de la classe d'homotopie des données de recollement, qui sont des homéomorphismes du tore. L'argumentation est détaillée dans l'article Variété différentielle de dimension 3, ou l'ouvrage de Dale Rolfsen. L'utilisation d'un unique nœud trivial donne naissance à un ensemble de variétés compactes de dimension 3, appelées espaces lenticulaires.

Discussions autour des variétés

Lors d'études plus approfondies sur la topologie des variétés sont rencontrées des discussions récurrentes portant sur la dimension des variétés ou la rigidité des structures :

• Les petites dimensions offrent peu de degrés de liberté. De fait, il n'est pas rare que des structures pourtant différentes en grandes dimensions coïncident en dimensions 1, 2, 3, éventuellement 4, 5. Cependant, l'excès de contraintes peut rendre l'approche difficile. À cet égard, citons le problème posé par Poincaré concernant la caractérisation topologique d'une sphère de dimension n. La preuve en dimension 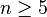a valu la médaille Fields à Stephen Smale en 1966, la preuve en dimension 4 a valu la médaille Fields à Michael Freedman en 1986, la preuve en dimension 3 a valu la médaille Fields à Grigori Perelman en 2006 (mais celui-ci l'a refusée).
• La seconde thématique concerne la souplesse ou la rigidité des structures additionnelles sur les variétés.