Variété (géométrie) - Définition

Un exemple détaillé : le cercle

Les quatre cartes du premier atlas.

Après la droite réelle, l'exemple le plus simple de variété est le cercle. Il existe essentiellement deux manières de l'introduire : on pense ici à un cercle tracé dans le plan euclidien R², dont les coordonnées usuelles sont notées x et y. Par une similitude, on se ramène à un cercle de centre (0,0) et de rayon 1. Un tel cercle est implicitement défini par l'équation x² + y² = 1.

Un premier atlas

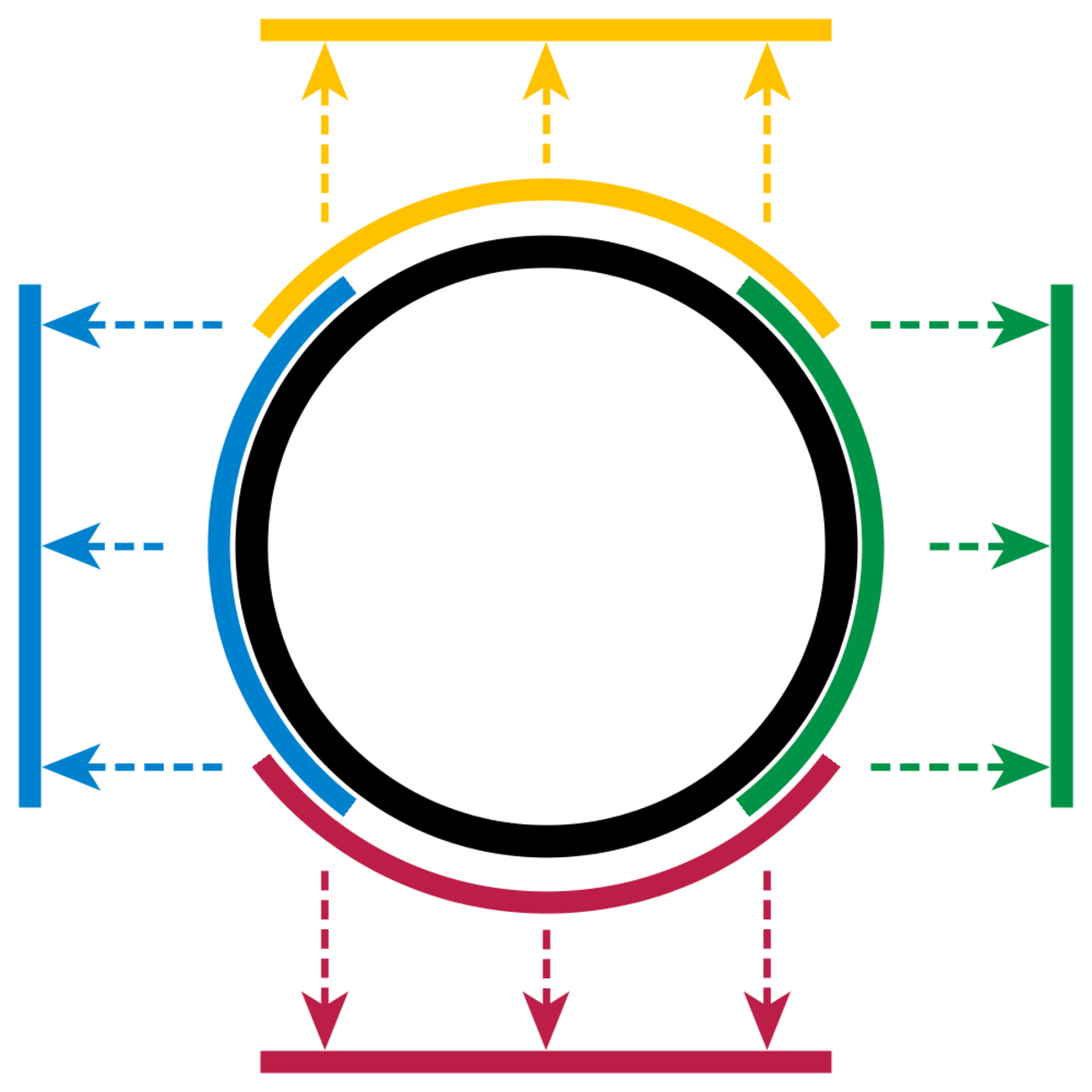
Localement, le cercle ressemble à une ligne, qui est à une dimension. En d'autres termes, une seule coordonnée suffit pour décrire un petit arc de cercle. Considérons par exemple la partie supérieure du cercle, pour laquelle la coordonnée y est positive (partie jaune sur la Figure 1). N'importe quel point de cette partie peut être décrit par la coordonnée x. Il y a donc un homéomorphisme χ_haut, qui relie la partie jaune du cercle à l'intervalle ouvert ]−1, 1[ en représentant chaque point du cercle par sa première coordonnée :

Une telle fonction est appelée une carte. De manière similaire, il existe des cartes pour les parties inférieure (rouge), gauche (bleue) et droite (verte) du cercle. Ensembles, elles recouvrent la totalité du cercle et on dit que les quatre cartes forment un atlas de ce cercle.

Les deux cartes supérieure et gauche se recouvrent. Leur intersection est située dans le quart de cercle où les coordonnées x et y sont respectivement négative et positive. La carte χ_haut réalise une bijection qui à (x,y) associe x, partant de la zone de recouvrement vers l'intervalle ]-1,0[. La carte χ_gauche par laquelle (x,y) donne y associe à cette même zone de recouvrement l'intervalle ]0;1[. Ainsi, il est possible de créer une fonction T de l'intervalle ]-1,0[ vers ]0,1[ :

Une telle fonction est appelée une application de changement de carte ou de transition. Elle permet de passer du système de coordonnées x choisi pour la première carte au système de coordonnées y choisi pour la seconde.

Un autre atlas

L'application pente forme une carte décrivant tous les points du cercle sauf un.

Les cartes supérieure, inférieure, gauche et droite montrent que le cercle est une variété, mais ne constituent pas le seul atlas envisageable. Les cartes n'ont pas besoin d'être des projections géométriques, et le nombre de cartes est presque arbitraire.

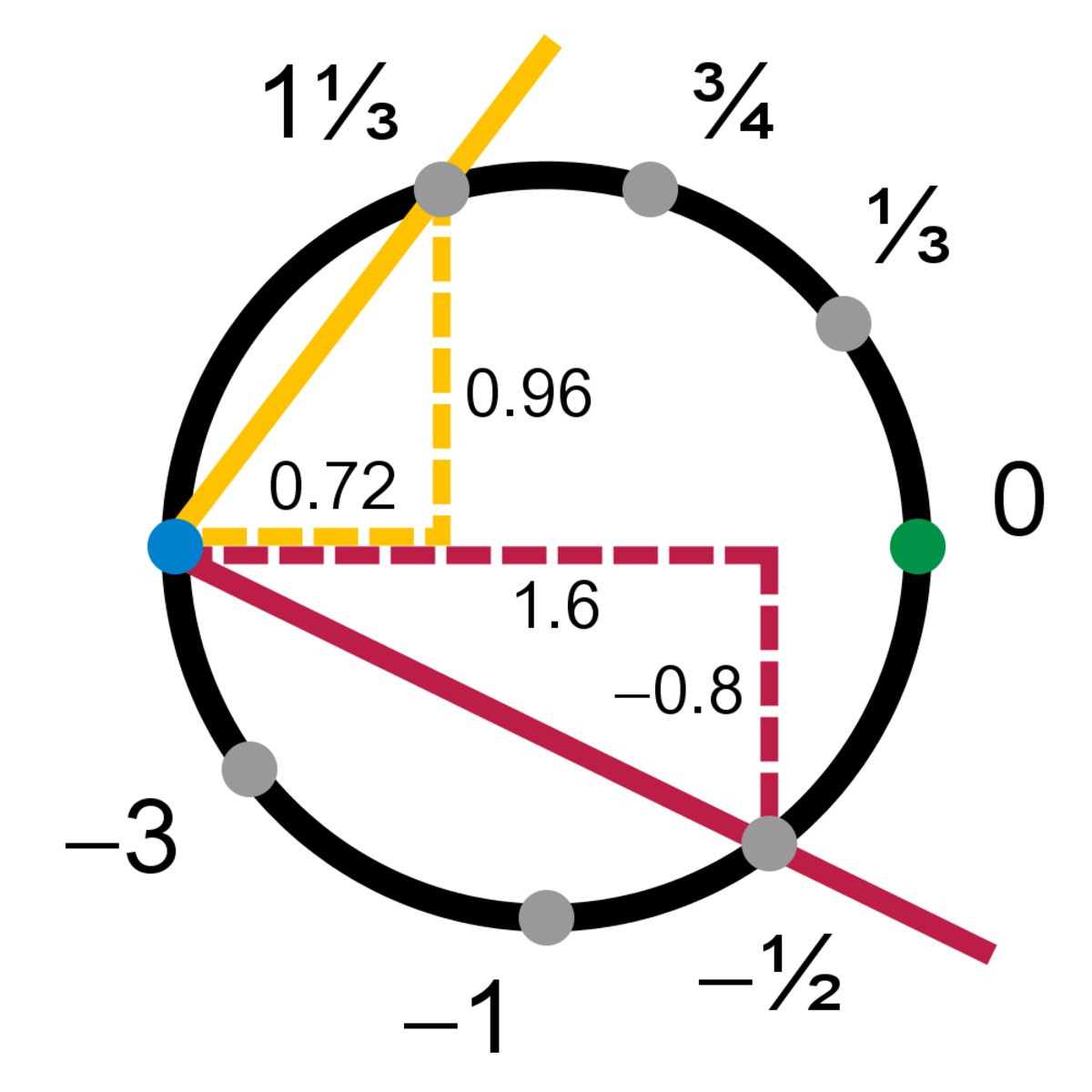
Voici un autre exemple de description du cercle. Prenons pour point de base le point de coordonnées (-1, 0) et traçons les différentes droites issues de ce point ; la droite de pente s recoupe le cercle en un point unique. La correspondance entre la pente de la droite et les coordonnées du point d'intersection est dans un sens :

 ;

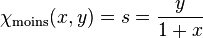et dans l'autre sens :

.

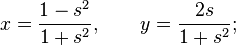Cette première carte décrit tous les points du cercle hors le point de base.

Pour fabriquer la deuxième carte on effectue une symétrie en prenant comme point de base (+1, 0) et comme pente -t avec :

.

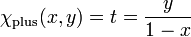Ces deux cartes fournissent un second atlas du cercle, avec pour application de changement de carte

.

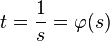Noter que chaque carte omet un point unique, soit (−1,0) pour s ou (+1,0) pour t, donc aucune des cartes seule ne peut décrire complètement le cercle.

Bilan

On vérifierait que les deux atlas présentés sont compatibles, c'est-à-dire qu'en regroupant les quatre cartes du premier et les deux cartes du second, on obtient un nouvel atlas, encore plus redondant. Chacun des deux atlas, ainsi que l'atlas global, définissent donc la même notion de repérage par carte et coordonnées locales, c'est-à-dire la même structure de variété. On montrerait encore, à l'aide du théorème des fonctions implicites que la donnée de l'équation x² + y² = 1 permet aussi de créer des systèmes de cartes locales adaptées.

On voit donc à travers ces exemples la flexibilité amenée par l'utilisation de cartes : on dispose d'un choix infini d'atlas compatibles sur le cercle, qu'il faut prendre adaptés à la géométrie du problème étudié. Cependant, à l'aide d'arguments topologiques on peut montrer qu'une carte seule ne peut jamais couvrir l'ensemble du cercle.

En dimension supérieure

Cette carte associe la partie rouge de la sphère à un disque.

Carte tracée par projection stéréographique, représentant toute la sphère sauf son pôle nord.

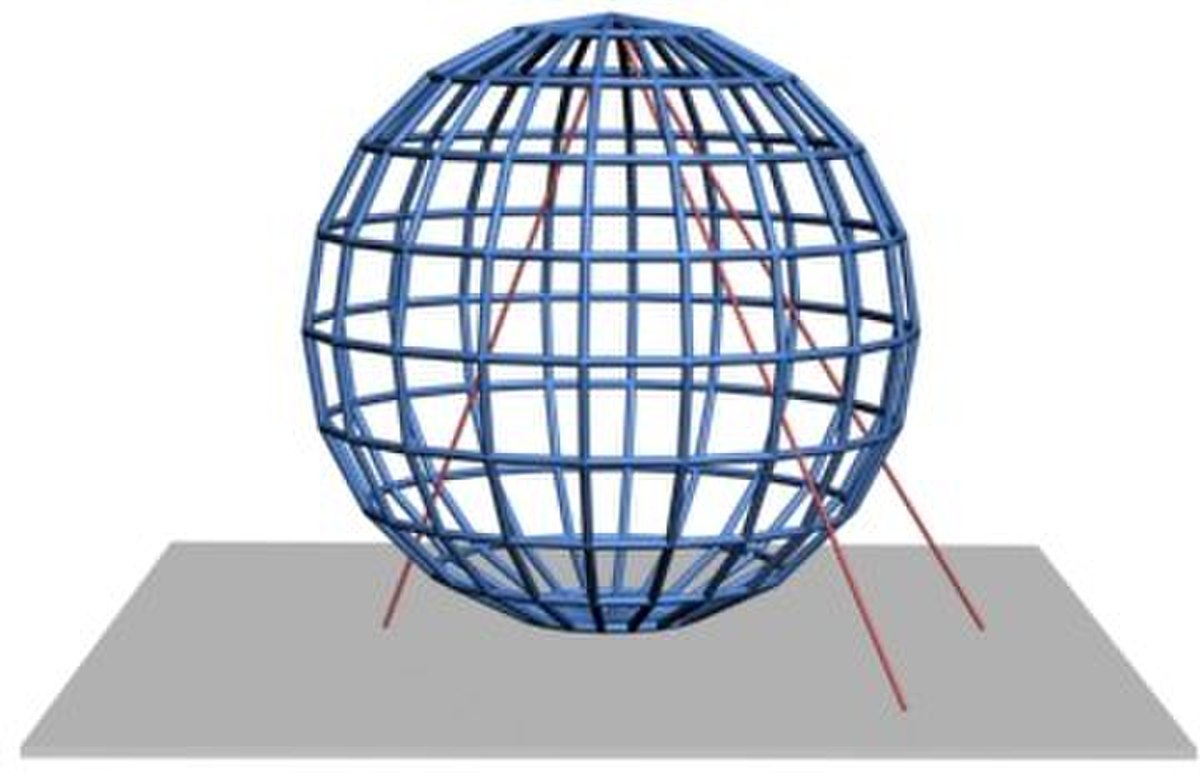
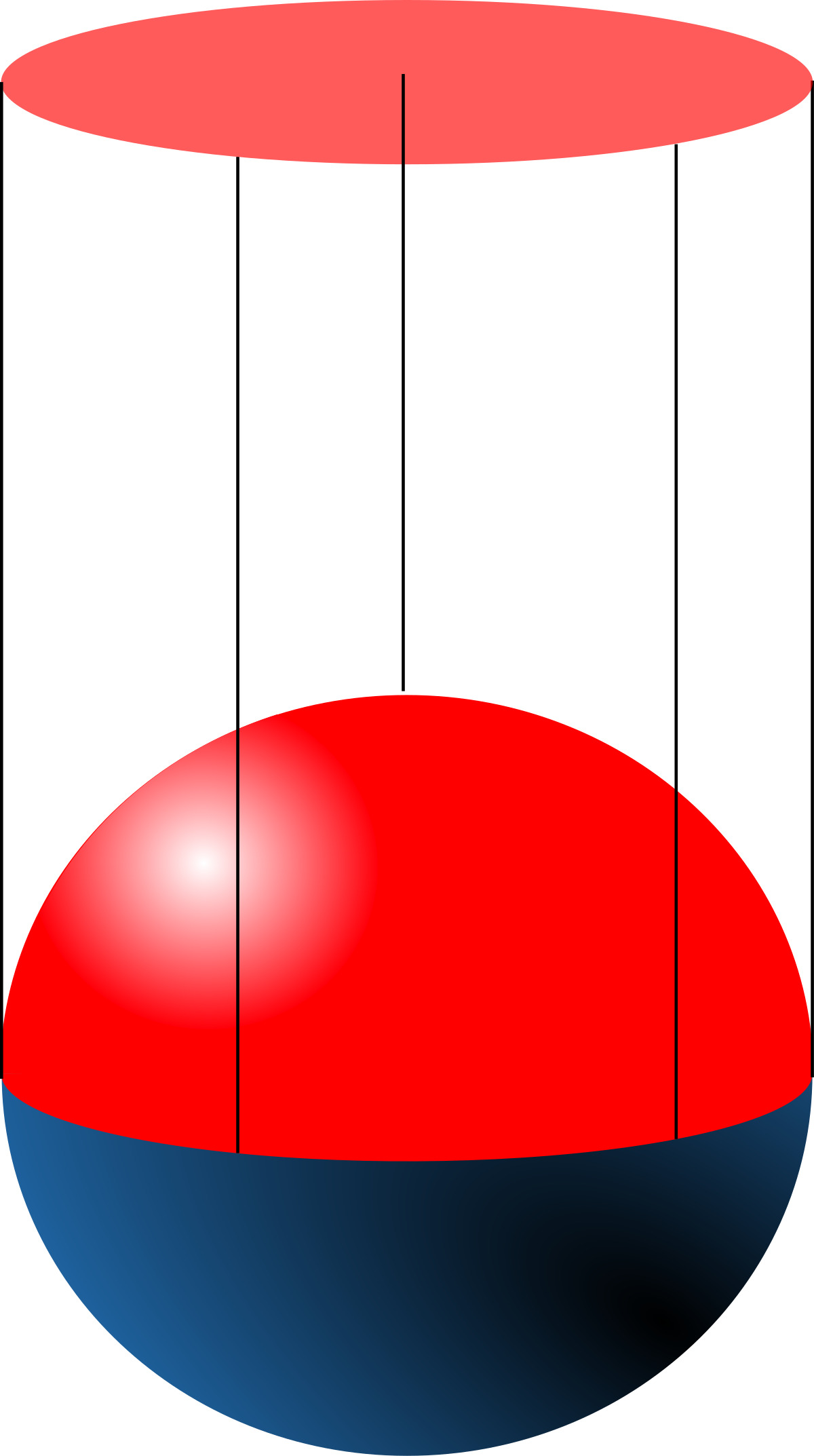
La méthode envisagée pour le premier atlas du cercle peut aisément être généralisée pour des sphères de dimension supérieure. La n-sphère Sⁿ est une généralisation de l'idée de cercle (1-sphère) et de sphère (2-sphère) à des dimensions supérieures. Une n-sphère Sⁿ peut être construite en considérant 2(n+1) cartes correspondant aux deux projections sur chacun des n+1 hyperplans de coordonnées, et les applications de changement de cartes. Une carte pour un tel atlas est illustré ci-contre dans le cas de la 2-sphère.

Dans le cas de la 2-sphère, c'est-à-dire du globe usuel, le deuxième atlas envisagé pour le cercle admet aussi une généralisation : c'est un atlas constitué des deux projections stéréographiques depuis les pôles nord et sud respectivement.