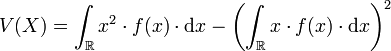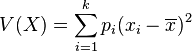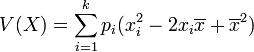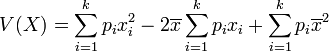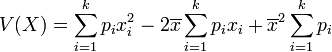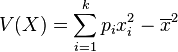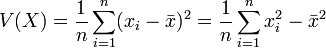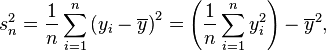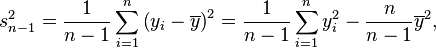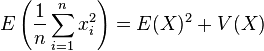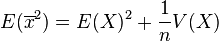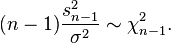Variance (statistiques et probabilités) - Définition
La liste des auteurs de cet article est disponible ici.
Cas continu
Dans le cas continu, la variance se calcule de la façon suivante :
Cas discret
La variance V(X) représente la moyenne des carrés des écarts à la moyenne : elle permet de caractériser, tout comme l'écart type, la dispersion des valeurs xi par rapport à la moyenne, notée
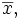
Soit une série statistique
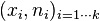
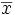
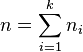
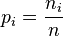
La variance de cette série est alors :
Simplification
La moyenne peut être considérée comme le barycentre de la série.
D'après le théorème de König , on a :
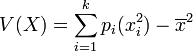
Or,
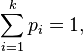
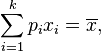
Équiprobabilité
Dans le cas d'équiprobabilité,
Remarque: égalité toujours vraie, même s'il n'y a pas équiprobabilité! (cf développer le calcul et sortir la moyenne de la somme dans le terme croisé)
Estimation
Deux estimateurs sont généralement utilisés pour la variance:
et
Propriétés
Biais
- L'estimateur
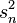
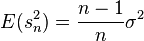
L'estimateur
-
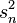
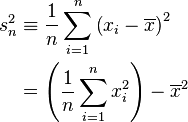
La deuxième égalité s'obtient d'après le théorème de König-Huyghens.
Nous allons calculer l'espérance de l'estimateur d'après la deuxième formule:
-
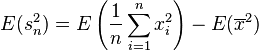
Il faut donc étudier l'espérance des deux termes, on verra que:
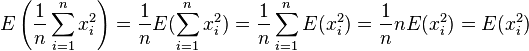
On a supposé que tous les réalisations ont la même espérance: E(xi) = E(X) En appliquant de nouveau la formule de König-Huyghens:
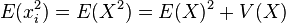
Etudions au préalable l'espérance et la variance de la moyenne:
- La moyenne
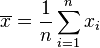
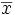
- -d'espérance
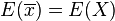
- -de variance:
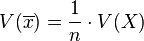
- -d'espérance
En appliquant de nouveau la formule de König-Huyghens:
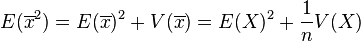
On a donc
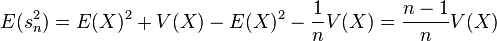
- La variance s de l'échantillon fluctue donc autour de
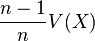
- L'estimateur
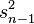
Démonstration — En effet, il suffit de corriger l'estimateur
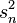
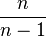
![E\left[\frac{n}{n-1} s^2_{n}\right]= \frac{n}{n-1} E[s^2_{n}]=\frac{n}{n-1} \frac{n-1}{n}\sigma^2=\sigma^2](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/8e50ebdefd648d0d1d0b4e10c15b9788_a93ca24fa0638f1a1195b623f7a3253d.png)
Pourquoi n-1?
Le fait que l'estimateur de la variance doive être divisé par n-1 (et donc dans un certain sens moins précis) pour être sans biais provient du fait que l'estimation de la variance implique l'estimation d'un paramètre en plus, l'espérance. Cette correction tient compte donc du fait que l'estimation de l'espérance induit une incertitude de plus. En effet:
Théorème — si l'on suppose que l'espérance est connue, l'estimateur
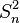
en reprenant la démonstration du biais de
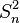
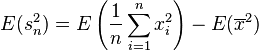
Cependant, le deuxième calcul est désormais différent: E[X] étant connu, on pose que E[X] = μ et on a: E[μ2] = E[μ]2
Donc on a directement:
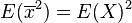
La formule devient alors:
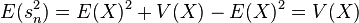
Convergence
Les estimateurs
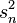
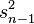
Théorème —
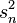
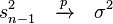
Réecrivons l'estimateur:
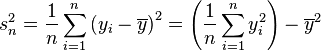
Et étudions la convergence des termes séparément:
-
-
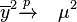
![\frac 1n \sum_{i=1}^n \left(y_i - \overline{y} \right)^ 2 \xrightarrow{p} \quad \operatorname{E}[x^2]= \mu^2+\sigma^2](https://static.techno-science.net/illustration/Definitions/autres/3/3839c2631c6fc359cd668ee9dd0ddabb_de5f73b4314140cdaacd966b00748fa6.png)
![\frac 1n \sum_{i=1}^n \left(y_i - \overline{y} \right)^ 2 \xrightarrow{p} \quad \operatorname{E}[x^2]= \mu^2+\sigma^2](https://static.techno-science.net/illustrationWebp/Definitions/autres/3/3839c2631c6fc359cd668ee9dd0ddabb_de5f73b4314140cdaacd966b00748fa6.png)
Alors
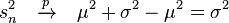
Comme ce résultat est asymptotique, il s'applique également à
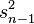
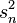
Distribution des estimateurs
En tant que fonction de variables aléatoires, l'estimateur de la variance est également une variable aléatoire. Sous l'hypothèse que les yi sont des observations indépendantes d'une loi normale, le théorème de Cochran (en) montre que
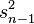
En conséquence, il suit que
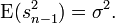
Méthodes de calcul
Le calcul par ordinateur de la variance empirique peut poser certains problèmes, notamment à cause de la somme des carrés. La page anglaise: Algorithms for calculating variance décrit le problème ainsi que des algorithmes proposés.
