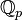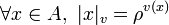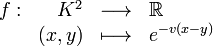Valuation - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Propriétés générales
Soit A un anneau commutatif unitaire non nul muni d'une valuation v. Alors :
- v(1) = v( − 1) = 0 ;
-
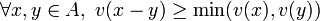
-
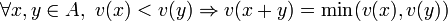
- A est intègre ;
- il existe une unique valuation w sur le corps des fractions Frac(A) qui prolonge A :
-
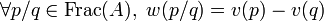
Valuations discrètes sur le corps des rationnels
Les places de


- la valuation triviale ;
- les valuations p-adiques (cf. exemple ci-dessous).
Valeur absolue associée
Soit v une valuation sur A à valeur dans
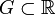
![\rho \in ]0,1[](https://static.techno-science.net/illustration/Definitions/autres/2/29eb2711bb839c25779875bc5ee7e41a_d375f5c457fbc005bafef1b338b6a5d6.png)
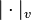
Anneau de valuation
Soit K un corps commutatif muni d'une valuation v. Les éléments de K de valuation positive ou nulle constituent un sous-anneau R appelé l' anneau de valuation associé à la valuation v sur K :
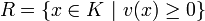
Le corps des fractions de R est K.
On a v(1/x) = - v(x) pour tout élément non nul x de K, et donc x est un élément inversible de R si et seulement si v(x) = 0. Par conséquent, R est un anneau local dont l'unique idéal maximal M est constitué des éléments de valuation strictement positive :
 .
.Par exemple (pour les valuations usuelles sur ces corps) l'anneau de valuation de
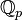
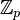
Il existe diverses caractérisations des anneaux de valuation:
Soient R un anneau commutatif unitaire intègre et K son corps des fractions. Les conditions suivantes sont équivalentes :
- R est un anneau de valuation (pour une certaine valuation sur K)
- pour tout élément x de K qui n'appartient pas à R, l'inverse de x appartient à R,
- sur l'ensemble des idéaux principaux de R, l'ordre défini par l'inclusion est total,
- sur l'ensemble des idéaux de R, l'ordre défini par l'inclusion est total.
Deux valuations v et v' sur K sont dites équivalentes si elles ont le même anneau de valuation. Ceci équivaut à l'existence d'un isomorphisme de groupes ordonnés
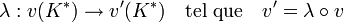
Le point de vue métrique
Si v une valuation sur un corps K, alors l'application
est une distance sur K qui fait de K un corps topologique. La topologie sur K associée à cette distance est la plus petite rendant v continue pour la topologie de l'ordre sur G. On dit que K est complet pour v s'il est complet pour cette distance.
La complétion de K pour v est le procédé décrit ci-dessous :
- On note A l'anneau des suites de Cauchy de F, et on identifie les éléments de A aux suites constantes. La valuation de K se prolonge à A en une valuation encore notée v. L'ensemble I des suites de Cauchy tendant vers 0 est un idéal maximal de A sur lequel la valuation est triviale.
- Le quotient de A par I est un corps commutatif C, que l'on appelle complété de K pour v, et K s'identifie canoniquement à un sous-corps de C. On obtient sur C une valuation qui prolonge v. Le corps K est dense dans C, pour cette valuation sur C.
Par exemple,