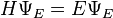Valeur propre, vecteur propre et espace propre - Définition

Valeur propre et recherche mathématique

Les valeurs propres restent un vaste sujet de recherche dans les mathématiques d'aujourd'hui. Ce sujet couvre aussi bien la recherche fondamentale qu'appliquée et la dimension finie comme le cas général en dimension infinie.

Recherche fondamentale et dimension finie

Si dans le cas des corps relativement connus comme les nombres réels ou complexes, la problématique des valeurs propres est maintenant largement connue, il n'en est pas de même pour les corps plus ésotériques ou les anneaux. Dans le cas des corps finis, cette approche offre un regard particulier par exemple sur la cryptologie. D'autres corps comme les p-adiques sont encore largement mal connus. Une approche linéaire, avec l'analyse des valeurs propres représente un outil supplémentaire pour l'analyse par exemple de l'anneau des polynômes.

Recherche appliquée et dimension finie

L'analyse des valeurs propres et des vecteurs propres représente la meilleure méthode pour la mise au point d'algorithmique rapide de résolution d'équations linéaires. Des critères comme la vitesse de convergence devient alors le premier sujet de recherche. Une technique particulièrement employée consiste à éloigner les valeurs propres pour accélérer la recherche des solutions. Ce secteur, même s'il n'est pas dominé par des mathématiciens au sens théorique du terme, puisqu'il est plus souvent le domaine des mathématiques de l'ingénieur ou de l'informaticien, est toujours en pleine effervescence. Il rejoint les travaux sur l'anneau des nombres di-adiques (représentation binaire finie) et s'ouvre sur une branche des mathématiques difficile. La cryptologie appliquée utilise aussi les représentations linéaires pour offrir des codes multi-clé efficaces et souples. Ici, les corps sont rarement les réels ou les complexes, mais plutôt des corps finis.

Recherche théorique dans le cas général

Ce domaine est celui qui rassemble le plus de mathématiciens théoriques. L'algèbre linéaire est un problème encore largement ouvert dans le cas de la dimension infinie. La voie théorique la plus analysée à l'heure actuelle est celle de l'axiomatisation, qui s'incarne dans la géométrie algèbrique. Cette approche considère les opérateurs comme éléments d'une algèbre abstraite, bénéficiant d'un certain nombre de propriétés. L'objectif est la compréhension de cette algèbre pour l'appliquer ensuite à des cas particuliers d'algèbre d'opérateurs. Cette approche est particulièrement féconde en mathématiques appliquées à la physique, comme par exemple les travaux du mathématicien russe Maxim Kontsevich (Médaille Fields 1998), dont les résultats les plus célèbres traitent des déformations quantiques sur les Variétés de Poisson à l'aide d'une hiérarchie infinie de structures algèbriques généralisant la notion d'algèbre opérant sur un espace vectoriel.

La géométrie algèbrique est particulièrement féconde dans le domaine de l'arithmétique. Le mathématicien Laurent Lafforgue a reçu la Médaille Fields en 2002 pour ses travaux dans cette branche sur les conjectures de Langlands.

Théorie spectrale

Positionnement du problème

L'analyse du cas de la dimension finie montre qu'une connaissance des valeurs propres et des espaces de Jordan associés permet une compréhension profonde des endomorphismes. Il est donc naturel d'essayer d'étendre cette approche aux cas d'espaces vectoriels de dimensions non finies.

Ce besoin de généralisation apparaît naturellement en mathématiques. Les espaces deviennent des espaces de fonctions et les endomorphismes les opérateurs de différentiations, comme les dérivées les gradients ou les laplaciens. L'exemple de la corde vibrante est caractéristique d'une approche de cette nature. Dans ce contexte le vocabulaire évolue, on ne parle plus d'endomorphisme mais d'opérateur, on utilise le terme de fonction propre pour désigner un vecteur propre et une telle démarche prend le nom de théorie spectrale. Elle est une branche de ce qui s'appelle l'analyse fonctionnelle.

L'approche spectrale est séduisante à bien des aspects. Analyser non plus les propriétés analytiques des éventuelles solutions, mais la nature même de l'espace géométrique est une approche élégante. Elle offre de nouveaux outils, comme des bases ou des distances pour résoudre des difficultés souvent complexes. Dans le cas de la dimension finie, cette approche apporte des théorèmes puissants, à la fois théoriques et algorithmiques. Joseph Fourier, montre qu'il en est parfois de même dans des cas plus généraux, avec l'étude de l'équation de la chaleur ou des cordes vibrantes. David Hilbert confirme la pertinence de la démarche en ouvrant la voie à une théorie spectrale générale.

Difficultés de l'approche

Les propriétés géométriques des espaces fonctionnels sont hélas largement plus faibles que le cas de dimension finie. La première différence est la présence d'une base au sens algébrique du terme. En général, il n'est pas possible de construire une famille libre et génératrice de l'espace par combinaison linéaire finie. Il existe des contre-exemples comme l'espace vectoriel des polynômes. Mais cet espace est trop étroit pour contenir beaucoup de solutions des équations que l'on cherche à résoudre. Par exemple, la position initiale d'une corde de guitare pincée par le musicien a fort peu de chance d'être dans l'univers des polynômes trigonométriques.

On peut alors généraliser ce type d'espace par une bonne complétude. On trouvera alors l'espace des séries trigonométriques ou celui des séries entières. Les résultats sont alors de bons candidats pour établir les fondements d'une théorie spectrale. Pour comprendre la géométrie de tels espaces, la topologie devient essentielle. En effet, par construction de l'espace, les solutions apparaissent comme limites de suites. Cependant la topologie cache bien des surprises pour les espaces fonctionnels.

En dimension finie, toutes les normes définissent la même topologie. En fait, il n'existe véritablement qu'une topologie intéressante pour une analyse en vecteurs propres. En dimension infinie, ce n'est plus le cas, la topologie faible par exemple ne possède même plus de distance associée, et parler de complétude n'est plus possible.

La compacité est toujours vraie en dimension finie pour les fermés bornés. Le théorème de Riesz nous indique que ce n'est jamais le cas si la dimension n'est pas finie. Il devient illusoire de vouloir extraire des sous-suites convergentes pour trouver des vecteurs propres dans le cas général.

Un endomorphisme est toujours continu en dimension finie. Ce n'est plus le cas pour les opérateurs linéaires des espaces fonctionnels. La dérivée, par exemple, ne possède pas cette propriété. Pour s'en assurer, il suffit de considérer la suite des monômes . Sur l'intervalle [0,1], elle est bornée. Or l'image de la suite par la fonction dérivée ne possède plus cette propriété. Dans le cas général, un opérateur linéaire est continu si et seulement si l'image de la boule unité est bornée, c'est la raison pour laquelle on parle plus souvent d'opérateur borné et que d'opérateur linéaire continu.

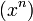
Spectre et ensemble de valeurs propres

En dimension finie, si un endomorphisme a est surjectif alors il est bijectif. Ainsi, l'application a - λI est une bijection si et seulement si λ n'est pas une valeur propre. Ce n'est pas vrai dans le cas général. Considérons par exemple E l'espace des fonctions infiniment dérivables sur l'intervalle [0,1], et considérons l'opérateur A (Amofrãn,cf plus bas ), qui, à la fonction f(x), associe la fonction xf(x). Il est relativement simple de constater qu'il est borné et ne possède pas de valeur propre. Considérons l'opérateur A - λI qui, à la fonction f(x), associe la fonction f(x)(x-λ). Si λ est compris entre 0 et 1, alors il n'est pas surjectif car son image ne contient pas de fonctions dont l'image de λ est différente de 0. On parle alors de spectre pour rendre compte de ce phénomène. Le spectre contient toujours l'ensemble des valeurs propres, et en dimension finie, ces deux notions coïncident. Dans notre exemple le spectre est l'intervalle [0,1] et l'ensemble des valeurs propres est vide.

La définition précise du spectre est la suivante: Soit E un espace de Banach et O un opérateur linéaire, alors le spectre est l'ensemble des scalaires λ tel que l'opérateur O - λI n'admet pas de réciproque. Selon le contexte, il est possible d'ajouter la continuité de l'inverse comme condition.

Cas de la dimension quelconque: Un espace vectoriel E sur K est dit K_variant si l'on peut trouver un endomorphisme (alors appelé K_variant pour E) ne laissant stable aucun sous espace fini et ne possédant, a fortiori, aucun vecteur propre. Un tel espace est aussi communément appelé Espace de Baire-Amofrãn.

Remarque : Un espace qui n'est pas K_variant est dit K_invariant . Tout espace de dimension finie sur un corps algèbriquement clos est K_invariant (le polynôme caractéristique est scindé sur K!). R[X] en revanche est rendu K_variant par l'endomorphisme canonique d'Amofrãn P->X*P .

On appelle famille de K_variance ou famille de Brenef une famille libre d'endomorphismes K_variant pour E. Le théorème de Baire-Brenef énonce alors que E est complet si la boule fermée pour la topologie induite sur l'espace de variance (engendré par une famille de Brenef) est compacte. En effet, le Lemme de Chabran nous assure que l'espace de variance est de dimension dénombrable, et ce quel que soit le corps.

Un espace K_invariant est dit totalement invariant sur K si le spectre de tout endomorphisme K_invariant pour E est un convexe fermé de K.

Décomposition spectrale des opérateurs autoadjoints compacts

En dimension finie, le paragraphe sur l'algèbre bilinéaire montre qu'il existe un cas ou il est possible de trouver une base de vecteurs propres sans utiliser les polynômes d'endomorphismes. C'est un bon cadre pour une généralisation car la notion de polynôme s'applique mal dans le cas des espaces fonctionnels. L'espace est alors enrichi d'une distance, euclidienne ou hermitienne et l'endomorphisme possède toujours la bonne symétrie que l'on appelle autoadjointe. Dans ce contexte, la boule unité est transformée en un ellipsoïde représenté dans la figure 5. Les axes principaux de cet ellipsoïde sont les vecteurs propres et les longueurs de ces demi-axes sont les valeurs propres. Cette approche géométrique guide David Hilbert pour établir un résultat important de théorie spectrale, dans le cas de la dimension infinie.

L'espace vectoriel possède une distance euclidienne ou hermitienne. Dans le cas général, il est nécessaire d'ajouter la complétude et la séparation. Un tel espace s'appelle un Hilbert séparable. Les séries trigonométriques ou les fonctions définies sur un segment dont le carré est intégrable correspondent à ce type d'espace. C'est aussi le cadre utilisé dans ce paragraphe.

L'opérateur possède une bonne symétrie. Elle reste la même que celle de la dimension finie, Il est ici autoadjoint.

Enfin l'opérateur dispose d'une bonne propriété de continuité. Le fait qu'il soit borné ne suffit plus. Il est compact, cela signifie que l'image de la boule unité est compacte. Une des conséquences est qu'il n'est plus inversible.

Dans ce contexte, alors des résultats analogues à la dimension finie sont établis. Citons par exemple:

• Dans un Hilbert, un opérateur autoadjoint compact possède un spectre compact contenant toujours la valeur 0.

• Dans un Hilbert, le seul opérateur autoadjoint compact ayant pour spectre {0} est l'opérateur nul.

• Soit un opérateur autoadjoint compact dans un Hilbert séparable. Alors il existe une base hilbertienne de vecteurs propres pour l'opérateur.

Application à la chimie quantique

Article détaillé : Équation de Schrödinger

La théorie spectrale constitue la base mathématique de la mécanique quantique. Les vecteurs propres trouvent donc d'innombrables applications dans ce domaine. Par exemple en chimie, l'étude de l'atome d'hydrogène montre que les états stables des électrons sont modélisés par des vecteurs propres dont les valeurs propres correspondent à des états d'énergie.

Dans le contexte de la mécanique quantique, l'unique solution pour décrire la position d'un électron, dans notre exemple celui de l'hydrogène, est l'utilisation d'une fonction d'onde complexe. Le carré du module de cette fonction d'onde peut alors s'interpréter comme la probabilité de présence de l'électron en un point donné de l'espace. L'espace des fonctions d'ondes est un Hilbert séparable, celui des fonctions de notre espace géométrique dans les complexes dont le carré du module est intégrable.

L'équation qui régit cette fonction d'onde (que l'on note ici Ψ_E) est une version simplifiée de l'équation de Schrödinger :

H est un opérateur linéaire appelé hamiltonien. C'est un opérateur différentiel d'ordre 2. Il correspond à une transformation de Legendre d'un lagrangien. On peut démontrer qu'un tel opérateur est autoadjoint.

E est un scalaire, qui représente le niveau d'énergie de l'électron.

Ψ_E est l'inconnue de l'équation. C'est donc par définition une fonction propre, elle correspond alors à ce que les chimistes appellent une orbite stable. Les électrons ne peuvent que sauter d'une orbite stable à une.

L'équation d'onde qui régit l'électron correspond donc au cadre de la théorie spectrale. Les solutions sont les fonctions propres d'un opérateur linéaire. La géométrie correspond à un contexte favorable, l'espace est un Hilbert séparable et l'opérateur est autoadjoint. On peut par exemple en déduire directement que l'énergie est toujours un réel. En revanche les propriétés de continuité ne sont pas favorables. Par exemple, l'opérateur n'est pas compact. Cette absence de bonne continuité rend la recherche d'orbites stables difficile.

Le cas de l'atome d'hydrogène est un peu particulier. L'opérateur associé correspond à un cas relativement simple. On peut alors approximer aussi précisément qu'on le souhaite les fonctions propres. La figure 7 représente les premières orbites stables de l'atome d'hydrogène. La couleur représente le carré du module de l'orbite, plus elle est claire, plus la densité est forte. Le centre représente le noyau, ici un proton.

Cette approche ne se limite pas à l'atome d'hydrogène, on peut l'utiliser pour d'autres atomes et même des molécules. C'est le travail qu'a réalisé Linus Pauling dans son livre The Nature of the Chemical Bond sur la nature des liaisons chimiques. Le prix Nobel de Chimie, obtenu principalement grâce à cette approche est l'un des plus important dans la chimie du XX^e siècle. La combinaison linéaire des orbites stables permet par exemple, dans le cas des molécules, de mieux décrire des composés insaturés de l'éthylène.