Valeur propre, vecteur propre et espace propre - Définition
La liste des auteurs de cet article est disponible ici.
Définition
Définition intuitive
Une application linéaire est une application qui transforme les vecteurs en conservant les propriétés d'addition des vecteurs et les rapports de colinéarité entre vecteurs. Ainsi, si un vecteur w est la somme de deux vecteurs u et v, alors l'image de w par l'application est la somme de l'image de u et de l'image de v. De plus l'image par exemple de 3v est 3 fois l'image de v. Plusieurs transformations géométriques usuelles (homothétie de centre 0, rotation de centre 0) sont des applications linéaires.
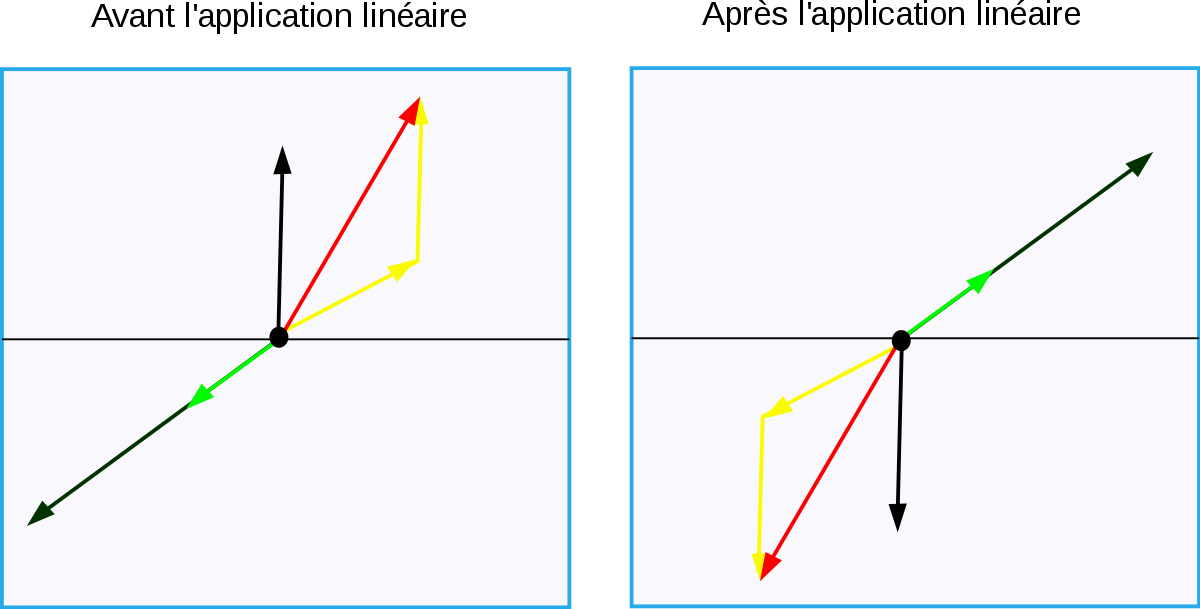
La figure 2 illustre par un exemple une application linéaire. On remarque que le vecteur rouge est la somme des deux vecteurs jaunes avant transformation, et que c'est encore le cas après. De même le vecteur noir est le triple du vecteur vert avant la transformation, et ça reste le cas une fois qu'on l'a appliquée. On voit un vecteur propre en gris de valeur propre -1 : on passe du vecteur initial au vecteur image par multiplication de rapport -1.
- Un vecteur est dit vecteur propre par une application linéaire s'il est non nul et si l'application ne fait que modifier sa taille sans changer sa direction (à ne pas confondre avec son sens !).
- Une valeur propre associée à un vecteur propre est le facteur de modification de taille, c’est-à-dire le nombre par lequel il faut multiplier le vecteur pour obtenir son image. Ce facteur peut être négatif (renversement du sens du vecteur) ou nul (vecteur transformé en un vecteur de longueur nulle).
- Un espace propre associé à une valeur propre est l'ensemble des vecteurs propres qui ont une même valeur propre et le vecteur nul. Ils subissent tous la multiplication par le même facteur.
Définition mathématique
Soit E un espace vectoriel sur
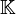
- Le vecteur x de E non nul est dit vecteur propre de u si et seulement s'il existe un élément λ de
- le scalaire λ élément de
- soit λ une valeur propre de u alors l'ensemble constitué des vecteurs propres de valeur propre λ, et du vecteur nul, forme un sous-espace vectoriel de E appelé espace propre de u associé à la valeur propre λ.
Le vocabulaire des éléments propres dans différentes disciplines
- En mécanique, on étudie les fréquences propres et les modes propres des systèmes oscillants.
- En analyse fonctionnelle, une fonction propre est un vecteur propre pour un opérateur linéaire, c'est-à-dire une application linéaire agissant sur un espace de fonctions.
- En géométrie ou en optique, on parle de directions propres pour rendre compte de la courbure des surfaces.
- En théorie des graphes, une valeur propre est simplement une valeur propre de la matrice d'adjacence du graphe.
Théorie en dimension finie
Approche élémentaire
Article détaillé : Polynôme caractéristique
Une première remarque simplifie l'étude. Si λ est une valeur propre d'un endomorphisme u, alors un vecteur propre est un vecteur non nul qui a pour image 0 par l'application u - λ.Id, où Id désigne l'application identité. L'espace propre associé à λ est l'ensemble des vecteurs qui ont pour image 0 par cette application. On appelle cet ensemble le noyau de l'endomorphisme u - λ.Id. Les propriétés générales établissent que cet ensemble est un sous espace vectoriel. Celui-ci est non réduit à 0 par définition d'une valeur propre.
Une fonction importante, en particulier dans notre cadre, est la fonction déterminant. Elle fut la première à être étudiée systématiquement dans le monde de l'algèbre linéaire. Elle associe à un endomorphisme un nombre. Son intérêt réside notamment dans le fait que le déterminant d'un endomorphisme est nul si et seulement s'il existe des vecteurs non nuls qui ont pour image le vecteur nul par cet endomorphisme, c'est-à-dire si et seulement si 0 est une valeur propre pour cet endomorphisme. Le déterminant de l'application u - λ.Id est appelé le polynôme caractéristique. Ces remarques fournissent les premières propriétés :
-
- Soit λ une valeur propre, alors l'espace propre de valeur propre λ est le sous-espace vectoriel égal au noyau de u - λ.Id,
- un espace propre est un sous-espace vectoriel,
- les racines du polynôme caractéristique sont les valeurs propres.
Cette dernière propriété montre que l'existence de racines de polynômes a une influence sur la théorie des valeurs propres. En fait, l'existence même des valeurs propres dépend de l'existence de racines pour les polynômes, par exemple le polynôme caractéristique. C'est pourquoi dans le cadre du corps des nombres complexes, qui est algébriquement clos d'après le théorème de d'Alembert-Gauss, les propriétés liées aux valeurs propres s'énonceront plus simplement que dans le cadre du corps des réels.
-
- Les espaces propres Ei de valeurs propres λi forment une somme directe de sous-espaces vectoriels stables par u.
Cette propriété se démontre simplement avec les outils développés dans l'article Polynôme d'endomorphisme. X - λi est un polynôme annulateur de la restriction de u à Ei. Ces polynômes sont tous premiers entre eux, la dernière proposition du paragraphe Idéaux annulateurs termine la démonstration.
-
- Toute famille de p vecteurs propres de u associés à des valeurs propres deux à deux distinctes est une famille libre.
Cette propriété est un corollaire direct de la proposition précédente.
-
- Si deux endomorphismes u et v commutent, alors un espace propre de u est stable par v.
Soit x un vecteur propre de u, de valeur propre λ, alors:
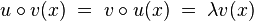
Nous avons donc démontré que v(x) est soit nul soit vecteur propre de valeur propre λ il est donc bien élément de l'espace propre de x.
Cas où l'endomorphisme est diagonalisable
Article théorique: Diagonalisation, article appliqué: Matrice diagonalisable
Le concept de l'article est particulièrement clair dans le cas où le comportement de l'endomorphisme est entièrement décrit par les vecteurs et valeurs propres. L'endomorphisme est alors dit diagonalisable.
- Un endomorphisme est dit diagonalisable si et seulement s'il existe une base de vecteurs propres.
C'est le cas du premier exemple, celui du miroir. Une base peut alors être choisie en prenant deux vecteurs libres dans le plan de la glace et un troisième perpendiculaire à ce plan. Les deux premiers vecteurs ont pour images eux-mêmes et sont donc de valeur propre 1 et le dernier est de valeur propre -1. Cette situation est intéressante à trois titres: elle correspond à un cas simple à traiter, elle est sous certaines hypothèses fréquente, enfin il existe de multiples critères pour la repérer.
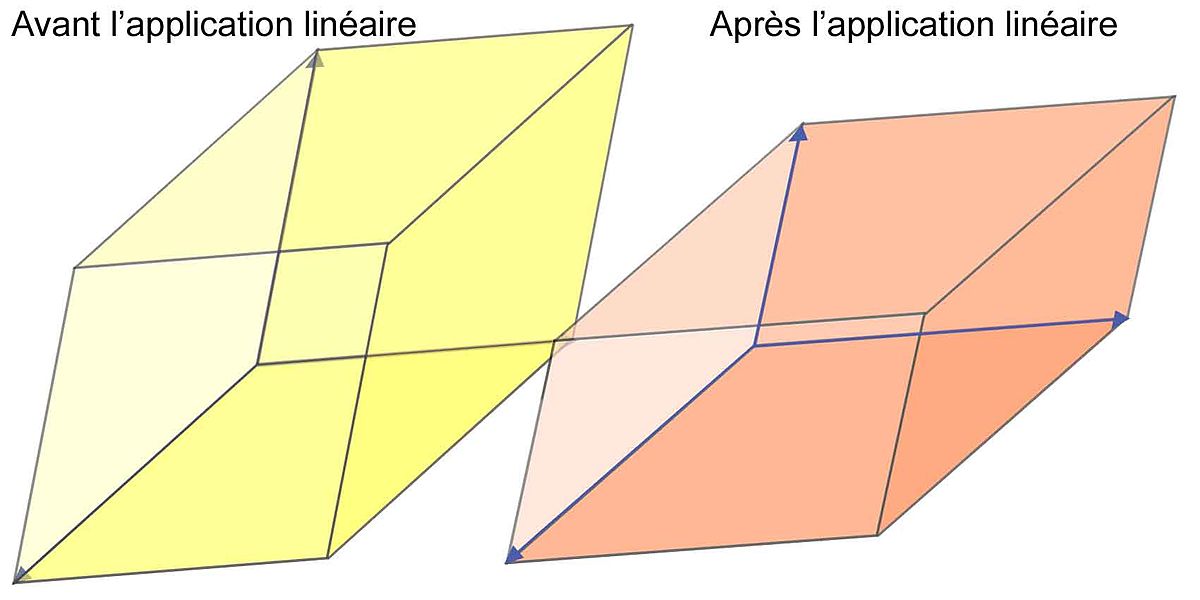
- La simplicité de cette situation provient de deux faits. Il existe une décomposition de l'espace en sous-espaces stables, simples en eux-mêmes, et sur lesquels l'endomorphisme est simple à décrire. Ces sous-espaces sont simples car de dimension 1 : ce sont des droites. La linéarité de l'endomorphisme permet de connaître exhaustivement le comportement de la transformation, une fois compris le comportement sur ces droites. Enfin la restriction de l'endomorphisme à ces droites est une homothétie, c’est-à-dire une dilatation, d'un facteur la valeur propre. Un exemple de cette situation est donné par la figure 10 : un parallélotope jaune dont les arêtes sont la base de vecteurs propres, l'image par l'endomorphisme est un parallélotope dont les arêtes ont gardé les mêmes directions, mais dont les longueurs ont été modifiées.
Cette simplicité ouvre la voie à de nombreuses applications évoquées précédemment dans l'article. Elle permet par exemple le calcul d'une exponentielle d'endomorphisme et par conséquent la résolution de nombreux problèmes mécaniques.
- Cette situation est aussi fréquente. La figure 11 en est une illustration dans le cas où l'espace vectoriel est de dimension 2 sur les nombres réels. L'ensemble des endomorphismes est alors un espace de dimension 4 : tout endomorphisme admet une représentation matricielle de la forme
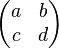
- Enfin il existe de multiple critères pour caractériser un endomorphisme diagonalisable. Une première approche consiste à étudier le polynôme caractéristique. Une autre largement plus sophistiquée consiste à étudier les polynômes de l'endomorphisme. L'un des concept clé est alors le polynôme minimal qui fournit, par exemple, un critère de diagonalisation particulièrement simple.
Les critères associés à la diagonalisation sont données dans la boite déroulante suivante. Les articles contenant les preuves sont systématiquements cités.
Les propositions suivantes sont équivalentes:
-
- L'endomorphisme est diagonalisable
- Il existe une base de vecteur propre
- la somme des espaces propres engendre l'espace entier
- la somme des dimensions des espaces propres est égale à la dimension de l'espace entier
- toute représentation matricielle de u est diagonalisable.
Dans le cas complexe (c’est-à-dire ou le corps de nombre est celui des complexes) cette propriété est presque partout vraie au sens de la mesure. Au sens de la topologie les endomorphismes diagonalisables sont denses.
Démonstration dans Diagonalisation.
-
- Les racines du polynôme minimal forment l'ensemble des valeurs propres.
Démonstration dans Valeur propre (synthèse)
-
- Un endomorphisme u est diagonalisable si et seulement son polynôme minimal est scindé sur K et à racines simples.
Démonstration dans Polynome d'endomorphisme
-
- S'il existe n valeurs propres distinctes alors l'endomorphisme est diagonalisable.
Démonstration dans Valeur propre (synthèse)
-
- Si l'endomorphisme est diagonalisable, alors le polynôme caractéristique est scindé.
Démonstration dans Réduction d'endomorphisme
L' ordre de multiplicité algébrique d'une valeur propre est l'ordre de multiplicité de la racine dans le polynôme caractéristique. L'ordre de multiplicité algébrique d'une valeur propre λ correspond donc à la puissance du monôme (X-λ) dans le polynôme caractéristique. L'adjonction de cette définition permet l'expression d'une condition nécessaire et suffisante de diagonalisabilité.
-
- L'endomorphisme est diagonalisable si et seulement si, tout espace propre possède une dimension égale à la multiplicité algèbrique de la valeur propre associée.
Démonstration dans Réduction d'endomorphisme
Les démonstrations associées à la nappe de l'adhérence des endomorphismes non diagonalisables sont données dans Diagonalisation.
Cas Complexe
Article détaillé : Réduction de Jordan
La figure 11 montre que, même dans le cas où le corps est celui des nombres complexes, il reste encore des cas à élucider, celui des endomorphismes qui se situent sur la nappe, mais pas sur la droite des homothéties. Dans le cas des systèmes d'équations différentiels linéaires, il n'intervient que comme un cas limite, dans l'approche de Sylvester, il n'apparaît plus du tout. En revanche dans la théorie des groupes, ce cas est important. Ce type d'endomorphisme permet la représentation des groupes non commutatifs. Si ces groupes sont infiniement différentiable, alors ils permettent la représentation d'un cas important, celui des groupes de Lie nilpotent.
Pour élucider cette problématique, les méthodes utilisées sont celles mises au point par Nelson Dunford. L'outil essentiel consiste à considérer les combinaisons linéaires de puissance de l'endomorphisme. On obtient ainsi un polynôme d'endomorphisme. Ces polynômes forment une structure d'algèbre commutative doté d'un morphismes de l'ensemble des polynômes vers cette algèbre. Cette approche est féconde, on la retrouve aussi dans l'étude du cas où la dimension n'est plus finie. La théorie associée à cette approche se trouve dans l'article Polynôme d'endomorphisme, et l'application au cas traité ici dans Décomposition de Dunford.
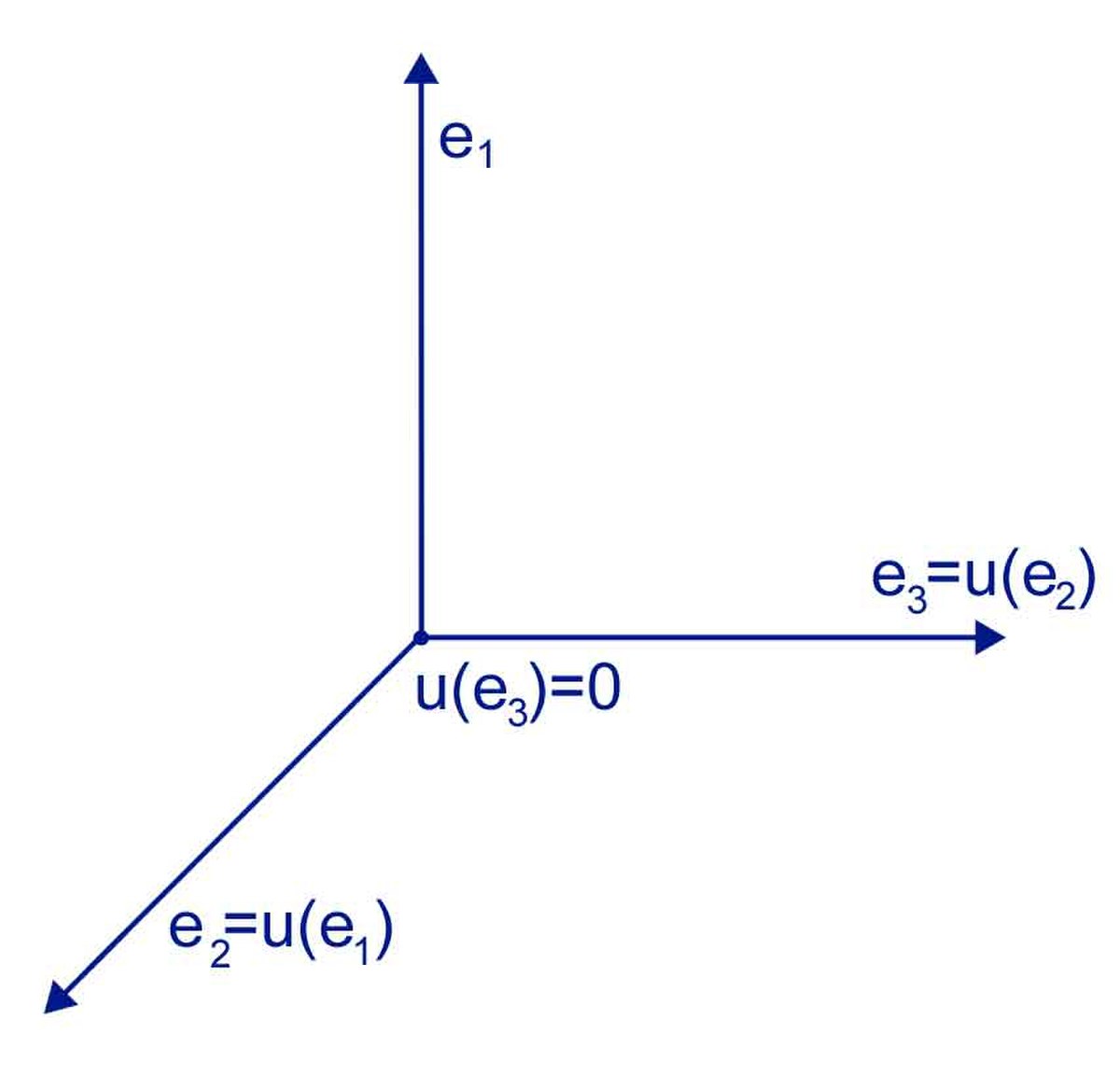
Le résultat remarquable est qu'il n'existe dans ce contexte qu'une unique exception structurelle au cas diagonalisable. C'est le cas où l'endomorphisme u à la puissance p, où p est un entier, est égal à 0. On dit alors que l'endomorphisme est nilpotent. On peut considérer par exemple en dimension 3, si (e1, e2, e3, ) est une base l'endomorphisme qui vérifie u(e1)=e2, u(e2)=e3 et u(e3)=0. Cet endomorphisme n'est clairement pas nul son polynôme caractéristique est égal à x3 donc la seule valeur propre est 0. Cet exemple est illustré en figure 12.
Camille Jordan a prouvé que dans ce contexte, tout endomorphisme est somme d'un endomorphisme diagonalisable et d'un endomorphisme nilpotent et qu'ils commutent entre eux. L'application de la théorie des endomorphismes montre que le cas nilpotent dispose d'une représentation matricielle particulièrement simple et trigonale supérieure. Dans le cas général, cette représentation s'appelle la réduction de Jordan, elle démontre aussi que, dans ce cas, toute matrice est semblable à une matrice triangulaire.
-
- L'endomorphisme u est la somme d'un endomorphisme diagonalisable et d'un endomorphisme nilpotent qui commutent entre eux.
Démonstration dans Polynôme d'endomorphisme
-
- L'espace E est somme directe de ses espaces caractéristiques.
Démonstration dans Décomposition de Dunford
La notion de espace caractéristique généralise l'espace propre. Elle correspond au noyau de l'endomorphisme (u - λ.Id)n.
-
- Les sous-espaces caractéristiques sont non réduits au vecteur nul et stables par l'endomorphisme. La restriction de l'endomorphisme à l'espace propre associé à la valeur propre λ est la somme d'une homothétie de rapport λ et d'un endomorphisme nilpotent.
Démonstration dans Décomposition de Dunford
-
- Un espace propre est inclus dans l'espace caractéristique de même valeur propre.
Démonstration dans Décomposition de Dunford
-
- La famille de projecteurs sur les espaces caractéristiques ainsi que les endomorphismes diagonalisables et nilpotents s'expriment sous forme de polynômes d'endomorphisme de u.
Démonstration dans Décomposition de Dunford
-
- Toute matrice de u est trigonalisable, il admet une représentation de Jordan.
Démonstration dans Réduction de Jordan
-
- Le polynôme minimal est le produit des polynômes de degré 1 et de racine les valeurs propres à la puissance l'indice de l'endomorphisme nilpotent associé.
Démonstration dans Décomposition de Dunford
-
- Le polynôme caractéristique est le produit des polynômes de degré 1 et de racine les valeurs propres à la puissance la dimension de l'espace caractéristique associé.
Démonstration dans Décomposition de Dunford
-
- Le déterminant est égal au produit des valeurs propres élevées à la puissance de la dimension de l'espace caractéristique associé.
Démonstration dans Décomposition de Dunford
-
- La trace est égale à la somme des valeurs propres multipliées par la dimension de l'espace caractéristique associé.
Démonstration dans Décomposition de Dunford
Cas Réel

Sur les réels un polynôme n'admet pas toujours de racine. Dans notre troisième exemple, celui de la rotation de la terre, l'espace est de dimension 3, or tout polynôme du troisième degré possède une racine sur les réels. En conséquence, il existe au moins une droite de vecteurs propres. C'est l'axe des pôles dans notre exemple. En revanche, dans le cas de dimension paire, par exemple la restriction de cette application au plan illustré en bleu sur la figure 13 de l'équateur, l'existence de valeur propre n'est plus garantie. Ici, une analyse géométrique nous montre qu'il est vain de chercher un vecteur propre car la rotation modifie la direction de tous les vecteurs non nuls.
Dans le cas complexe, nous avons vu que seul un terme nilpotent peut interdire la diagonalisation. Dans le cas réel, une fois retranché le terme nilpotent, seul les rotations empêchent la diagonaliation. Il existe alors deux manières de réduire le cas réel.
La première solution consiste à plonger l'endomorphisme dans un espace vectoriel complexe. C'est la solution la plus simple et la plus fréquente. La réduction de l'endomorphisme y est alors plus aisée. Une fois cette réduction réalisée, l'application de cette réduction à des vecteurs réels donnent toujours des solutions réelles.
La deuxième solution consiste à affaiblir la réduction. Tout endomorphisme sur les nombres réels est la somme du produit d'un endomorphisme diagonalisable et d'une rotation avec un endomorphisme nilpotent. L'endomorphisme diagonalisable commute avec l'application nilpotente et la rotation. En revanche, l'application nilpotente ne commute pas avec la rotation.
Démonstration dans Réduction d'endomorphisme
Cas d'un module sur un anneau
Les définitions n'utilisent pas le fait que
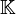
Cas des formes bilinéaires
Article associé: Théorème spectral
Les endomorphismes sont aussi utilisés pour représenter des formes bilinéaires, qui sont des objets de même nature que les distances euclidiennes. Les valeurs et vecteurs propres prennent dans ce contexte une signification particulière.
Les formes bilinéaires sont des fonctions qui ne sont pas linéaires, mais quadratiques, au sens où la fonction ne s'exprime plus comme une combinaison linéaire de coordonnées, c'est-à-dire un polynôme (à plusieurs variables) de degré 1 en les coordonnées, mais comme un polynôme du second degré en les coordonnées. La distance euclidienne sur l'espace
Certaines propriétés éventuellement vérifiées par les formes bilinéaires, comme par exemple la symétrie, les rendent le cas échéant plus faciles à étudier. La distance euclidienne par exemple est symétrique, ainsi la distance d'un point a à un point b est la même que la distance d'un point b à un point a. Un endomorphisme qui représente une forme bilinéaire symétrique est dit autoadjoint.
Ces endomorphismes autoadjoints disposent en fait de propriétés fortes concernant valeurs et vecteurs propres: non seulement ils admettent des vecteurs propres, mais de plus ceux-ci suffisent pour comprendre entièrement l'endomorphisme ; un endomorphisme auto-adjoint est diagonalisable. Ensuite, les vecteurs propres peuvent être choisis avec une propriété forte : il existe une base orthonormale de vecteurs propres. Enfin, pour ce cas particulier, il existe des méthodes de calcul simples et rapides pour obtenir valeurs et vecteurs propres. Cette situation est illustrée graphiquement sur la figure 5. Un endomorphisme autoadjoint transforme la boule unité en un ellipsoïde dont les axes sont les vecteurs propres et les longueurs des demi-axes les valeurs absolues des valeurs propres.
Par ailleurs, la forme bilinéaire initiale décrit ici l'équivalent d'une distance d'un espace géométrique ; l'espace étudié, muni de la forme bilinéaire, est un nouvel espace géométrique. Sylvester montre que les vecteurs et valeurs propres, de l'endomorphisme auto-adjoint associé, sont des invariants, des êtres qui décrivent les grandeurs naturelles et caractéristiques de la géométrie considérée. La signification physique de ces grandeurs dépend du contexte de l'espace étudié. Sylvester a appliqué ce qui précède au principe d'inertie d'un solide indéformable en mécanique et en avait déduit l'existence d'axes de rotation (vecteurs propres) et de constantes d'inertie (valeurs propres) intrinsèques au solide. Les autres exemples d'applications montre qu'il en est de même dans d'autres situations, par exemple en statistique où les composantes principales révèlent la dimension la plus significative d'un songage, ou la relativité qui montre l'existence d'un invariant, la signature de Sylvester, dans la structure même de la géométrie de notre univers.
Le rôle des vecteurs et valeurs propres est ainsi modifié. Ils ne sont plus des uniquement des outils de calculs nécessaires pour accélérer un algorithme ou pour résoudre un problème technique de résolution d'équation différentielle, ils acquièrent une autonomie propre, et deviennent des invariants constitutifs d'une géométrie. Ils prennent alors des noms spécifiques au domaine d'application ; on parle par exemple d'axe de rotation en mécanique, de composantes principales en statistiques, ou de directions propres dans le cas d'espaces courbes.
La démonstration de l'existence d'une base de vecteurs propres dans le cas des endomorphismes autoadjoints est donnée dans l'article Endomorphisme autoadjoint.