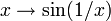Valeur d'adhérence - Définition
La liste des auteurs de cet article est disponible ici.
Cas général
La notion de valeur d'adhérence d'une suite dans un espace topologique généralise celle de valeur d'adhérence d'une suite réelle sous sa formulation , laquelle signifiait, dit informellement, que chaque intervalle ]a-ε,a+ε[ contient "une infinité de termes" de la suite.
Définitions
Soient E un espace topologique,
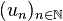
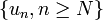
Il suffit pour cela qu'il existe une sous-suite de (un) qui converge vers a. Cette dernière condition est équivalente à la définition si tout point de E admet une base dénombrable de voisinages. C'est le cas par exemple si E est un espace métrique.
Plus généralement, si f est une fonction d'un espace topologique E dans un espace topologique F, on dit que y est une valeur d'adhérence de f en un point x de E si y est adhérent aux images par f de tous les voisinages de x.
Exemples
- Considérons l'ensemble E égal à la réunion de
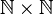
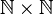
-
- il existe N tel que, pour tout n supérieur ou égal à N, U contienne tous les points de
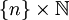
- il existe N tel que, pour tout n supérieur ou égal à N, U contienne tous les points de
- Considérons la suite parcourant
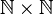
-
- Cette suite admet ω comme valeur d'adhérence, mais aucune sous-suite ne converge vers ω.
- Les valeurs d'adhérence au point 0 de la fonction numérique