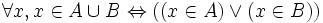Union (mathématiques) - Définition

Définition

L'union des ensembles A et B

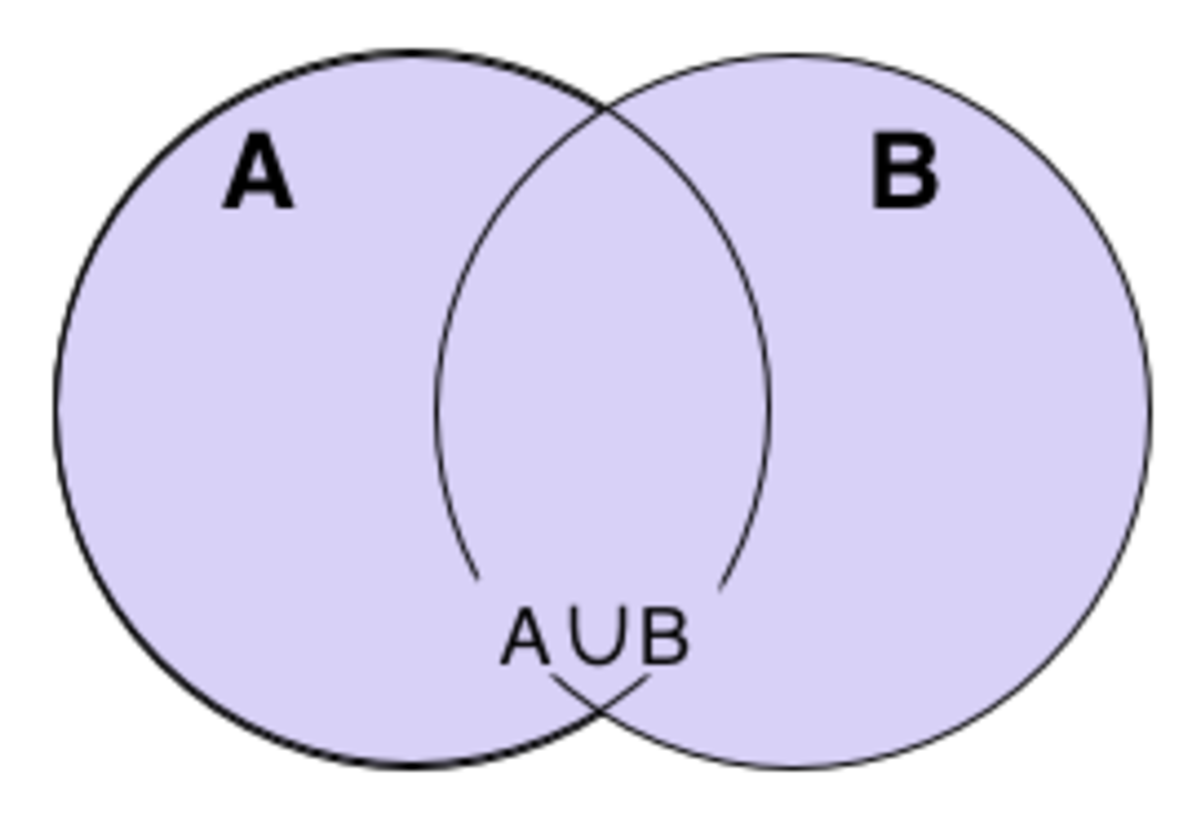
Dans la théorie des ensembles, l'union ou réunion de deux ensembles A et B est l'ensemble qui contient tous les éléments qui appartiennent à A ou appartiennent à B. On note l'union de A et B A ∪ B. En notation symbolique, c'est :

Par exemple l'union des ensembles A={1,2,3} et B={2,3,4} est l'ensemble {1,2,3,4}.

En algèbre booléenne, l'union est associée à l'opérateur logique ou inclusif.

On généralise ce concept à une famille d'ensembles . La réunion ou union des ensembles membres de cette famille est l'ensemble des éléments x pour lesquels il existe un tel que . On le note alors .

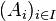
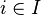
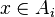
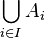
Propriétés algébriques

• L'union est associative, i.e. pour des ensembles A, B et C quelconques, on a :

(A ∪ B) ∪ C = A ∪ (B ∪ C)

• L'union est commutative, i.e. pour des ensembles A et B quelconques, on a :

A ∪ B = B ∪ A

• L'intersection est distributive sur l'union, i.e. pour des ensembles A, B et C quelconques, on a :

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)