Tribu (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Tribu engendrée par un ensemble de parties
Si
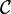
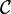
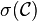
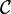
On prouve l'existence de
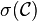
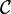
Exemples :
- Soit
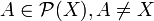
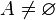
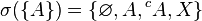
- Soit
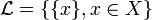

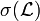
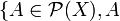
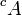
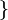
On dispose d'un procédé un peu plus « constructif » de production de
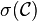
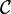
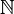
Cardinalité des tribus
Pour
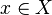
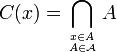
En utilisant seulement la stabilité de


Ce concept permet notamment de prouver la proposition suivante :
Proposition — Toute tribu infinie a au moins la puissance du continu.
Démonstration : Supposons infinie la tribu


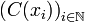
Pour tous indices
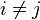
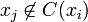
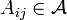
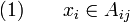
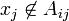
On définit alors une application
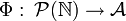
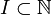
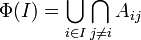
En utilisant (1), on vérifie que
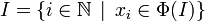
La conjonction de ce résultat et de la construction d'une tribu engendrée par récurrence transfinie permet de prouver un résultat plus précis lorsqu'on suppose la tribu dénombrablement engendrée :
Théorème — Soit
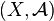
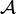
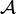
Constructions de tribus
Tribu image réciproque
Proposition et définition — Soit
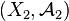
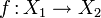
L'ensemble
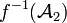
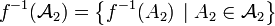
est une tribu sur X1. On l'appelle tribu image réciproque ou tribu engendrée par f.
Comme indiqué un peu plus bas, ceci permet notamment de restreindre une tribu à un sous-ensemble de son univers X. Le lemme de transport est un résultat simple mais utile pour manipuler une image réciproque de tribu définie par une partie génératrice, par exemple une tribu borélienne.
Lorsque plusieurs fonctions partent de
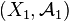
Tribu image
Proposition et définition — Soit
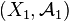
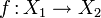
L'ensemble
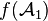
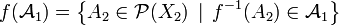
est une tribu sur X2. On l'appelle tribu image.
Tribu trace
Proposition et définition — Soit
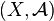
L'ensemble :
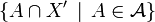
est une tribu sur X'. On l'appelle tribu trace.
La vérification directe est immédiate, mais on peut aussi s'apercevoir que c'est un cas particulier de tribu image réciproque, en l'espèce sous l'injection canonique de X' dans X.
Tribu produit
Définition — Soit
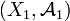
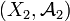
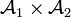
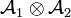
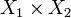
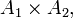
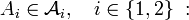
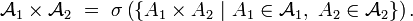
La définition de la tribu produit est le préalable à celle de la mesure produit dont l'usage permet de généraliser à des espaces abstraits les intégrales multiples.
Le concept se généralise à un produit d'une famille infinie d'espaces mesurables.
Tribu complétée
Proposition et définition — Soit
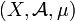
L'ensemble
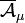
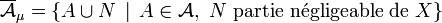
est une tribu sur X. On l'appelle tribu complétée.
Le résultat de la complétion dépend de μ, puisque la notion de partie négligeable n'a de sens que vis-à-vis d'une mesure bien précisée.
La construction généralise dans un cadre abstrait la situation de la tribu de Lebesgue relativement à la tribu borélienne de


















































