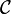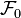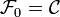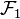Tribu engendrée - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Étant donné un ensemble 
de parties d'un même ensemble X, la tribu engendrée par est la plus petite tribu (au sens de l'inclusion) contenant . On la note 
.
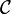
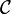
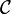
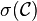
Définitions
Tribu engendrée par un ensemble de parties
Proposition et définition — Soit X un ensemble et un ensemble de parties de X. Il existe une plus petite tribu sur X (pour l'inclusion) qui contienne . On l'appelle la tribu engendrée par , et on la note .
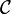
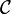
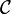
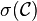
On prouve facilement l'existence de en la définissant comme l'intersection de toutes les tribus sur X qui contiennent (cette intersection a un sens, puisqu'au moins une telle tribu existe, à savoir la tribu dite discrète formée de toutes les parties de X).
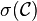
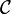
Tribu engendrée par une famille d'applications
Définition — Soit X un ensemble, I un ensemble d'indices et soit pour chaque 
un espace mesurable 
et une application 
.
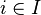
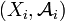
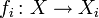
On appelle tribu engendrée par la famille 
la famille engendrée par la réunion des tribus image-réciproques 
. On la note 
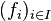
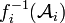
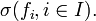
On vérifie facilement que :
- la tribu engendrée est la plus petite tribu qui rende simultanément mesurables toutes les applications fi.
- en notant
, pour pour toute application g d'un espace mesurable 
vers 
, g est mesurable si et seulement si chaque 
l'est.
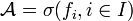
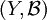
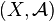
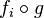
Construction transfinie
Un procédé de construction récurrence transfinie permet plus généralement une description de la tribu engendré par une partie 
. Il a été appliqué dès 1898 par Émile Borel pour définir la famille qu'on appelle aujourd'hui tribu borélienne.
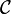
Pour le décrire posons d'abord une notation : pour 
ensemble de parties d'un ensemble X, on notera 
l'ensemble des unions dénombrables d'éléments de et 
l'ensemble des intersections dénombrables.
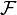
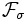
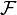
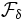
Une première idée, non concluante, pourrait être la suivante : on part de l'ensemble 
composé des éléments de et de leurs complémentaires. Pour construire de nouveaux éléments de la tribu engendrée, on applique aux parties qui figurent dans la classe les opérations d'union dénombrable et d'intersection dénombrable : on obtient ainsi une nouvelle classe 
. On recommence l'opération en posant 
et ainsi de suite par récurrence. On pourrait espérer que la réunion de la suite croissante des 
réponde à la question : elle n'est évidemment pas vide, chaque est stable par complémentaire, les opérations de réunion ou d'intersection infinie envoient dans 
. Mais ce dernier point n'entraîne pas qu'elles envoient la réunion des dans elle-même : qu'on songe à une possible suite d'ensembles 
où chaque Ai est un élément de 
. Rien ne permet d'assurer que sa réunion ni son intersection sera elle aussi dans l'un des .
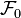
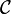
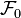
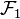
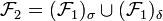
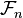
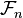
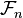
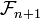
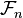
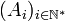
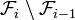
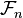
Cette idée peut pourtant être exploitée mais à condition de pousser plus loin la construction en effectuant une récurrence transfinie. On définit pour chaque ordinal α un ensemble de parties de Ω selon la procédure suivante :
- est l'ensemble composé des éléments de et de leurs complémentaires. ;
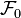
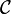
- pour tout ordinal α,
;
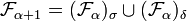
- pour tout ordinal limite β,
.
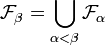
Notons alors ω1 le premier ordinal non dénombrable, on vérifie alors facilement que :
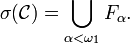
- L'inclusion dans le sens
est facile - par récurrence transfinie on constate aisément que pour tout ordinal α, 
est inclus dans . Dès lors l'ensemble 
l'est aussi.
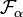
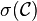
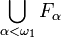
- Pour le sens
, on remarque que 
et qu'il suffit donc de s'assurer que ce dernier ensemble est lui-même une tribu pour garantir qu'il contiendra . Or il est non vide de façon évidente, stable par complémentarité parce que chaque l'est (récurrence transfinie facile, à l'aide des lois de De Morgan pour le passage à un ordinal successeur), seule la stabilité par réunion dénombrable demande un peu d'attention. Soit donc 
une suite d'éléments de ; pour chaque i notons αi le plus petit ordinal tel que 
, et posons enfin 
. Comme réunion dénombrable d'ordinaux dénombrables, β est lui-même un ordinal dénombrable - il est alors aisé de vérifier que 
. La stabilité par réunion dénombrable est prouvée.
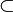
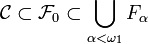
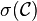
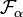
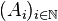
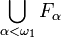
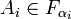
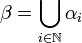
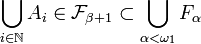
Lorsque X est un espace topologique métrisable et la topologie sur X cette construction admet des variantes. Il n'est ici pas nécessaire d'initialiser la récurrence en mêlant ouverts et fermés comme on le ferait si on suivait le mode d'emploi donné plus haut pour définir . En effet la métrisabilité garantit que tout fermé est un Gδ (et tout ouvert un Fσ) donc si on initialise la récurrence en prenant 
on retrouve les fermés dès ; on peut bien sûr symétriquement choisir une initialisation à partir de l'ensemble des fermés. La considération conjointe de ces deux itérations parallèles conduit à l'introduction de notations standardisées, ces familles croissantes de classes jouant un rôle important en théorie descriptive des ensembles : c'est ce qu'on appelle la hiérarchie de Borel.