Tribu engendrée - Définition
La liste des auteurs de cet article est disponible ici.
Exemples
- Soit
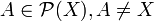
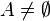
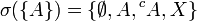
- Soit
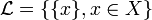
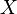
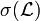
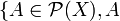
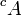
- Dans un espace topologique, la tribu engendrée par les ouverts (ou, ce qui revient au même, par les fermés) est appelée la tribu borélienne.
- Étant donné un espace mesuré
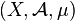
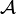
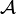
Extensions de fonctions d'ensembles
Dans les problèmes évoqués dans cette section, on dispose d'informations sur une fonction μ définie sur une classe
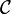
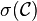
Problèmes d'unicité
Dans cette problématique on sait que μ est la restriction d'une mesure ; on veut s'assurer disposer avec cette restriction d'assez d'informations au sujet pour caractériser complètement μ.
Il s'avère que la connaissance d'une mesure sur une partie génératrice d'une tribu ne permet pas en général sa reconstitution : deux mesures peuvent coïncider sur une classe
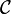
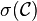
Exemples :
- Sur Ω = {a} singleton, on donne
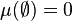
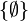
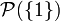
- Même si on sait que la mesure à reconstituer est une mesure de probabilité sur la tribu engendrée, sa reconstitution n'est pas forcément possible. Soit Ω = {aa,ab,ba,bb} un ensemble à quatre éléments. L'ensemble de parties {{aa,ab},{aa,ba}} est manifestement générateur de la tribu discrète. Pourtant si on sait qu'une mesure de probabilité vérifie les deux conditions P({aa,ab}) = 1 / 2 et P({aa,ba}) = 1 / 2, deux reconstitutions au moins en sont-elles envisageables : peut-être tous les tirages sont-ils équiprobables, ou peut-être seuls les tirages aa et bb sont-ils possibles avec équiprobabilité.
Pour une mesure de probabilité, il existe toutefois une condition suffisante simple garantissant que ses valeurs sur
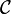
Lemme d'unicité des mesures de probabilité — Deux mesures de probabilité
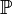
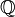
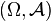
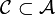
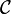
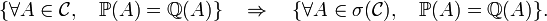
La démonstration est immédiate à partir d'un lemme, dit « lemme de classe monotone » ou « théorème lambda-pi de Dynkin » :
Lemme de classe monotone — Soit X un ensemble et
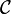
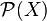
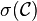
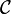
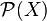
- contienne X ;
- soit stable par différence de parties emboîtées : si
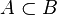
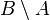
- soit stable par réunion dénombrable croissante.
Un exemple positif d'utilisation des résultats de cette section est la caractérisation des mesures de probabilité par leur fonction de répartition, l'ensemble des intervalles de la forme
![]-\infty,x], x\in\R](https://static.techno-science.net/illustration/Definitions/autres/7/7b0912906339d3a9d9703be98cdbf7c7_b6a95d2f1bafac3b991cdc018275d015.png)
Problèmes d'existence
Ici le problème est de généraliser dans un cadre abstrait les idées qui ont abouti à la définition de la mesure de Lebesgue sur la droite réelle : étant donné une classe d'ensembles
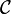
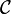
Une réponse est apportée par le théorème d'extension de Carathéodory. En voici un énoncé possible (dans cet énoncé, on entend par « mesure » sur un anneau d'ensembles une application de cet anneau vers
![[0,+\infty]](https://static.techno-science.net/illustration/Definitions/autres/0/0dc741c63f937db1bb20cfbcb633b71c_f7f63f9efef126b9fedf2310058eec21.png)
Théorème — Toute mesure sur un anneau d'ensembles admet au moins un prolongement en une mesure définie sur la tribu engendrée par cet anneau.

















































