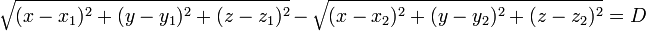Triangulation - Définition

Introduction

En géométrie et trigonométrie, la triangulation est une technique permettant de déterminer la position d'un point en mesurant les angles entre ce point et d'autres points de référence dont la position est connue, et ceci plutôt que de mesurer directement la distance entre les points. Ce point peut être considéré comme étant le troisième sommet d'un triangle dont on connaît deux angles et la longueur d'un côté.

Mathématiques

En topologie, une triangulation d'un espace topologique X est un complexe simplicial K homéomorphe à X, et un homéomorphisme h:K→X. La triangulation est utile pour déterminer les propriétés d'un espace topologique.

En géométrie, une triangulation est une façon de découper une forme géométrique (un plan, un polygone) en une collection de triangles. Un exemple classique est la triangulation de Delaunay.

La triangulation est aussi le processus qui permet de déterminer une distance en calculant la longueur de l'un des côtés d'un triangle, et en mesurant deux angles de ce triangle. Cette méthode utilise des identités trigonométriques.

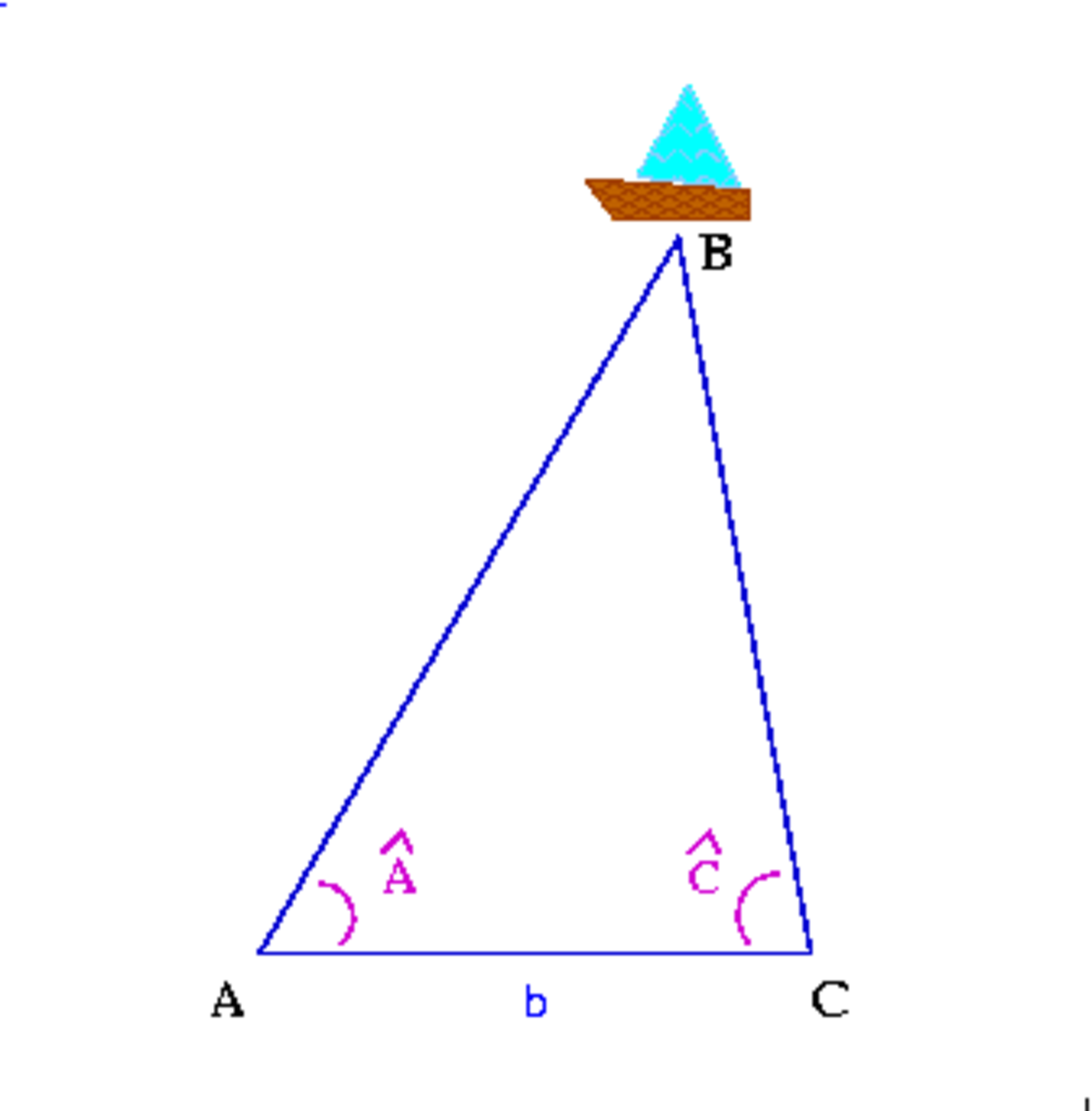
Six-cent ans avant l'ère chrétienne, Thalès mit au point une méthode pour évaluer la distance d'un bateau en mer à la côte. Pour avoir une mesure approximative de cette distance, il plaça deux observateurs A et C sur le rivage éloignés d'une distance b connue. Il demanda à chacun d'entre eux de mesurer l'angle que font les droites passant par le bateau B et l'un d'entre eux, et la droite passant par les deux observateurs :

La méthode a un intérêt si nous voulons déterminer de grandes distances ; mais dans ce cas nous devons placer les deux observateurs suffisamment éloignés l'un de l'autre, pour que les mesures d'angle soient plus précises.

Les propriétés souvent utilisées pour la triangulation sont :

• La somme des angles d'un triangle est égale à π radians (180 degrés).
• La loi des sinus
• Le théorème d'Al-Kashi
• Le théorème de Pythagore

Applications

Triangulation par relevé des directions

La triangulation est utilisée dans divers secteurs, comme la survie, la navigation, l'astronomie, dans l'armement (fusées).

Un navire peut ainsi connaître sa position en relevant la direction d'observation (angle par rapport au Nord) de deux points distants (par exemple un clocher d'église, un phare) ; il lui suffit alors, sur une carte, de tracer les droites passant par les points observés et ayant la direction relevée, l'intersection de ces droites étant la position du navire. Pour lever les imprécisions de mesure, on utilise généralement 3 points de repères, appelés amers. C'est la Navigation par relèvements.

Dans le cas d'ondes électromagnétiques (par exemple des ondes radio), la position peut se déterminer avec une antenne directionnelle (c'est-à-dire une antenne ne captant que les ondes venant d'une direction donnée) ; l'orientation pour laquelle le signal est le plus fort donne la direction de l'émetteur, il suffit alors de faire plusieurs relevés pour avoir la position de l'émetteur (radiogoniométrie). Cette méthode était par exemple utilisée durant l'occupation allemande de la France pour détecter les émetteurs radio pirates.

Position statique

On vise deux points, et on relève les directions de visée. Il suffit ensuite de tracer, sur une carte, une droite passant par le point visé et ayant la direction relevée. L'intersection des droites donne la position.

On a deux sommets du triangle (les amers) et la direction des deux côtés ne joignant pas ces sommets (relèvements), ce qui permet de déterminer complètement le triangle.

Si l'on effectue trois relevés, on devrait obtenir un point de concurrence unique des trois droites. Dans la pratique, les imprécisions — sur la visée, sur la lecture de l'angle, sur le tracé de la droite — font que l'on obtiendra un triangle, la dimension du triangle donnant une estimation de la précision de la mesure. On peut raisonnablement (si les angles sont à 120° l'un de l'autre) prendre pour position le barycentre de ce triangle, et pour erreur la distance entre ce centre et le point le plus éloigné.

Véhicule en mouvement

Dans le cas d'un véhicule en mouvement, il faut prendre en compte le déplacement du véhicule. Il faut pour cela connaître la direction et la vitesse du véhicule. La direction du mouvement est donnée par le compas ; dans le cas d'un voilier, la vitesse peut être estimée à partir de la vitesse du vent et du courant.

Si la vitesse est lente et que les relevés sont faits de manière proche (cas de la navigation maritime), on peut négliger ce phénomène, par contre, il faut noter l'heure du relevé.

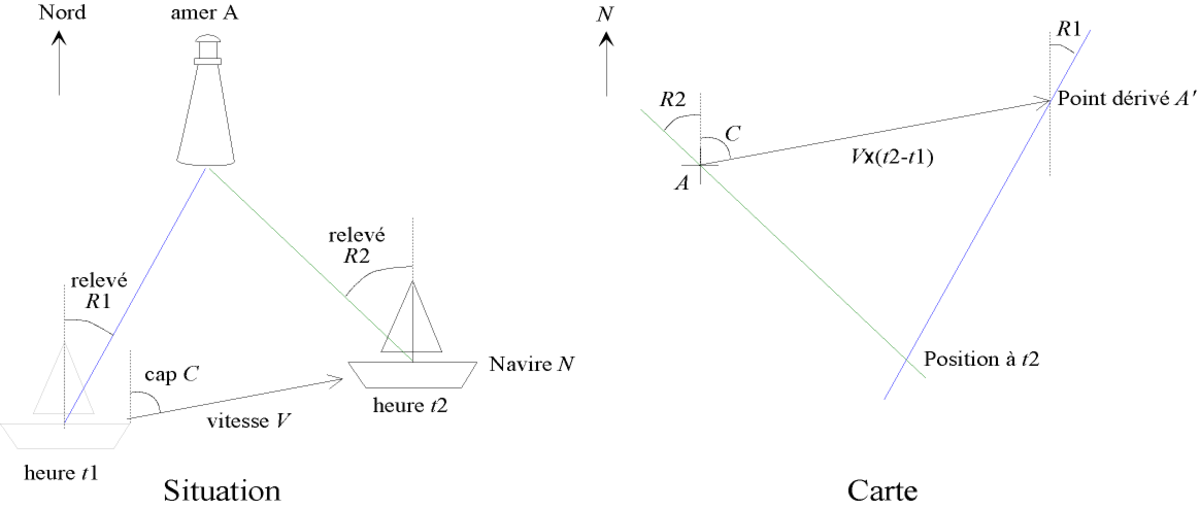
La connaissance de ce mouvement permet de faire un relevé avec seulement un amer, par exemple dans le cas d'une navigation par temps de brouillard où seul un lieu caractéristique serait visible par intermittence. On relève alors les directions et les heures du relevé.

On a ainsi un sommet du triangle (l'amer), les directions de deux côtés (les deux relevés), et la direction et la longueur du troisième côté (trajectoire du bateau), ce qui permet de déterminer complètement le triangle.

Voir l'article Navigation par relèvements > Positionnement avec un seul amer

Triangulation par relevé des distances

On peut relever une position en estimant la distance par rapport à trois points. Si l'on prend deux points de référence, on a deux sommets et les longueurs des côtés ne joignant pas ces sommets, ce qui définit deux triangles ; le point du relevé se trouve au troisième sommet de l'un de ces triangles. L'adjonction d'un troisième point de référence permet de déterminer lequel des deux sommets est le bon.

Utilisation de l'intensité d'un signal

Avec une onde électromagnétique, on peut utiliser l'intensité du signal collectée par une antenne non directionnelle. Si le milieu de propagation est homogène et isotrope, l'intensité est inversement proportionnelle au carré de la distance (l'énergie se répartit sur une sphère grandissante) et donc diminue avec l'augmentation de la distance source-récepteur. L'intensité permet donc d'estimer la distance, et donc de situer l'émetteur sur un cercle centré sur le récepteur. Un deuxième récepteur permet de tracer un second cercle, l'émetteur se trouve donc à l'intersection des deux cercles ; un troisième récepteur permet de déterminer lequel des deux points d'intersection est le bon (ou bien la logique, un navire ne peut pas se trouver sur les terres). Cette méthode est aussi utilisée en sismologie pour connaître la position de l'épicentre d'un séisme ; on considère alors l'intersection de sphères (on n'a plus la contrainte d'un émetteur situé en surface), et il faut corriger les calculs de l'hétérogénéité du milieu (variation de l'indice de réfraction en fonction de la profondeur, réflexion et réfraction sur le manteau...).

Si l'on ne connaît pas l'intensité de l'émetteur ni le rendement des récepteurs, il faut se trouver les positions pour lesquelles le signal est reçu avec la même intensité ; l'émetteur se trouve alors sur la médiatrice du segment constitué par les deux récepteurs. On peut localiser la source avec un deuxième relevé, à l'intersection des deux médiatrices. La méthode des médiatrices, légèrement modifiée, est utilisée en sauvetage-déblaiement pour localiser des victimes ensevelies avec un géostéréophone.

Utilisation de la vitesse de propagation d'un signal

Si l'on a des événements émettant un signal, alors en constatant le décalage dans l'arrivée des signaux, on peut déterminer la différence de distance entre les événements et les récepteurs, à condition de connaître la vitesse de propagation du signal.

Si le récepteur est lui-même synchronisé avec les émetteurs, on peut alors déterminer directement le temps de trajet et donc la distance entre émetteurs et récepteur.

Par exemple, pour localiser un séisme, on a un événement unique générant le signal, le séisme, et plusieurs stations réceptrices synchronisées, les sismographes. L'onde sismique arrive à des moments différents aux sismographes. Le foyer du séisme (hypocentre) est à une distance d_i du sismographe i.

Le foyer et deux sismographes forment un triangle ; on connaît deux sommets S₁ et S₂ du triangle (les sismographes), de coordonnées (x₁,y₁,z₁) et (x₂,y₂,z₂), et la différence de longueur D entre les deux côtés ne joignant pas ces sommets. Le troisième sommet du triangle est donc sur une surface vérifiant

d(M,S₁) − d(M,S₂) = D

soit

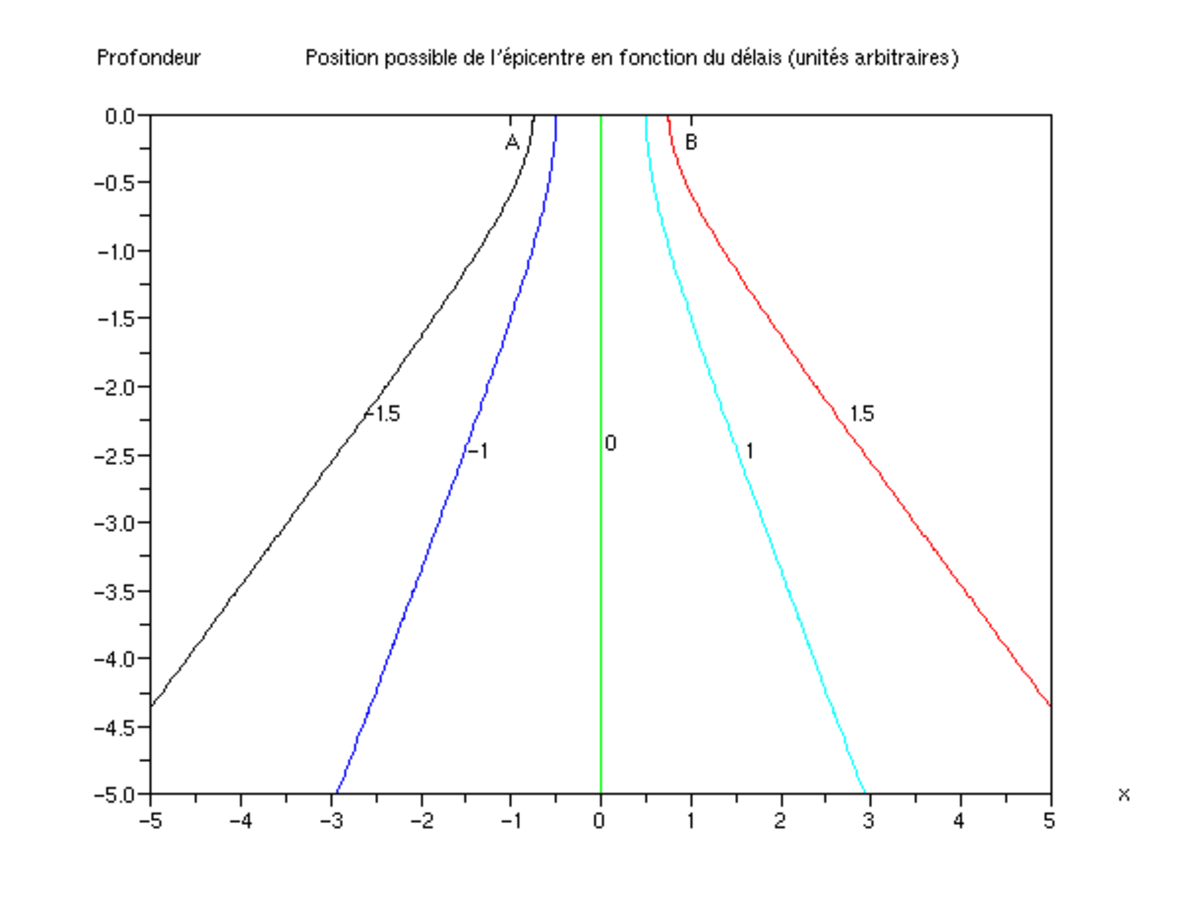
qui est l'équation d'un hyperboloïde. Il faut suffisamment de sismographes pour définir trois surface, le point de concurrence de ces surfaces donnant le foyer du séisme.

On a plusieurs types d'ondes sismiques voyageant à des vitesses différentes, ce qui permet de faire plusieurs déterminations. Toutefois, le problème est rendu complexe car :

• les ondes ne voyagent pas en ligne droite : la vitesse de propagation dépend de la pression donc de la profondeur sous le sol, on a un phénomène de réfraction avec variation continue d'indice ;
• il y a des discontinuités, les ondes subissent donc des réflexions ;
• les ondes de cisaillement (type S) ne voyagent pas dans le liquide, donc ne peuvent pas passer par le noyau terrestre.

Voir l'article Mesure en sismologie.

On peut également localiser d'autres événements comme par exemple une forte explosion (essai nucléaire, catastrophe industrielle de grande ampleur comme la catastrophe de l'usine AZF...).

Pour la navigation par satellite (système type GPS), on a plusieurs émetteurs synchronisés et un récepteur unique à l'endroit à localiser.