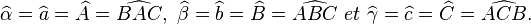Triangle - Définition

Introduction

En géométrie euclidienne, un triangle est une figure plane, formée par trois points et par les trois segments qui les relient. La dénomination de « triangle » est justifiée par la présence de trois angles dans cette figure, ceux formés par les segments entre eux. Les trois points sont les sommets du triangle, les trois segments ses côtés, et les trois angles ses angles.

Le triangle est une figure géométrique élémentaire, à l'instar du point, de la droite ou du cercle. Il constitue depuis l'Antiquité une réserve inépuisable de propriétés, d'exercices et de théorèmes mathématiques de difficultés variées. La plupart des propriétés et définitions énoncées dans cet article étaient déjà énoncées, environ 300 ans avant Jésus-Christ, dans les Éléments d'Euclide.

Pour l'étude du triangle dans d'autres géométries, voir Triangle (géométries non euclidiennes).

Conventions d'écriture

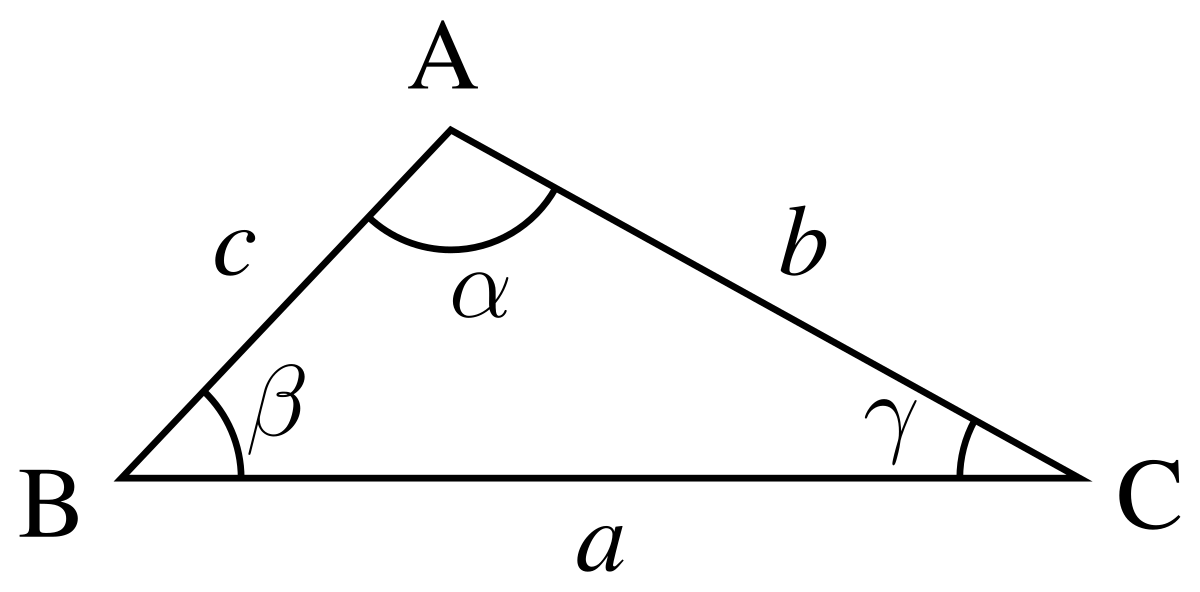
Les points intéressants d'une figure géométrique, tels que les sommets d'un polygone, sont habituellement désignés par des lettres latines majuscules : ''A, B, C, ... Un triangle est alors nommé, comme tout autre polygone, en donnant successivement le nom de ses sommets, par exemple ABC. L'ordre de citation des sommets n'a pas d'importance, car tous les segments dont ces sommets sont les extrémités sont des côtés du triangle.

Les côtés du triangle, justement, sont dénommés, comme tous les segments, par leurs extrémités : AB, BC, et AC dans notre exemple. Pour nommer la longueur d'un côté, on utilise en général le nom du sommet opposé, converti en minuscule latine : a pour BC, b pour AC, c pour AB.

La notation générale pour l'angle entre deux segments OP et OQ partageant l'extrémité O est

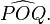
On peut aussi utiliser une lettre minuscule, grecque le plus souvent, surmontée d'un accent circonflexe (en toute rigueur, les grandeurs devraient être désignées par des majuscules et leur mesure par des minuscules, mais on recourt souvent aux mêmes noms pour les deux afin d'alléger les notations). Dans le cas d'un triangle, l'angle entre deux côtés peut encore, par tolérance et en l'absence d'ambiguïté, être désigné par le nom du sommet commun surmonté d'un accent circonflexe. Bref, dans notre exemple, nous pouvons noter les angles :

Si on tolère de confondre un angle et sa mesure dans les énoncés ou les calculs, la notation correcte est par exemple :

°.

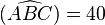
Nous utiliserons ces notations dans cet article.

Typologie des triangles

Lorsque les trois sommets d'un triangle sont alignés, on parle de triangle aplati. Il est équivalent de dire qu'un angle du triangle est plat (il mesure alors 180°) ou que deux angles du triangle sont nuls (ils mesurent 0°).

Les triangles admettant deux angles droits (de 90°) et un angle nul (de 0°) sont qualifiés de triangles en aiguille (cas particulier de triangle aplati). C'est un cas limite, car les angles droits ne sont pas correctement définis.

Dans tous ces cas, on parle de triangles dégénérés. Dans la suite de cet article, on suppose que les triangles ne sont pas dégénérés. Dans le cas des triangles dégénérés, de nombreuses propriétés usuelles des triangles sont fausses ou triviales.

Classement selon le type d'angles

Comme la somme des angles d'un triangle vaut 180°, un triangle ne peut pas comporter deux angles droits (mesurant 90°) ou obtus (mesurant plus de 90°). Il a donc au moins deux angles aigus. Si le troisième angle est :

• droit, on parle de triangle rectangle  ;
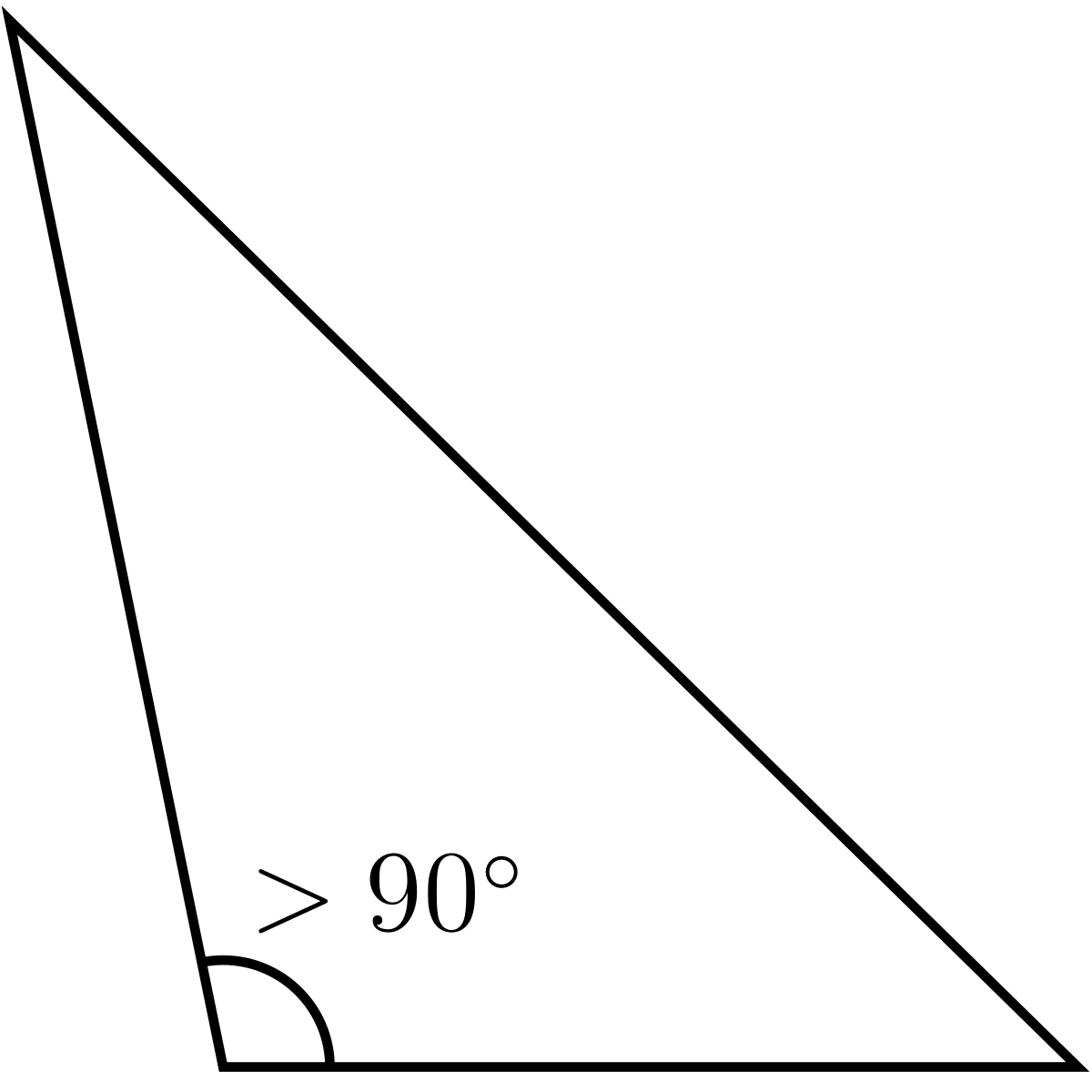
• obtus, on parle de triangle obtusangle ou ambligone (ou parfois de triangle obtus) ;
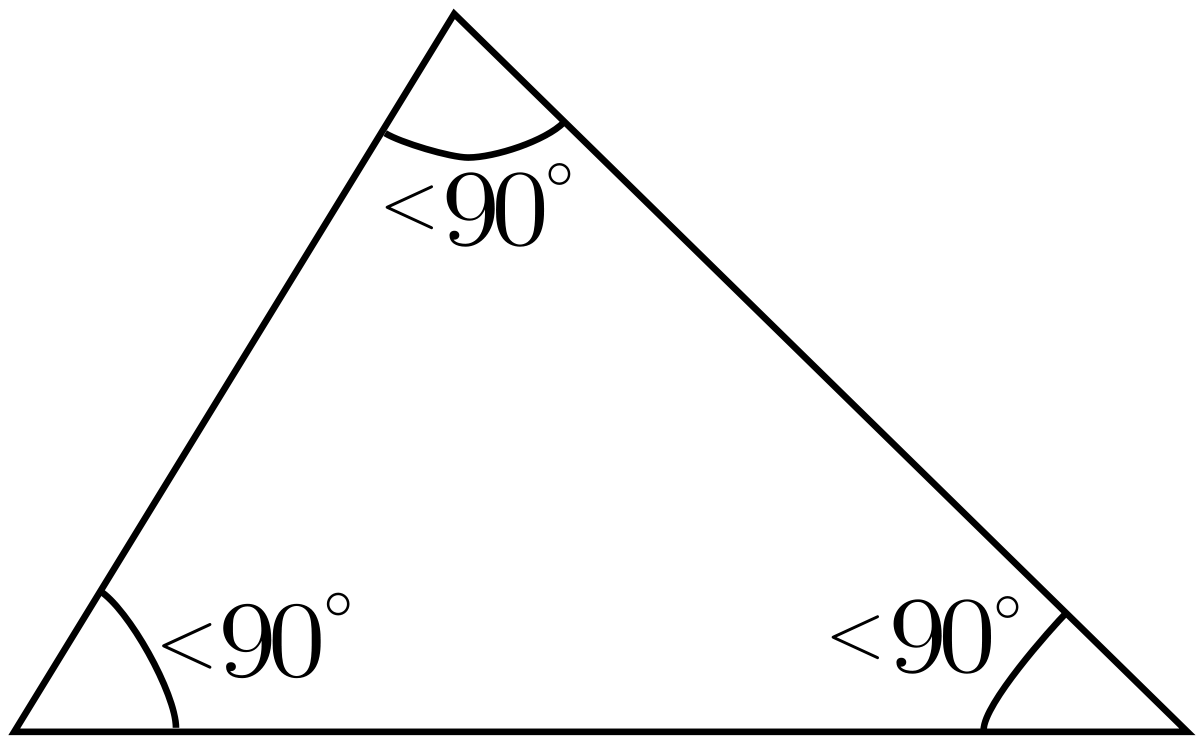
• aigu, on parle de triangle acutangle ou oxygone (ou de triangle aigu).

Triangle obtusangle ou ambligone

Triangle rectangle

Triangle acutangle ou oxygone

Classement suivant les symétries

Les triangles peuvent se classer suivant plusieurs types de symétries :

• suivant le nombre de côtés égaux ;
• suivant le nombre d'angles égaux ;
• suivant le nombre d'axes de symétrie présents ;
• suivant le type de symétrie présent.

En fait, tous ces classements sont équivalents.

Le triangle isocèle

Les trois propositions suivantes sont équivalentes :

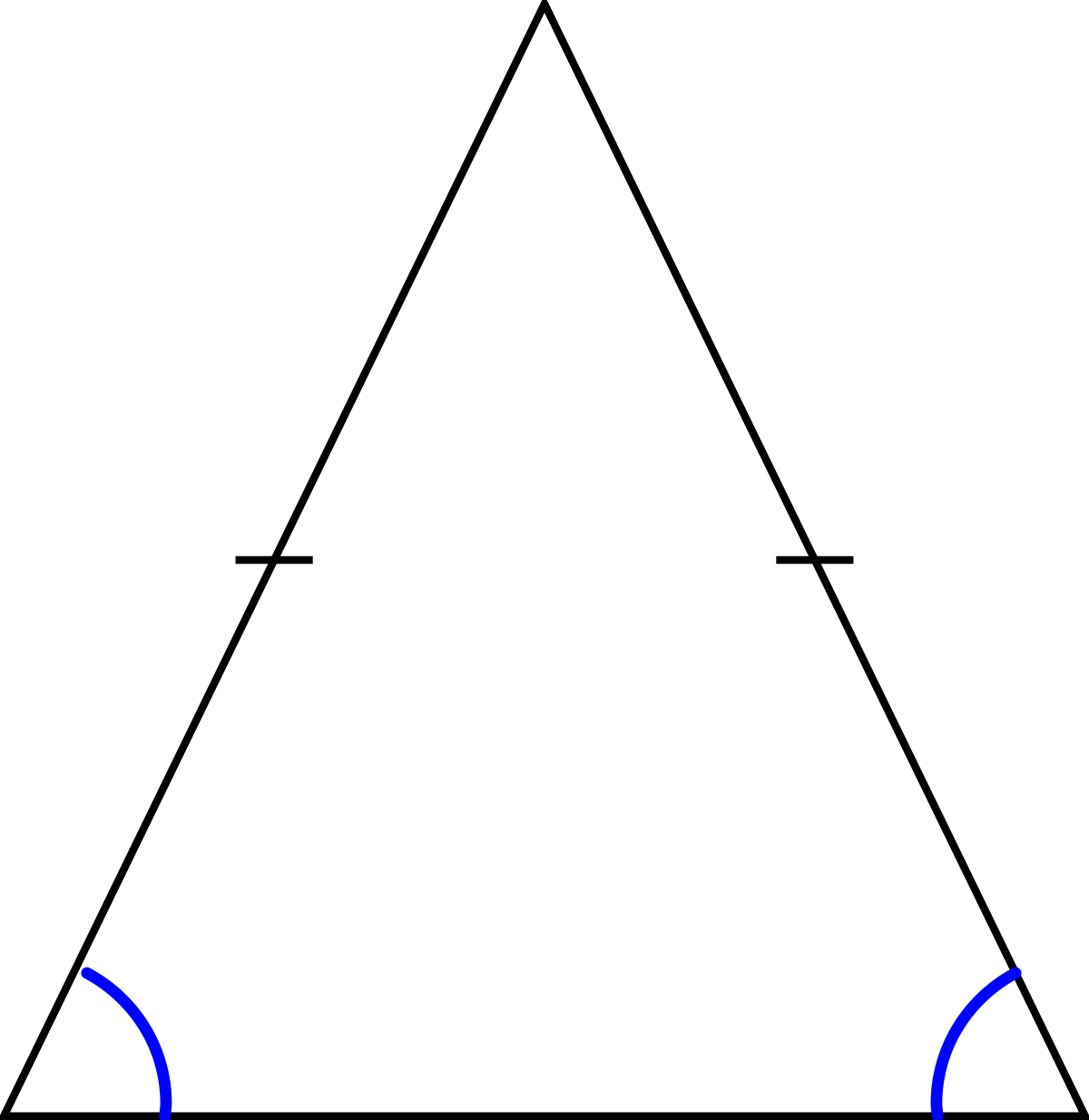
• Un triangle a deux côtés de même longueur.
• Un triangle a deux angles de même mesure.
• Un triangle a un axe de symétrie.

Dans ce cas le triangle est dit isocèle. (On peut aussi dire isoangle). Isocèle du grec iso = même et scèle = jambe

Lorsqu'un triangle ABC est tel que AC = AB (les deux côtés d'extrémité A sont égaux), alors on dit que le triangle est isocèle de sommet A et que A est le sommet principal du triangle. Le côté [BC], opposé à A, est appelé base du triangle.

Lorsqu'un triangle est isocèle en A, la hauteur issue de A est aussi la médiatrice et la médiane du côté [BC] et la bissectrice de l'angle en A.

Un triangle bisocèle est un triangle isocèle qui, lorsqu'il est « coupé » en deux par la bissectrice d'un de ses angles, forme deux triangles isocèles eux aussi. Il n'y a que deux cas de triangles bisocèles : le triangle d'or et le triangle isocèle rectangle.

Un triangle isocèle peut aussi se trouver dans la figure formée par un parallélogramme et ses diagonales : dans un rectangle, dans un losange ou dans un parallélogramme où la longueur d'un des côtés est la même que celle de la moitié d'une des diagonales.

Triangle équilatéral ou régulier

Les trois propositions suivantes sont équivalentes :

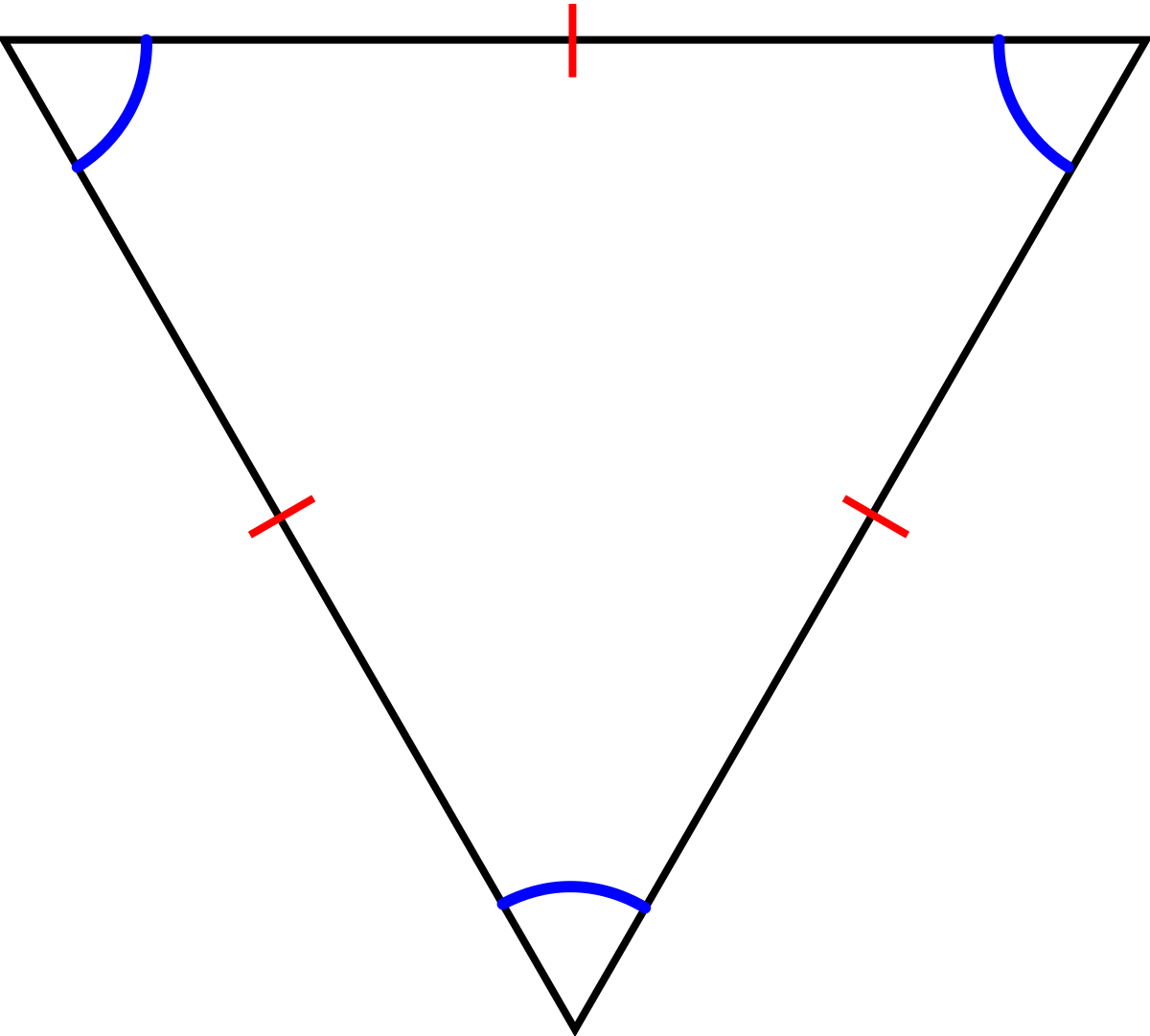
• Un triangle a ses trois côtés de même longueur.
• Un triangle a ses trois angles de même mesure.
• Un triangle a trois axes de symétrie.

Dans ce cas le triangle est dit équilatéral, ou équiangle, ou isopleure.

Les trois angles d'un triangle équilatéral mesurent 60°.

Pour déterminer un triangle équilatéral, on peut :

• montrer que le triangle a deux angles de 60°.
• ou montrer qu'il y a deux axes de symétrie.

Par ailleurs, toutes les droites remarquables (médiane, hauteur, bissectrice, médiatrice) relatives à un même côté sont confondues.

Le rapport entre la hauteur et le côté d'un triangle équilatéral est égal à , soit environ 0,866.

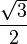
Le triangle équilatéral est celui qui présente la plus grande aire pour un périmètre donné. Ainsi, le triangle de plus grande aire et de périmètre égal à 3 est le triangle équilatéral de côté 1. Cette propriété est analysée dans l'article Isopérimétrie.

Triangle scalène ou irrégulier

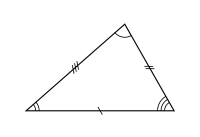
Un triangle scalène (du grec skalenos : boiteux, inégal, déséquilibré, oblique...) est un triangle dont :

• les trois côtés sont de longueurs différentes ;
• les trois angles sont de mesures différentes ;
• ou encore qui n'a pas d'axe de symétrie.

Les trois définitions ci-dessus sont équivalentes. Un tel triangle n'est bien sûr ni isocèle ni équilatéral, mais il peut être rectangle.

Triangle rectangle

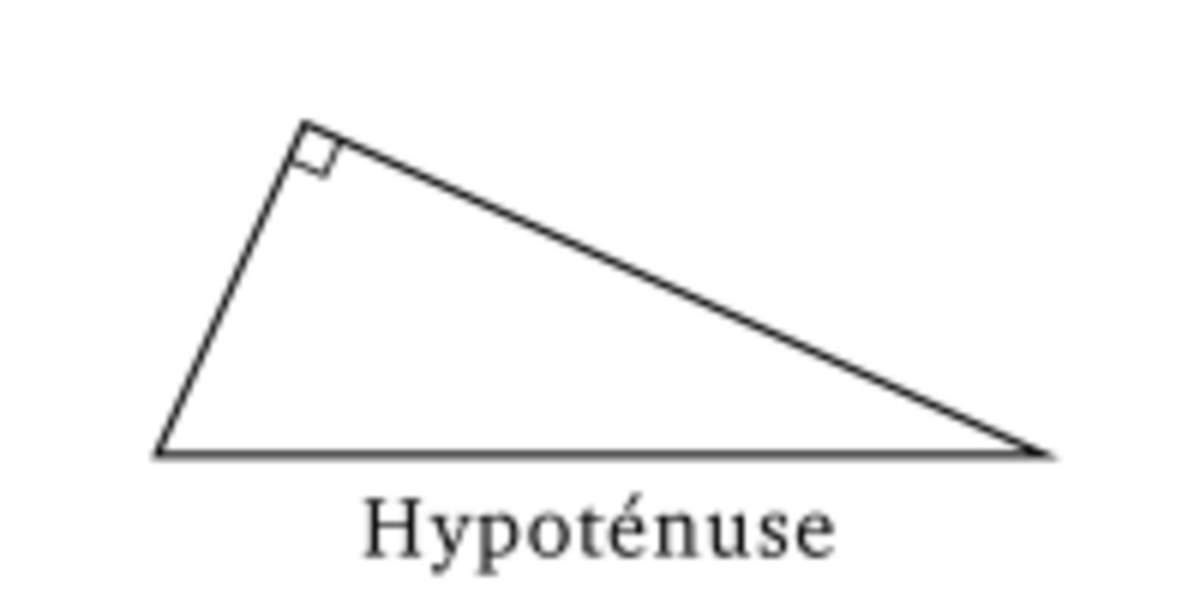
Lorsqu'un triangle présente un angle droit (mesurant 90°) on parle de triangle rectangle.

Parmi les nombreuses propriétés du triangle rectangle, citons le fameux Théorème de Pythagore : « Un triangle admet un angle droit si et seulement si le carré de la longueur d'un de ses côtés est égal à la somme des carrés des longueurs des deux autres côtés. »

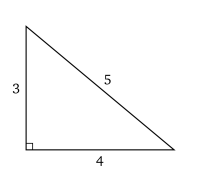
Le 'triangle 3-4-5 est un triangle rectangle dont les longueurs des côtés forment une progression . On peut remarquer que 5² = 3² + 4² (soit 25 = 9 + 16) : comme ce triangle vérifie la relation du théorème de Pythagore on peut en déduire qu'il est rectangle.

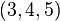
Ce cas particulier d'un triangle rectangle est connu depuis l'Antiquité. Il est facile à réaliser à l'aide d'une corde à treize nœuds : on l'utilisait pour tracer un angle droit au sol. Pour cette raison, on l'appelle aussi « triangle des arpenteurs ».

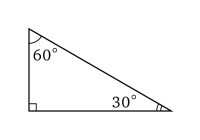
Le triangle 30-60-90 est un triangle rectangle dont les angles mesurent 30°, 60° et 90°, c'est-à-dire forment une progression . Les longueurs des côtés forment quant à eux une progression .

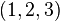
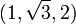
Ce triangle est parfois aussi appelé « triangle de l'écolier » : les équerres d'écolier ont parfois cette forme. On parle aussi de « triangle hémi-équilatéral ». Cette dernière appellation se justifie en remarquant qu'un triangle équilatéral peut être coupé suivant un axe reliant l'un de ses sommets au milieu du côté opposé, pour donner deux triangles 30-60-90 égaux.

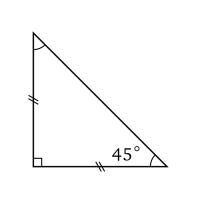
Un triangle peut être à la fois rectangle et isocèle. Dans ce cas, il l'est au même sommet. Ses deux angles aigus mesurent 45° (ou π/4 rad).

C'est le triangle obtenu en divisant un carré en deux suivant une diagonale, d'où le nom du triangle : « demi-carré ».