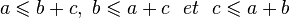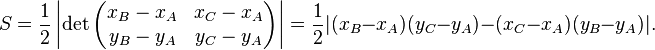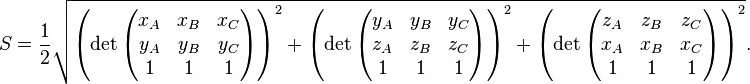Triangle - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés élémentaires
Un triangle peut être défini comme un polygone à trois côtés, ou encore comme un polygone à trois sommets.
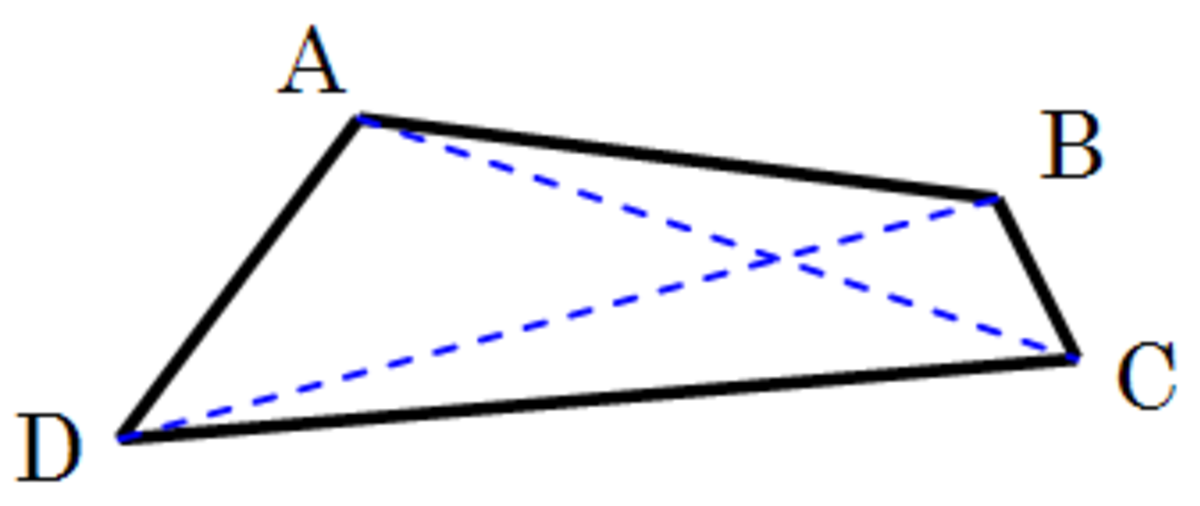
Après le point et le segment, le triangle est la figure polygonale la plus simple. C'est le seul polygone qui ne possède pas de diagonale propre. Dans l'espace, trois points non alignés définissent un triangle (et un plan). A contrario, si quatre points coplanaires forment un quadrilatère, quatre points non coplanaires ne définissent pas un polygone, mais un tétraèdre :
D'autre part, tout polygone peut être découpé en un nombre fini de triangles qui forment alors une triangulation de ce polygone. Le nombre minimal de triangles nécessaire à ce découpage est n − 2, où n est le nombre de côtés du polygone. L'étude des triangles est fondamentale pour celle des autres polygones, par exemple pour la démonstration du théorème de Pick.
Longueurs des côtés et inégalité triangulaire
Dans un triangle, la longueur d'un côté est inférieure ou égale à la somme des longueurs des deux autres côtés. Autrement dit, dans un triangle ABC, les trois inégalités suivantes sont vérifiées :
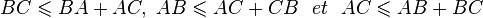
Cette propriété est caractéristique des triangles. Réciproquement, étant donnés trois nombres réels positifs a, b et c, si les trois inégalités :
sont vérifiées, alors il existe un triangle dont les côtés mesurent a, b et c.
Inversement, pour vérifier qu'il existe un triangle dont les longueurs des côtés sont a, b et c, il suffit en pratique de vérifier une seule des trois inégalités, celle où le plus long côté est à gauche de l'inégalité (ainsi, si max(a,b,c) = a , alors la seule inégalité à vérifier est :
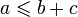
Le cas d'égalité de l'inégalité triangulaire permet de caractériser les points d'un segment : M est un point du segment [AB] si et seulement si : AM + MB = AB.
Enfin, la somme des longueurs des trois côtés d'un triangle est son périmètre.
Somme des angles
La somme des mesures des angles d'un triangle est égale à 180° ce qui équivaut à π radians.
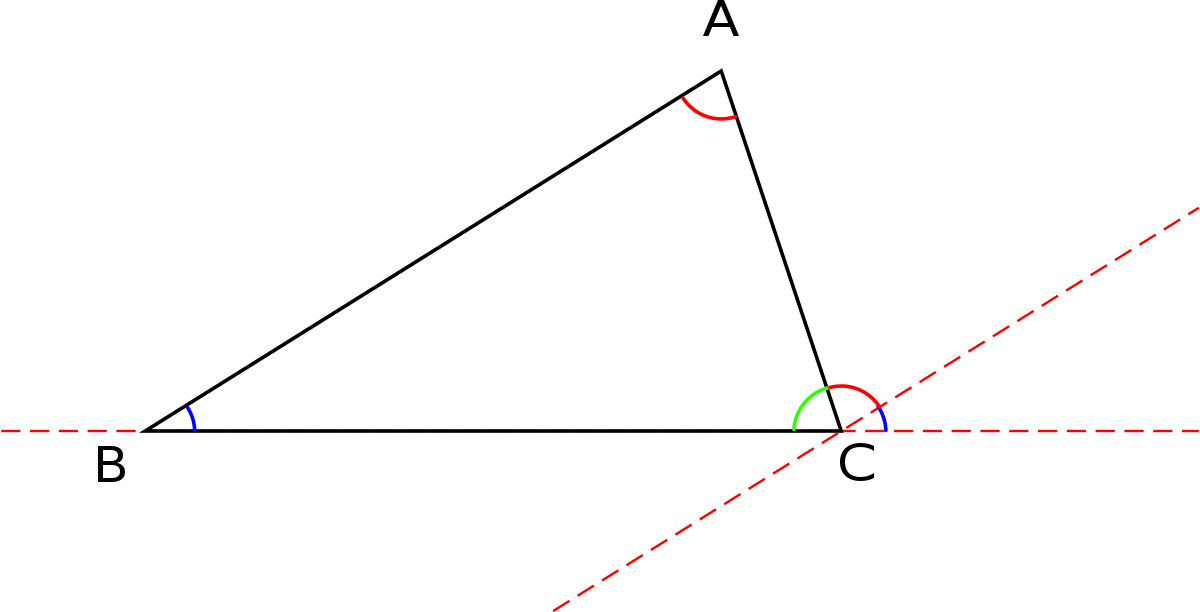
Euclide avait démontré ce résultat dans ses Éléments (proposition I-32) de la manière suivante : traçons la parallèle à la droite (AB) passant par C. Étant parallèles, cette droite et la droite (AB) forment avec la droite (AC) des angles égaux, codés en rouge sur la figure ci-contre (angles alternes-internes). De la même façon, les angles codés en bleu sont égaux (angles correspondants). D'autre part, la somme des trois angles de sommet C est l'angle plat. Donc la somme des mesures d'un angle rouge, d'un angle vert et d'un angle bleu est 180° (ou π radians). La somme des mesures des angles du triangle est donc 180°.
Cette propriété est un résultat de géométrie euclidienne. Elle n'est pas vérifiée en général en géométrie non euclidienne.
Propriétés métriques du triangle
Aire d'un triangle
L'aire d'un triangle est l'aire de la portion du plan qu'il enferme. Il existe plusieurs manières de la calculer, selon les informations dont on veut partir.
Calcul à partir d'une hauteur

Si le triangle est rectangle il est immédiat que son aire est
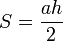
où a est la longueur d'un côté différent de l'hypoténuse et h la longueur de la hauteur issue de ce côté. Si le triangle n'est pas rectangle, la relation reste vraie, car le triangle se décompose en deux triangles rectangles (comme sur la figure).
À partir des longueurs des trois côtés
Pour une expression de l'aire d'un triangle dont les longueurs des côtés sont a, b et c et p le demi-périmètre [
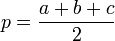
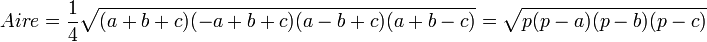
À partir des coordonnées des sommets
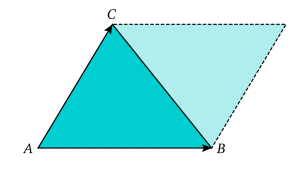
L'aire du parallélogramme défini par deux vecteurs
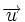
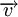
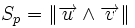
On peut calculer l'aire d'un triangle à partir de cette formule :
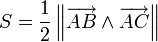
Un repère orthonormé étant donné, l'aire du triangle ABC peut être calculée à partir des coordonnées des sommets.
Dans le plan, si les coordonnées de A, B et C sont données par A(xA,yA), B(xB,yB) et C(xC,yC), alors l'aire S est la moitié de la valeur absolue du déterminant
L'aire du triangle ABC peut aussi se calculer à partir de la formule
Cette méthode se généralise en trois dimensions. L'aire du triangle ABC où A = (xA,yA,zA), B = (xB,yB,zB) et C = (xC,yC,zC) s'exprime comme
Relations métriques dans un triangle
Notations :
- p désigne le demi-périmètre du triangle :
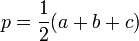
- S désigne l'aire de la surface du triangle ;
- R désigne le rayon du cercle circonscrit ;
- h désigne la hauteur relative au côté BC de longueur a ;
- r désigne le rayon du cercle inscrit ;
-
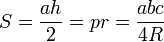
- (Formule de Héron) ;
-
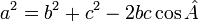
-
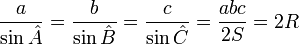
-
- Avec
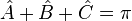
- Avec