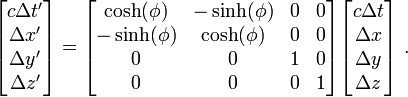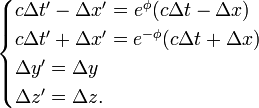Transformation de Lorentz - Définition

Introduction

Cet article présente les transformations de Lorentz sous un aspect technique. Le lecteur désireux d'obtenir des informations physiques plus générales à ce sujet pourra se référer à l'article relativité restreinte.

Hendrik Antoon Lorentz en 1916

Les transformations de Lorentz sont des transformations linéaires des coordonnées d'un point dans l'espace-temps de Minkowski, à quatre dimensions (trois d'espace et une de temps) et relativiste. On peut noter que la terminologie subit quelques variations : suivant que la théorie dans laquelle on travaille a trait ou non à la physique quantique, les termes « transformations de Lorentz » désignent des transformations qui peuvent être différentes.

Dans le cadre de la relativité restreinte, les transformations de Lorentz correspondent à la loi de changement de référentiel galiléen, sous laquelle les équations de la physique doivent être préservées, ainsi que la vitesse de la lumière, qui est la même dans tout référentiel galiléen. L'ensemble de ces transformations des coordonnées, aussi appelées transformations de Lorentz propres et orthochrones, est composé des transformations spécifiques à la relativité restreinte et des rotations dans l'espace à trois dimensions et forme le groupe de Lorentz.

Dans le cadre de la physique quantique relativiste, comme en Théorie quantique des champs, ce sont les transformations linéaires de l'espace-temps qui laissent les lois invariantes (en l'absence de charge électrique), ce qui englobe les précédentes et en amène d'autres pour former aussi un groupe : la symétrie T et la parité s'invitent parmi les transformations le Lorentz et, comme elles sont interprétées comme des changements de convention d'orientation des axes, elles ne sont pas utiles en relativité restreinte.

Dans chacun des deux cas l'ensemble des transformations désignées forme un sous-groupe du groupe de Poincaré.

Dans l'introduction à la publication, Deux Mémoires de Henri Poincaré sur la physique mathématique, Acta Matematica, Vol. 38, p. 293-308, en 1921, Hendrik Antoon Lorentz précise que c'est pour faire en sorte que les équations de Maxwell s'écrivent à l'identique dans tout référentiel galiléen que Henri Poincaré a introduit mathématiquement cette loi, en la baptisant du nom de Lorentz. Ce dernier en avait donné une version qu'il a, plus tard, lui-même jugée imparfaite.

Henri Poincaré

Les formules

Présentations les plus courantes

En relativité restreinte 

On considére deux référentiels et en translation rectiligne uniforme l'un par rapport à l'autre à la vitesse parallèle à l'axe des x, et on note respectivement et les trois coordonnées spatiales et le temps permettant de repérer un même événement observé depuis chacun de ces référentiels. De plus et représentent les différences de coordonnées entre deux événements observés depuis chacun de ces référentiels

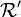
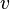
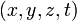
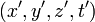
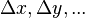
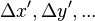
les transformations de Lorentz utilisées sont :

en posant et , on écrit :

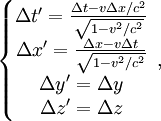
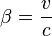
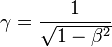
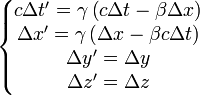
Sous forme matricielle, ces transformations de Lorentz s'écrivent :

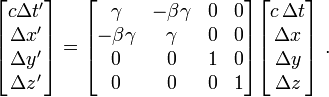
En physique quantique relativiste 

Les transformations de Lorentz qui doivent laisser invariantes les équations (en l'absence de charge électrique) sont :

avec indiquent s'il y a un changement d'orientation temporelle et/ou spatiale.

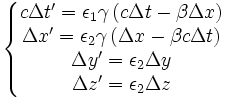
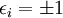
En considérant l'inversion temporelle T et l'inversion spatiale P, toute transformation utilisée en physique quantique est de la forme , avec une transformation de Lorentz de la relativité restreinte (orthochrone et propre) et .

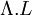
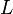
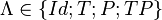
Le groupe des transformations propres et orthochrones étant connexe, la décomposition ci-dessus permet de voir que le groupe de Lorentz est formé de quatre composantes connexes, et que le groupe des transformations spéciales (i.e : de déterminant positif) est composé de deux composantes connexes.

Présentation comme rotation hyperbolique dans l'espace-temps de Minkowski

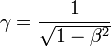
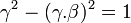
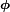
L'égalité montre que , ce qui permet de définir la rapidité entre les deux référentiels inertiels, à l'aide des fonctions hyperboliques, par et soit encore en utilisant .

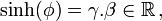
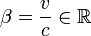
On obtient en écriture matricielle :

Les transformations de Lorentz sont présentées alors comme une rotation hyperbolique d'angle (la rapidité) dans l'espace-temps de Minkowski.

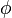
Présentation sous forme diagonalisée

Avec les définitions et propriétés des fonctions de la trigonométrie hyperbolique, on obtient une présentation un peu différente des transformations de Lorentz :

sous forme matricielle :

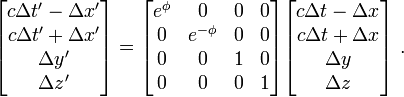
ce qui en est une forme diagonalisée avec des choix de repères dont deux axes forment l'intersection du cône de lumière avec le plan (Oxt), ou (Ox't') pour l'autre repère, et qui sont impossibles à matérialiser dans l'espace physique à trois dimensions.