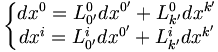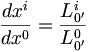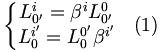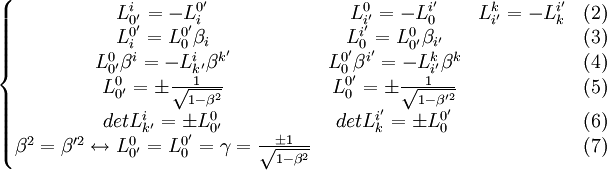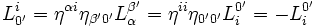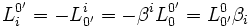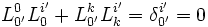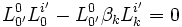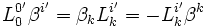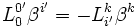Transformation de Lorentz - Définition
La liste des auteurs de cet article est disponible ici.
Différentes méthodes pour trouver les transformations
- Pour la relativité restreinte, Einstein a initié une méthode :
- À partir du principe de relativité et de l'invariance de la vitesse de la lumière par changement de référentiel, de l'homogénéité et de l'isotropie supposées de l'espace, et à l'aide d'une représentation géométrique d'une situation idéale où deux référentiels inertiels permettent de voir, mesurer les longueurs, et chronométrer le temps d'un référentiel à l'autre, on démontre les différentes formules par un système d'équations linéaires dont il faut trouver les coefficients. Les transformations non physiques sont parfois écartées sans détail par le choix de la solution positive dans une équation du second degré, choix dû à l'hypothèse physique de l'orientation des repères par une règle telle que celle de la main droite, illustrée par la représentation géométrique accompagnant le raisonnement.
- En physique quantique relativiste, comme en Théorie quantique des champs, les transformations utilisées sont définies comme les symétries de l'espace de Minkowski qui laissent inchangées les équations (en l'absence de charge électrique). Cela revient à déterminer les transformations linéaires laissant inchangé l'intervalle d'espace-temps : c'est une définition mathématique pour laquelle les changements de référentiel pour des observateurs ne sont que certaines de ces transformations et qui permet de les trouver toutes.
Cette méthode est aussi utilisée dans certains manuels de relativité restreinte, après avoir démontré que l'invariance de l'intervalle d'espace-temps par changement de référentiel découle directement des deux axiomes de la relativité restreinte, et en éliminant les transformations qui ne respectent pas la convention d'orientation pour les repères tridimensionnels (règle de la main droite, en général) et d'orientation de l'axe du temps vers le futur ; élimination faite de diverses manières, parfois marquées du sceau de l'évidence, et parfois plus justifiées.
La méthode géométrique
On suppose que l'espace-temps physique est un espace affine où les référentiels sont identifiés aux repères de cet espace affine. De plus on néglige les translations constantes entre les repères qui ne se manifestent que par des additions de nombres constants aux coordonnées. Donc, la transformation des coordonnées s'effectue au moyen d'un opérateur linéaire :
Soient deux référentiels

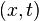

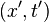
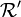
- Utilisation du principe de relativité :
- Par le principe de relativité, les coefficients de la transformation linéaire ne dépendent que de la vitesse relative entre les référentiels, et d'aucune considération extérieure à ces deux référentiels. Pour plus de précision, on devrait dire des vitesses relatives des référentiels, le sujet est abordé un peu plus loin.
- Première utilisation de la vitesse de la lumière :
- Si dans le référentiel

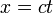
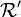
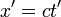
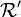
- Donc :
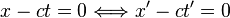
- Et comme x, t, x', t' sont liés par des relations linéaires à coefficients constants, on doit avoir
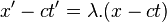
- Deuxième utilisation de la vitesse de la lumière :
- En considérant le déplacement d'un signal lumineux dans le sens des x négatifs, et en faisant le même raisonnement, on obtient :
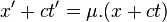
- Conclusion sur la vitesse de la lumière :
- En additionnant et soustrayant les deux égalités précédentes, on obtient :
-
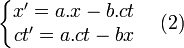
- avec :
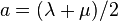
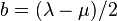
- Première utilisation de la vitesse relative des référentiels :
- Pour l'origine du référentiel
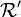
-
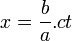
- En désignant par
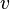
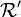

-
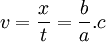
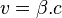
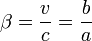
- On peut donc écrire :
-
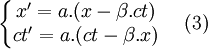
- Deuxième utilisation de la vitesse relative des référentiels :
- Pour l'origine du référentiel

-
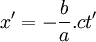
- En désignant par
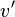

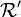
-
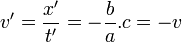
- Utilisation des hypothèses sur l'espace :
- Quand t = 0, on a
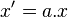

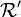
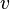
- Donc a dépend de la norme de la vitesse
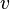
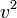
- Utilisation du principe de relativité :
- En inversant les rôles des référentiels

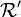
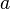
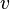
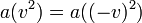
-
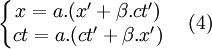
- En utilisant les deux équations du système (3) dans la première équation du système (4), on obtient
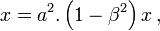
-
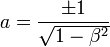
- Le signe + est choisi, sinon il y a changement dans d'orientation entre l'axe des x et l'axe des x', ce qui n'est pas le cas par hypothèse.
- Conclusion :
- Les transformations de Lorentz s'écrivent :
-
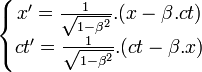
- Ce que l'on écrit souvent :
-
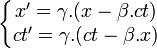
- Avec
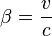
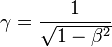
On trouvera une variante de cette démonstration où les principes de base (référentiels galiléens, vitesse de la lumière indépendante de celle de la source et principe de relativité) sont séparés sur Wikiversité
La méthode partant de l'invariance de la pseudo-norme
Les transformations de Galilée conservent le produit scalaire : :
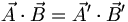
- Dans l'espace-temps de Minkowski, le tenseur métrique est :
-
![\eta_{\alpha\beta}=\left[\begin{matrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{matrix}\right]](https://static.techno-science.net/illustration/Definitions/autres/0/004c15717506cc50bd7be014733e16f5_a2d83851524bf8a77cc915e5cc851ade.png)
- Ce qui veut dire que l'on doit différencier les coordonnées covariantes, des coordonnées contravariantes. On définit la pseudo-norme : :ds2 = ηαβdxαdxβ = dxαdxα = c2dt2 − dx2 − dy2 − dz2
- Les transformations de Lorentz doivent conserver la pseudo-norme : :dxαdxα = dx'αdx'α
Les transformations de Lorentz doivent être linéaire à coefficients constants. Dans toute la suite, les indices primés correspondent aux coordonnées dans le référentiel
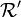
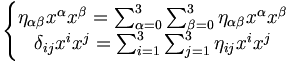
- Les transformations s'écrivent sous la forme matricielle :
-
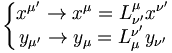
Les pseudo-produits scalaires sont invariants pas transformations de Lorentz :
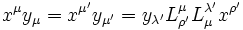
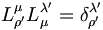
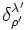
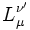
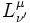
- xμxμ = xλ'xλ'
-
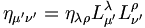
On en déduit que (detL)2 = 1 donc detL = 1 ou detL = − 1.
Terminologie : les transformations vérifiant
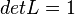
Les transformations s'écrivent alors :
On considère un corps au repos dans le référentiel
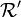
soit :
Ensuite il y a ces relations à démontrer :
Pour les expressions (2), il suffit d'utiliser la relation :
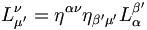
Pour les expressions (3) :
Pour les expressions (4), nous partons de
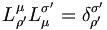
Pour les expressions (5) les relations de transformations du tenseur métrique donnent :
-
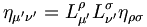
-
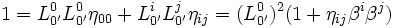
-
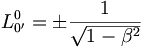
Pour les expressions (6) :
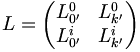
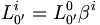
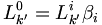
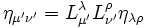
-
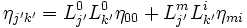
- or :
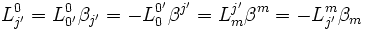
d'où :
-
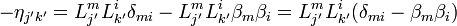
- On prend le déterminant :
-
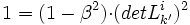
-
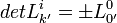
Pour les expressions (7) : Nous avons L' = L − 1 (matrices orthogonales), on a donc :
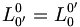
En se plaçant dans le cadre de la relativité restreinte, les transformations de Lorentz représentent des changements de référentiels :
- Il faut appliquer le principe de non retournement du temps, et donc écarter les valeurs négatives pour
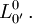
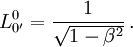
- Il faut appliquer le principe de non retournement de l'orientation spatiale (par la main droite en général), et donc écarter les cas où
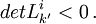
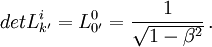
Ainsi, les transformations de Lorentz utilisées en relativité restreinte sont celles qui sont propres et orthochrones.