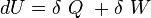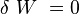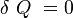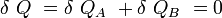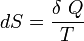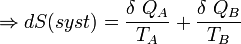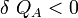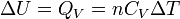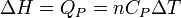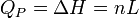Transfert thermique - Définition

Chaleur et thermodynamique

Évolution de deux corps en contact

Soient deux objets A et B indéformables dans un système parfaitement isolé thermiquement et mécaniquement, ayant les caractéristiques suivantes :

Objet A	Objet B
Volume VA	Volume VB
Température TA (TA > TB)	Température TB
Masse mA	Masse mB
Chaleur spécifique cpA	Chaleur spécifique cpB

Dans ce cas, le sens du transfert thermique est gouverné par la différence de température entre les deux corps. L’expérience montre que c’est le corps chaud qui cède de l’énergie au corps froid de façon à ce que, à l’équilibre, les températures des deux corps soient identiques.

Conformément au premier principe de la thermodynamique, nous pouvons écrire que l’énergie interne est égale à la somme de la chaleur et du travail :

• Les objets sont indéformables donc :

• Le système est isolé donc :

Si δQ_A et δQ_B sont respectivement les énergies thermiques élémentaires échangées entre l’objet A et l’objet B, faisant partie du système isolé.

D’où :

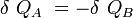
Le deuxième principe de la thermodynamique permet d’écrire la relation suivante liant les entropies des objets A et B :

, puisque le système est isolé.

par définition.

Nous pouvons écrire :

Si : T_A > T_B

Cela signifie que :

et donc que :

D’après la règle des signes, on conclut que l’objet A cède de la chaleur à l’objet B. L’objet le plus chaud cède donc de la chaleur à l’objet le plus froid.

Le premier principe et la chaleur

Le premier principe de la thermodynamique est un principe de conservation de l'énergie. Il introduit la fonction d'état énergie interne U .

Au cours d'une transformation d'un système thermodynamique fermé, entre deux états I et F la variation de l'énergie interne U(F) - U(I) est due à la somme :

• des travaux macroscopiques réalisés , en général le travail des forces de pression.
• des transferts d'énergies microscopiques ou chaleurs, .

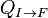
Ce qui se traduit par :

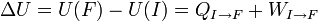
On en déduit donc une définition formelle de la chaleur le long d'un chemin bien défini allant de I à F :

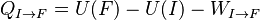
L'intégrale curviligne permettant le calcul du travail des forces de pression: , n'est pas indépendante du chemin suivi pour aller de I vers F car le travail n'est pas une fonction d'état.

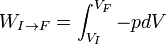
Il s'ensuit également que la chaleur n'est pas une fonction d'état et donc qu'elle dépend du chemin suivi. Notamment si la transformation permettant d'amener un corps d'un état I à un état F est réalisée de deux façons différentes, les chaleurs mises en jeu sont également a priori différentes.

Néanmoins dans certaines conditions expérimentales, la chaleur mise en jeu est égale à la variation d'une fonction d'état. C'est le cas pour une transformation d'un système fermé, effectuée à volume constant : la chaleur est égale à la variation d'énergie interne : ΔU = Q_V. Dans le cas d'une transformation à pression constante la chaleur est égale à la variation d'enthalpie : ΔH = Q_P . Ces deux propriétés sont mises à profit dans le domaine de la calorimétrie effectuée dans un calorimètre fonctionnant soit à pression constante soit à volume constant dans le cas d'une bombe calorimétrique.

Le second principe et la chaleur

Le second principe de la thermodynamique est un principe d'évolution. Il introduit la fonction d'état entropie qui est une mesure du désordre de la matière. La fonction entropie est définie à l'échelle macroscopique de telle sorte que sa variation au cours de la transformation réversible d'un système correspond au rapport de la quantité de chaleur échangée avec le milieu extérieur sur la température du système :

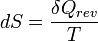
d'où :

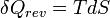
Et pour une transformation finie à température T constante, allant d'un état I à un état F d'équilibre :

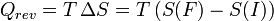
La chaleur est donc associée à une variation d'entropie. Or, plus il y a création d'entropie, plus la transformation est irréversible et plus le travail utile récupéré sera faible : ceci justifie le qualificatif donné à la chaleur d'être une dégradation qualitative de l'énergie (voir le deuxième principe de la thermodynamique).

Exemples de calcul de chaleur mise en jeu, au cours d'une transformation affectant un corps pur

Les grandeurs thermodynamiques associées à une quantité déterminée de corps pur (n constant) ne dépendent que de deux variables indépendantes.

Deux fonctions d'état introduites par le premier principe sont reliées à la chaleur sous certaines contraintes : V=cte ou P=cte.

• À volume constant, on choisit la fonction d'état énergie interne.

Car, à volume constant, la variation de la fonction énergie interne d'un corps pur est égale à la chaleur échangée avec le milieu extérieur.

Fonction d'état énergie interne: U(T,V)

Sa différentielle est égale à :

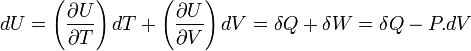
Si V = cte

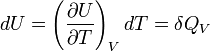
La grandeur est la capacité calorifique molaire à volume constant, appelée et qui s'exprime en J.K^-1.mol^-1.

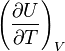
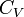
La chaleur mise en jeu pour une mole est donc égale à :

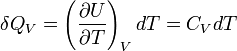
Pour n moles

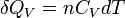
Enfin, pour une transformation isochore allant de l'état A défini par T_A à un état B défini par T_B

est fonction de T. Mais si l'intervalle de T n'est pas trop grand (quelques dizaines voire centaines de degrés), on peut la considérer en première approximation comme constante.

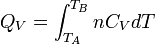
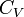
d'où:

• À pression constante, on choisit la fonction d'état enthalpie.

Car, à pression constante, la variation de la fonction enthalpie d'un corps pur est égale à la chaleur échangée avec le milieu extérieur.

Fonction d'état enthalpie: H(T,P)

Sa différentielle est égale:

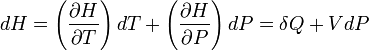
Si P = cte

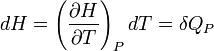
la grandeur est la capacité calorifique molaire à pression constante, appelée et qui s'exprime en J.K^-1.mol^-1.

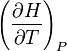
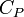
La chaleur mise en jeu pour une mole est donc égale à :

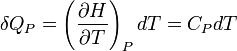
Pour n moles

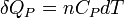
Enfin pour une transformation isobare allant de l'état A défini par T_A à un état B défini par T_B

est fonction de T. Mais si l'intervalle de T n'est pas trop grand (quelques dizaines voire centaines de degrés), on peut la considérer en première approximation comme constante.

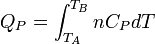
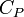
d'où :

• Cas du changement d'état physique.

Généralement, on considère le changement d'état physique effectué à l'air libre, c'est-à-dire à pression constante (pression atmosphérique). Tout le monde sait que la glace fond à 0 °C sous la pression atmosphérique et tant qu'il y a coexistence de la glace et de l'eau liquide, la température reste constante. Le changement d'état d'un corps pur s'effectue donc à P = Cte et T = Cte. La chaleur mise en jeu correspond donc à une variation d'enthalpie : ΔH puisque la pression est constante. On l'appelle encore chaleur latente molaire de changement d'état : L.