Tours de Hanoï - Définition
La liste des auteurs de cet article est disponible ici.
Applications
Les problèmes de la forme des Tours de Hanoï sont utilisés dans la recherche en psychologie de la résolution de problème. Ils peuvent aussi être employés comme épreuves lors d'une évaluation neuropsychologique des fonctions exécutives, en particulier sous la forme du test de la Tour de Londres.
Tours de Hanoï et Triangle de Pascal
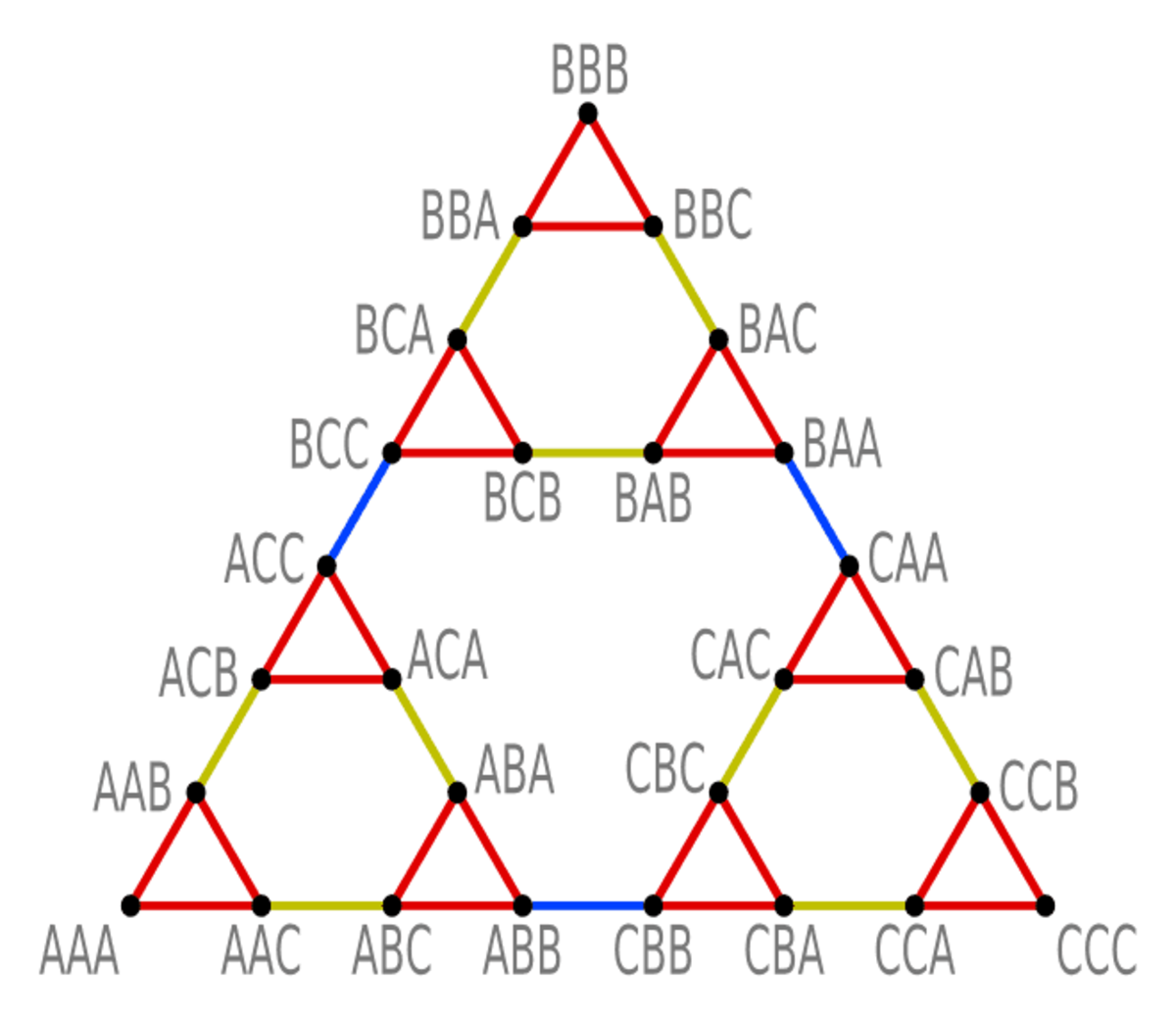
On peut représenter le jeu des Tours de Hanoï par un graphe abstrait, chaque sommet du graphe représentant une disposition possible des N disques sur les trois tours, une arête reliant deux sommets s'il existe un mouvement d'un disque permettant de passer d'une disposition, représentée par l'un des sommets, à l'autre. L'étiquetage des sommets est basé sur la position des disques dans la disposition qu'il représente : on lit de gauche à droite à quelle tour appartient chaque disque, en commençant par la position du plus grand disque.
Le diagramme montre l'arbre du jeu avec trois disques. La position initiale est située à l'un sommets du triangle, par exemple AAA, la position finale étant un autre sommet, BBB ou CCC. La couleur des arêtes indique le disque à déplacer : rouge pour le plus petit disque, jaune pour le disque intermédiaire, et bleu pour le grand disque.
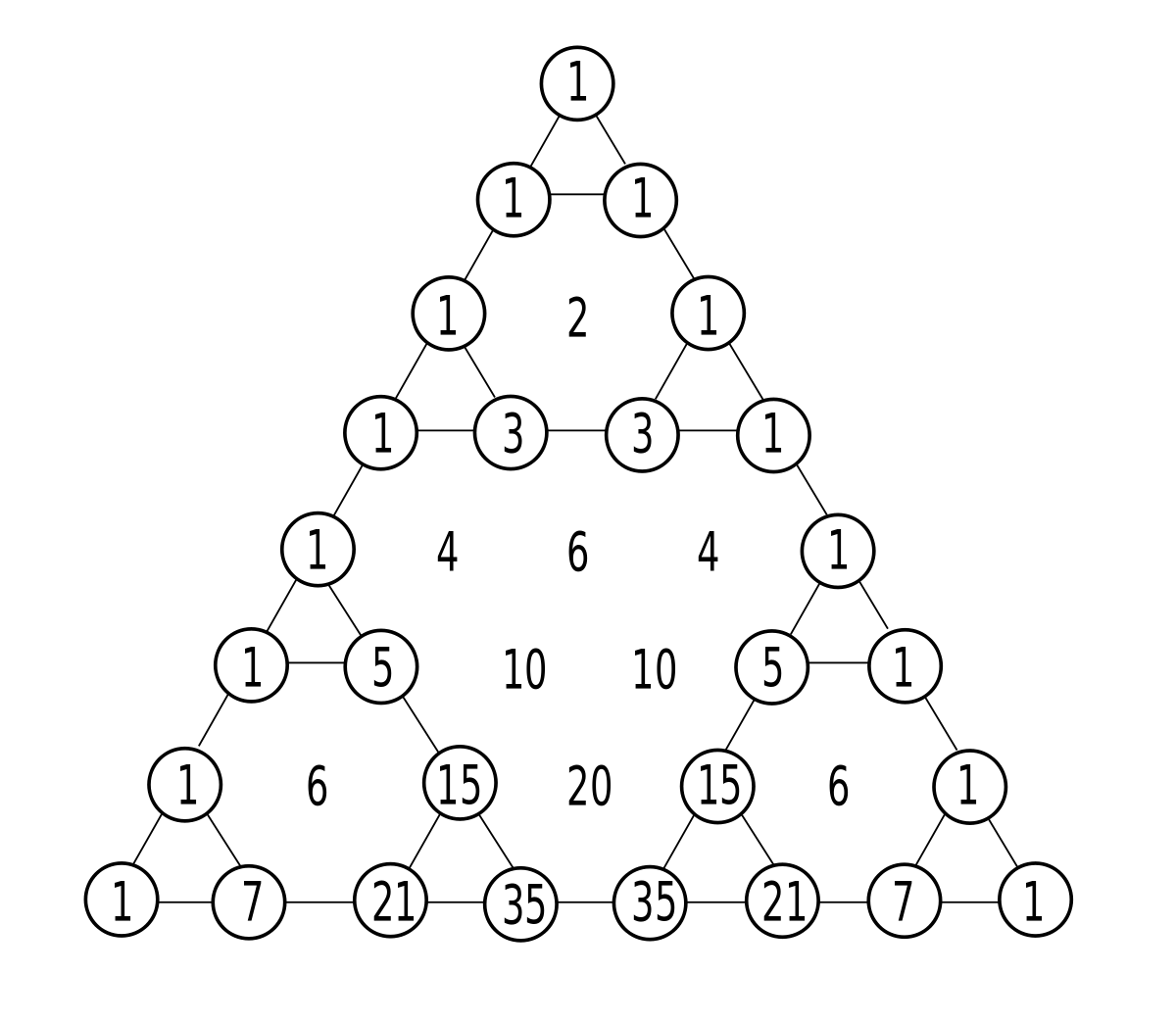
On montre que, pour tout N, le graphe des Tours de Hanoï à N disques est identique à celui obtenu à partir d'un Triangle de Pascal d'ordre 2N, où l'on relie par une arête les coefficients binomiaux impairs.

















































