Tours de Hanoï - Définition

Nombre de déplacements à effectuer

Il est facile de démontrer par récurrence que si N est le nombre de disques, il faut 2^N - 1 coups au minimum pour parvenir à ses fins, quantité qui augmente très rapidement avec N. En effet, soient a, b et c les trois emplacements des tours. Notons x_N le nombre de déplacements de disques nécessaires au déplacement d'une tour complète. Pour déplacer une tour de N disques de a vers c, on déplace la tour des N-1 premiers disques de a vers b, puis le disque N de a vers c, puis la tour des N-1 disques de b vers c. Le nombre de déplacements de disques vérifie donc la relation de récurrence :

ce qui donne bien

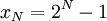
Codage des positions

Nous avons vu que, si p est impair, le p-ème coup consiste à déplacer le plus petit disque. Nous avons également vu que le déplacement du petit disque était cyclique. Par ailleurs, si p est pair, on vient de déplacer un autre disque, le plus petit disque ayant été déplacé au coup p-1 ; le disque que l'on vient de déplacer au coup p l'aurait été au coup ^p⁄₂ s'il n'y avait eu que N-1 disques.

Il résulte de ces préliminaires que, pour connaître la disposition des disques après le p-ème déplacement, il suffit de procéder comme suit.

Notons d(N,p) la position du plus petit disque après le p-ème coup (p impair), on a :

d(N,1) = d(N,7) = … = d(N,1+3k) = B si N est impair et = C si N est pair.

d(N,3) = d(N,9) = … = d(N,3k) = C si N est impair et = B si N est pair.

d(N,5) = d(N,11) = … = d(N,2+3k) = A.

Notons E(N,p) la suite des emplacements occupés par les N disques, du plus grand au plus petit, après p mouvements. On a alors, en notant par un point la concaténation entre deux listes de lettres :

Si p est pair, égal à 2m, E(N,2m) = E(N-1,m).d(N,2m-1)

Si p est impair, égal à 2m+1, E(N,2m+1) = E(N-1,m).d(N,2m+1)

Par exemple, la position au 12^e coup avec 4 disques est :

E(4,12) = E(3,6).d(4,11) = E(3,6).A

= E(2,3).d(3,5).A = E(2,3).AA

= E(1,1).d(2,3).AA = E(1,1).BAA

= BBAA

Résolution itérative

Il existe également une procédure itérative pour résoudre le problème des tours de Hanoï. Elle consiste à effectuer successivement les deux déplacements suivants, en désignant par A, B, C les trois tours :

• déplacer le plus petit disque d'un emplacement à l'emplacement suivant (de A vers B, de B vers C, de C vers A, par exemple)
• déplacer un autre disque

et à poursuivre itérativement ces deux déplacements jusqu'à ce que la tour complète soit déplacée, le dernier déplacement se limitant alors à celui du plus petit disque sur le sommet de la tour. L'action déplacer un autre disque est non ambigüe puisque, en dehors du plus petit disque, un seul mouvement d'un autre disque est possible.

Contrairement à la procédure récursive, la procédure itérative n'utilise aucune mémorisation de l'arbre des déplacements à effectuer et nécessite seulement de se souvenir si on doit déplacer le plus petit disque ou non, et dans quel sens sont effectués les déplacements du petit disque. Il permet également, à tout moment, de revenir à la situation de départ : il suffit pour cela d'inverser le sens dans lequel se déplace le plus petit disque. Par contre, les raisons pour lesquelles cet algorithme résout le problème sont moins apparentes que pour l'algorithme récursif.

Supposons que la tour soit initialement sur l'emplacement A, et qu'on veuille la déplacer sur l'emplacement B. Nous allons montrer par récurrence sur le nombre N de disques à déplacer que l'itération des deux mouvements décrits précédemment répond à la question, le sens dans lequel est déplacé le plus petit disque étant A → C → B → A → … → B si N est pair, et A → B → C → A → … → B si N est impair. En effet :

• Pour N = 1, il suffit de déplacer l'unique disque de A vers B. Supposons la propriété démontrée pour le déplacement de N-1 disques. Comme dans le cas récursif, on va déplacer la tour de N disques en déplaçant les N-1 disques supérieurs de A vers C, puis le grand disque de A vers B, puis les N-1 disques de C vers B.
• Si N est pair, alors N-1 est impair, et selon l'hypothèse de récurrence (en échangeant les rôles de B et C), lors du déplacement de la pile des N-1 disques supérieurs de A vers C, un déplacement sur deux est effectué par le plus petit disque dans l'ordre A → C → B → A → … → C. On déplace alors le grand disque de A vers B (déplacement qui succède au dernier déplacement du plus petit disque). Puis on déplace les N-1 disques de C vers B, un déplacement sur deux étant effectué par le plus petit disque, cette fois dans l'ordre C → B → A → C → … → B. Finalement, la suite des déplacements du petit disque aura bien été A → C → B → A → … → C → B → A → C → … → B, le plus petit disque étant déplacé une fois sur deux.
• On procédera à une vérification analogue si N est impair.