Torseur statique - Définition
La liste des auteurs de cet article est disponible ici.
Définition
Considérons une pièce 1 et une pièce 2 ayant un contact. Le torseur d'action de 2 sur 1 est noté
-
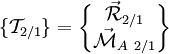
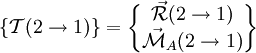
où la résultante
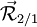
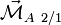
Ce torseur peut s'écrire en n'importe quel point. Le point A où l'on choisit de définir le moment est appelé « centre de réduction ».
Torseur d'action des liaisons parfaites
Au point de contact, une pièce ne peut transmettre un effort à une autre que si le mouvement relatif est bloqué. Chaque liaison mécanique bloque certaines translations et certaines rotations relatives. On peut donc connaître la forme qu'aura le torseur d'action réduit au point de contact si l'on connaît la liaison entre les pièces : le type de liaison « force » certaines composantes du torseur d'action à 0. On parle de torseur des actions mécaniques transmissibles (TAMT).
Ceci est résumé dans le tableau ci-dessous. Notez que l'emplacement des zéros dépend de l'orientation de la liaison par rapport aux axes du repère.
| Liaisons | Efforts possibles |
|---|---|
Ponctuelle

|
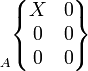
|
Linéaire rectiligne

|
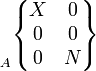
|
Linéaire annulaire

|
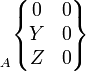
|
Rotule
|
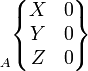
|
Pivot glissant
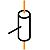
|
|
Appui plan
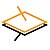
|
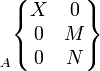
|
Pivot
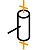
|
|
Glissière
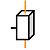
|
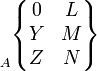
|
Hélicoïdale
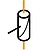
|
|
Rotule à doigt
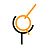
|
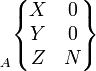
|
| Encastrement |
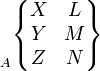
|
Cas particuliers
Un torseur dont la résultante est nulle est dit torseur couple.
Le torseur dont le moment et la résultante sont nuls est appelé le torseur nul {0}.
Lorsque le moment est perpendiculaire à la résultante, on dit que ce torseur est un glisseur :
-
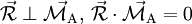
il existe un point tel que la réduction de ce torseur en ce point a un moment nul. Les torseurs représentant des forces seules sont des glisseurs, le point de réduction où le moment s'annule est le point d'application de la force.

















































