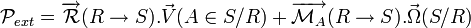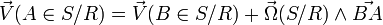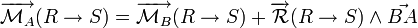Torseur - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définition - Propriétés des torseurs - Exemples - Principe fondamental de la dynamique - Torseurs couramment utilisés en mécanique - Autre acception - Exemple d'utilisation

Principe fondamental de la dynamique

En mécanique du solide, le principe fondamental de la dynamique (PFD) est généralisé pour décrire le mouvement de tous les points d'un solide (ou d'un ensemble de solides), à travers le concept des couples qui peuvent agir sur un solide mais n'ont pas de contrepartie en mécanique du point. Le PFD s'énonce ainsi :

il existe un repère galiléen, tel qu’à tout instant, le torseur dynamique du solide dans son mouvement par rapport à ce repère est égal au torseur des forces extérieures agissant sur le solide.

Dans le cas particulier du point matériel (en assimilant le solide à sa masse rapportée en son centre d'inertie), le PFD se réduit à l'égalité des résultantes de ces torseurs, soit le principe fondamental de la dynamique de translation.

Torseurs couramment utilisés en mécanique

Torseur statique

Torseur cinématique

Torseur cinétique

La résultante du torseur cinétique est constitué de l'impulsion, du système. Son moment est le moment cinétique.

Torseur dynamique

Autre acception

Soit G un groupe. Un G-torseur (traduction littérale de l'anglais G-torsor) désigne un ensemble sur lequel G agit de façon transitive (une seule orbite) et sans fixer aucun point. Cela équivaut à "oublier lequel des éléments de G est l'unité". Un G-torseur et le groupe G associé sont donc le même ensemble, mais muni de structures différentes.

L'espace affine en est un exemple pour le groupe des translations spatiales: additionner deux points n'a aucun sens, leur différence par contre est un élément du groupe additif des translations, c'est-à-dire un vecteur. De même, les notes de la gamme dodécaphonique (avec identification des octaves) forment un G-torseur pour le groupe additif Z_12 des entiers mod. 12, les jours de la semaine pour le groupe Z_7, etc. La droite réelle et le groupe additif des réels sont un autre exemple: l'énergie d'un système physique n'est définie que modulo une constante arbitraire, mais les variations d'énergie sont des éléments du groupe R.

La fibre d'un fibré principal est un G-torseur.

Puissance générale

De manière générale, tout solide en mouvement et subissant des efforts extérieurs peut être modélisé par 2 torseurs:

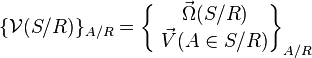
Le torseur cinématique décrivant le mouvement du solide : $\{\mathcal{V}(S/R) \}_{A/R} = \begin{Bmatrix} \ \vec \Omega (S/R) \\ \ \vec V (A \in S/R) \end{Bmatrix}_{A/R}$

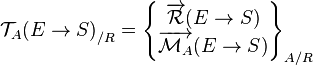
Le torseur des efforts extérieurs ou torseur statique (S: le solide, E: l'extérieur) : ${\mathcal{T} _A (E \to S) }_{/R} = \begin{Bmatrix} \overrightarrow{\mathcal{R}}(E \to S) \\ \overrightarrow{\mathcal{M}_A}(E \to S) \end{Bmatrix}_{A/R}$

Puissance extérieure ( $\mathcal{P}_{ext}$ )

Soit un ensemble de solides (notés $\mathcal{S}_i$ avec i un indice) qui constitue ce que l'on appelle un système (noté $S$ ). La puissance extérieure est la puissance de tous les efforts extérieures qui s'appliquent sur le système. On se place par rapport au référentiel $R$ qui est le référentiel de base c'est-à-dire le référentiel du laboratoire, considéré comme galiléen.

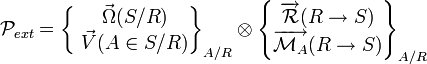
Pour calculer la puissance extérieure instantanée du système en mouvement subissant des efforts extérieurs, on calcule le comoment ( $\otimes$ ) des 2 torseurs : $\mathcal{P}_{ext} = \begin{Bmatrix} \ \vec \Omega (S/R) \\ \ \vec V (A \in S/R) \end{Bmatrix}_{A/R} \otimes \begin{Bmatrix} \overrightarrow{\mathcal{R}}(R \to S) \\ \overrightarrow{\mathcal{M}_A}(R \to S) \end{Bmatrix}_{A/R}$

Ce qui donne en fait la formule suivante :

$\mathcal{P}_{ext} = \overrightarrow{\mathcal{R}}(R \to S).\vec V (A \in S/R) + \overrightarrow{\mathcal{M}_A}(R \to S).\vec \Omega (S/R)$

Puissance intérieure ( $\mathcal{P}_{int}$ )
Les puissances intérieures ( $\mathcal{P}_{int}$ ) d'un système sont les puissances entre les divers solides. Il faut utiliser la même méthode de calcul c'est-à-dire effectuer un comoment des 2 torseurs. Seulement il faut faire très attention aux torseurs à utiliser. En effet, ce comoment s'effectue entre le torseur des efforts d'un solide sur un autre et le torseur distributeur des vitesses du solide en question par rapport à l'autre solide!! .

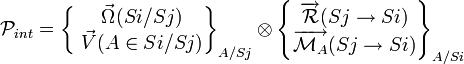
Ce qui donne : $\mathcal{P}_{int} = \begin{Bmatrix} \ \vec \Omega (Si/Sj) \\ \ \vec V (A \in Si/Sj) \end{Bmatrix}_{A/Sj} \otimes \begin{Bmatrix} \overrightarrow{\mathcal{R}}(Sj \to Si) \\ \overrightarrow{\mathcal{M}_A}(Sj \to Si) \end{Bmatrix}_{A/Si}$

Remarques :

C'est la formule générale. Si on considère un solide en translation ou si on considère un solide en rotation subissant un couple, on retombe sur les formules déjà précédemment énoncées.
La puissance instantanée calculée de cette manière ne dépend pas du point A du solide mais le comoment doit être calculé avec les 2 torseurs exprimés au même point
L'expression de ces 2 types de puissances nous amène au théorème de l'Énergie cinétique :

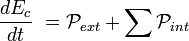
$\frac{dE_c}{dt}\ = \mathcal{P}_{ext} + \sum \mathcal{P}_{int}$

Démontrons que la puissance ne dépend pas du point du solide :

Formules de changement de point (la vitesse et le moment sont des vecteurs qui s'expriment en un point) :

$\vec V (A \in S/R) = \vec V (B \in S/R) + \vec \Omega (S/R) \land \vec {BA}$
$\overrightarrow{\mathcal{M}_A}(R \to S) = \overrightarrow{\mathcal{M}_B}(R \to S) + \overrightarrow{\mathcal{R}}(R \to S) \land \vec {BA}$

La puissance exprimée au point A est :
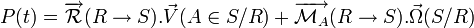
$P(t) = \overrightarrow{\mathcal{R}}(R \to S).\vec V (A \in S/R) + \overrightarrow{\mathcal{M}_A}(R \to S).\vec \Omega (S/R)$
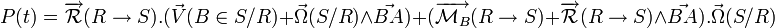
On utilise la formule de changement de point : $P(t) = \overrightarrow{\mathcal{R}}(R \to S).(\vec V (B \in S/R) + \vec \Omega (S/R) \land \vec {BA}) + (\overrightarrow{\mathcal{M}_B}(R \to S) + \overrightarrow{\mathcal{R}}(R \to S) \land \vec {BA}).\vec \Omega (S/R)$
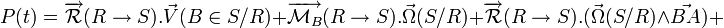
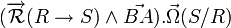
Puis on développe : $P(t) = \overrightarrow{\mathcal{R}}(R \to S).\vec V (B \in S/R) + \overrightarrow{\mathcal{M}_B}(R \to S).\vec \Omega (S/R) + \overrightarrow{\mathcal{R}}(R \to S).(\vec \Omega (S/R) \land \vec {BA}) +$ $(\overrightarrow{\mathcal{R}}(R \to S) \land \vec {BA}).\vec \Omega (S/R)$
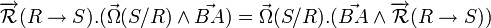
Or on sait que : $\overrightarrow{\mathcal{R}}(R \to S).(\vec \Omega (S/R) \land \vec {BA}) = \vec \Omega (S/R).(\vec {BA} \land \overrightarrow{\mathcal{R}}(R \to S))$ (permutation circulaire).
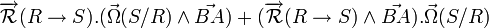
Donc le terme : $\overrightarrow{\mathcal{R}}(R \to S).(\vec \Omega (S/R) \land \vec {BA}) + (\overrightarrow{\mathcal{R}}(R \to S) \land \vec {BA}).\vec \Omega (S/R)$ est en fait nul.
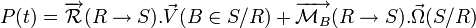
Finalement on tombe donc sur : $P(t) = \overrightarrow{\mathcal{R}}(R \to S).\vec V (B \in S/R) + \overrightarrow{\mathcal{M}_B}(R \to S).\vec \Omega (S/R)$
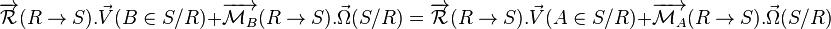
Autrement dit, pour tout point A et B du solide, on a l'égalité vectorielle suivante : $\overrightarrow{\mathcal{R}}(R \to S).\vec V (B \in S/R) + \overrightarrow{\mathcal{M}_B}(R \to S).\vec \Omega (S/R) = \overrightarrow{\mathcal{R}}(R \to S).\vec V (A \in S/R) + \overrightarrow{\mathcal{M}_A}(R \to S).\vec \Omega (S/R)$

Conclusion : on a donc bien démontré que la puissance ne dépend pas du point choisi.

Exemples

Exemple d'utilisation

- Introduction - Définition - Propriétés des torseurs - Exemples - Principe fondamental de la dynamique - Torseurs couramment utilisés en mécanique - Autre acception - Exemple d'utilisation

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

L'Univers comme jamais vu auparavant: les révélations du fond diffus cosmologique 🔭

C'est sérieux: de la bave pourrait révolutionner la conception de bioplastiques 🪱

Découverte: le trou noir central de notre galaxie pourrait anéantir la vie sur Terre 💥

Etude scientifique: ces aliments nous font vieillir 🍽️

Pourquoi notre visage est-il plus petit et délicat que celui des Néandertaliens ? 🤔

A 18 ans, il découvre 1,5 million d'objets célestes inconnus avec son algorithme d'IA 🌟

Que sont ces objets rouges et aplatis, qualifiés d'UFOs par les astronomes ? 🔭

Une méthode simple pour améliorer les performances en mathématiques 🧮

Que sont ces étranges éclairs rouges photographiés au-dessus de l'Himalaya ? ⚡

Nous descendons non pas d'un, mais d'au moins deux groupes anciens 🧬

Un nuage géant de 160 000 soleils découvert dans notre Voie lactée 🔭

Connaissez-vous le rat-kangourou musqué, ce marsupial à la démarche unique ? 🦘

Comment une poignée de traders a fait s'effondrer deux cryptomonnaies 📉

Première cartographie titanesque d'un cerveau, avec 500 millions de connexions neuronales 🧠

Cette double supernovae proche est inexorable, voici la date... qui va vous surprendre 💥

Un océan phosphorescent: comment s'explique ce phénomène rare et féerique ? 🌊

L'ELT pourrait-il découvrir une vie extraterrestre dès 2028 ? 🔭

Cet édulcorant tue les superbactéries résistantes 🍬

Les neutrinos, la clé de la gravité quantique ? 👀

En Italie, les éruptions explosives de ce volcan déjouent les pronostics 🌋

Que sont ces spaghettis au cœur de notre galaxie ? 🔭

Des scientifiques ont créé une "bombe intelligente" contre le cancer 🎯

Les nanoplastiques, l'amiante du 21ème siècle ? 🔬

Compétition cellulaire: des forces sculptent nos tissus 🛠️

Le climat en Europe et au États-Unis pourrait changer bien plus radicalement que supposé 🌍

Découverte: ce dinosaure avait des poches d'air dans les os 🦴

La vie sur Titan, si elle existe, ressemblerait à quoi ? 🪐

Magnétisme et biologie s'allient contre le cancer 🧲

WR 104: on en sait plus sur cette "étoile de la mort" qui menace la Terre ☄️

Découverte: des bactéries respiraient de l'oxygène 1 milliard d'années avant la Grande Oxydation 🫧

Découverte d'un nouveau type de vent solaire rapide ☀️

Les dinosaures n'étaient pas en déclin avant l'astéroïde 🦖

Ce robot-cheval est véritablement tout-terrain 🐎

Comment un mauvais sommeil peut endommager votre cerveau ? 🧠

Découverte de microbes cachés qui purifient l'eau sans que nous le sachions 💧

Bonne nouvelle pour les enfants de la Lune 🌙

Du CO2 détecté dans l'atmosphère d'une exoplanète proche 🔭

Le café et le thé impactent le cancer, mais dans quel sens ? ☕

Une IA révèle des bulles cosmiques dans notre galaxie 🫧

Lorsque l'alcool stimule ses phéromones sexuelles et rend plus séduisant 🍷

Page générée en 0.088 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise