Tolérance géométrique - Définition
La liste des auteurs de cet article est disponible ici.
Exemple : perpendicularité d'un alésage
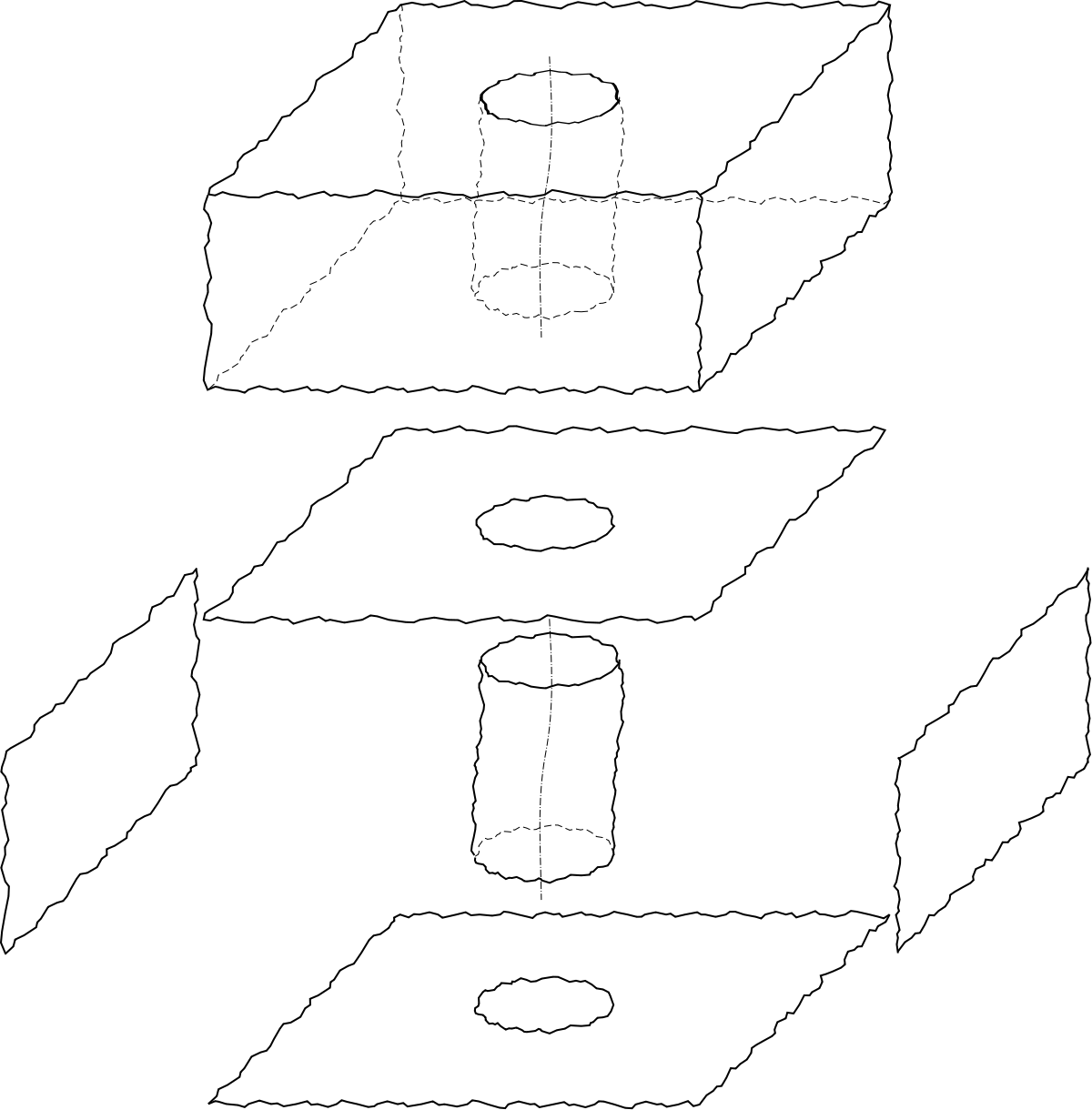
Développons l'exemple de la perpendicularité d'un alésage par rapport à une surface. La figure ci-contre montre
- une représentation en perspective de la pièce idéale avec la cotation de la perpendicularité ; A est le nom du plan, t est la tolérance (un nombre en millimètres, typiquement entre 0,01 et 1 mm) ;
- une représentation de la pièce réellement réalisée ; les défauts sont amplifiés (anamorphose).
Du modèle de peau à l'objet idéal
On considère la pièce réelle, et on en « extrait » la partie qui nous intéresse, ici l'alésage ; on dit que l'on partitionne la pièce. La surface de cette partie, surface non idéale, est appelée modèle de peau ou skin model. Puis, on détermine un objet idéal à partir de ce modèle de peau, ici, le cylindre parfait du plus grand diamètre inscrit dans l'alésage. D'un point de vue du contrôle, cela revient à essayer différentes piges — des cylindres calibrés — de diamètre croissant et à retenir la pige la plus grande entrant dans le trou, ou bien à utiliser un mandrin expansible (alésomètre).
Ce cylindre idéal est le cylindre associé à l'alésage ; il a un axe et une surface, on s'intéresse ici à son axe.
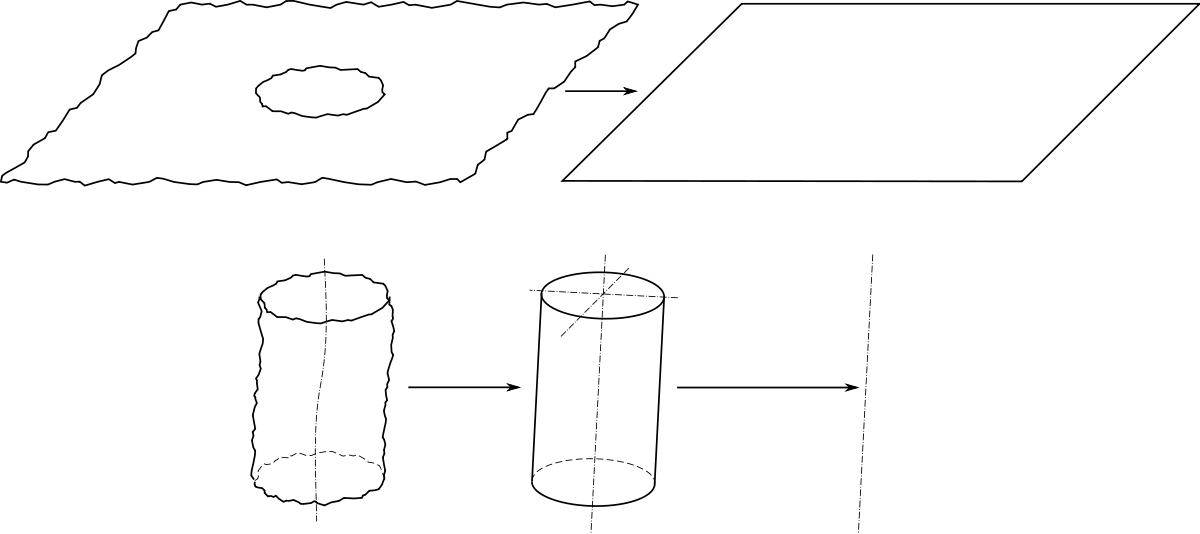
Puis, on isole la surface nominalement plane, et on prend le plan tangent ayant la direction moyenne du plan. D'un point de vue du contrôle, cela revient à poser la pièce sur un marbre ; d'un point de vue mathématique, on détermine le plan parfait minimisant l'écart quadratique par rapport à la surface réelle (méthode des moindres carrés, voir l'article Régression linéaire), et on le translate pour qu'il soit à l'extérieur de la matière. Ce plan idéal est le plan associé à la surface réelle.
Repère et zone de tolérance
Reste à définir les orientations acceptables de l'axe par rapport au plan. Pour cela, on prend la normale au plan, et on construit un cylindre ayant pour axe cette normale, et ayant pour diamètre la tolérance, indiquée en millimètres ; c'est la zone de tolérance (ZT). L'alésage est conforme si l'axe du cylindre parfait associé peut être placé entièrement dans cette zone de tolérance.
La perpendicularité est une affaire d'angle, on pourrait donc pu s'attendre à ce que l'on définisse une tolérance en degrés, la zone de tolérance aurait alors été un cône. Mais en cotation GPS, les tolérances sont toujours indiquées en millimètre, les zones de tolérances sont toujours des formes extrudées (ayant une section droite uniforme), à quelques exceptions près (tolérances de forme quelconque).
Les différentes tolérances
Tolérances de forme
Les tolérances de forme ne font appel à aucun repère ; les zones de tolérance ne sont ni contrainte en position, ni en orientation (principe d'indépendance) .
Il faut distinguer les tolérances de forme de la rugosité, voir l'article État de surface.
Ligne quelconque
Le cas général de la forme d'une ligne quelconque.

Surface quelconque
Le cas général de la forme d'une surface quelconque.

Rectitude
Le cas particulier de la rectitude.
Une ligne quelconque du plan suivant une direction donnée, doit être comprise entre deux droites parallèles distante de la valeur de la tolérance.
Circularité
Le cas particulier de la circularité.

Le profil (que l'on espère assez proche de la forme circulaire !) doit être compris entre deux cercles concentriques et coplanaires dont la différence des rayons est inférieure ou égale à la valeur de tolérance. La circonférence intérieure est la plus grande circonférence inscrite dans le profil tandis que la circonférence extérieure est la plus petite circonférence circonscrite dans le profil.
Planéité
Le cas particulier de la planéité.

On parlera de « surface plane », un « plan » étant un objet s'étendant à l'infini. Pour une surface réelle, on parle de « surface réputée plane » ou de « surface nominalement plane ».
La surface plane tolérancée doit être comprise entre deux plans parallèles distants de la valeur de la tolérance donnée.
Cylindricité
Le cas particulier de la cylindricité.
La surface tolerancée doit être comprise entre deux cylindres coaxiaux dont les rayons diffèrent de la valeur de la tolérance. Le cylindre extérieur est le plus petit cylindre circonscrit.
Tolérances d'orientation
Ligne quelconque
Le cas général de la forme d'une ligne quelconque.

Surface quelconque
Le cas général de la forme d'une surface quelconque.

Inclinaison
Le cas général de l'inclinaison.
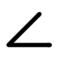
La surface tolérancée est comprise dans une zone de tolérance définie par deux plans parallèles distants de la valeur de la tolérance. La zone de tolérance est contrainte en orientation seulement.
Parallélisme
Le cas particulier du parallélisme.
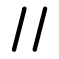
La surface tolérancée est comprise dans une zone de tolérance définie par deux droites parallèles distants de la valeur de la tolérance et parallèles au plan de référence. la zone de tolérance est contrainte en orientation seulement.
Perpendicularité
Le cas particulier de la perpendicularité.
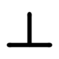
La surface doit être comprise entre deux plans perpendiculaires au plan de référence et distants de la valeur de la tolérance.
Tolérances de position
Ligne quelconque
Le cas général de la forme d'une ligne quelconque.

Surface quelconque
Le cas général de la forme d'une surface quelconque.

Spécification de localisation
Le cas général de la localisation.

Coaxialité/concentricité
Le cas particulier de la coaxialité/concentricité.

Symétrie
Le cas particulier de la symétrie.
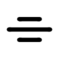
Tolérances de battement
Battement simple
Le cas général du battement simple.

- Battement simple axial
La zone de tolérance est limitée pour chaque position radiale, par deux circonférences distantes de t situées sur le cylindre de mesurage dont l'axe coïncide avec l'axe de référence.
- Battement simple radial
La zone de tolérance est limitée dans chaque plan de mesurage perpendiculaire à l'axe par deux cercles concentriques distants de t dont le centre coïncide avec l'axe de référence.
- Battement simple oblique
La zone de tolérance est limitée sur chaque cone de mesurage par deux circonférences distantes de t. Chaque cone de mesurage a ses génératrices dans la direction spécifiée et son axe coïncide avec l'axe de référence.
Battement total
Le cas général du battement total.

Exceptions au principe d'indépendance
Exigence de l'enveloppe
L'exigence d'enveloppe consiste à imposer que l'objet tolérancé soit compris dans une enveloppe parfaite au maximum de la tolérance dimensionnelle. Elle s'indique par un E entouré Ⓔ placé après la valeur de la cote dimensionnelle.
Exigence du maximum de matière
L'exigence du maximum de matière revient à considérer la montabilité d'un système. L'idée est qu'un défaut peut compenser un autre défaut, ce qui permet d'accepter des pièces qui, si l'on considérait les défaut indépendamment, auraient été rebutées.
Considérons par exemple un système pièce mâle/pièce femelle, la pièce mâle comparant deux protubérances cylindriques et la pièce femelle deux alésages. Pour que le système soit montable, il faut pour chaque pièce
- que les cylindres aient un diamètre correct ;
- que la distance séparant les diamètres soit correcte.
On a donc une tolérance de localisation d'un cylindre par rapport à l'autre, et une tolérance dimensionnelle sur le diamètre.
Mais si un cylindre est plus petit, il y a plus de jeu, ce qui permet d'avoir une erreur plus grande sur la localisation. Mais alors la cote géométrique n'est plus indépendante de la cote dimensionnelle.
On travaille alors avec une zone de tolérance unique qui concerne le cylindre en entier : tant que le cylindre est compris en entier dans la ZT, peu importe son diamètre exact ou sa localisation exacte. Cette ZT est obtenue en considérant le maximum de matière, c'est-à-dire la protubérance de plus grand diamètre ou l'alésage de plus petit diamètre.
L'exigence du maximum de matière s'indique par un M entouré Ⓜ placé après la cote dimensionnelle.
Exigence du minimum de matière
L'exigence du minimum de matière est indiquée par un L entouré Ⓛ placé après l'intervalle de tolérance, au sein d'un cadre de tolérancement géométrique. Cette exigence permet de définir l'intervalle de tolérance maximal admis, lorsque les pièces sont les plus légères. Ce calcul se fait, lorsque l'on veut vérifier des conditions de résistance. Cette exigence, comme le maximum de matière permet de rendre dépendant l'intervalle de tolérance en fonction de l'évolution d'une cote dimensionnelle. Ce type d'écriture sur les plans permet d'accepter davantage de pièces conformes qui répondent aux exigences de résistance.