Théorie des figures d'équilibre - Définition

Introduction

La théorie des figures d'équilibre considérée ici résulte de nombreuses études traitant du problème de la forme d'équilibre de la Terre, en supposant que celle-ci soit causée par la seule force de pesanteur, à l'exclusion de forces de cohésion internes ou de forces électriques et magnétiques. La théorie présentée repose entièrement sur la notion de surface de niveau, et requiert donc l'existence d'un potentiel de pesanteur à l'intérieur du corps que l'on étudie. Cela exclut la présence d'une rotation différentielle sauf si celle-ci correspond à une rotation différentielle en couches cylindriques coaxiales.
Bien que ce problème soit vieux de plus de trois siècles (cf Modèle ellipsoïdal de la Terre), il n'en continue pas moins à être un problème actuel qui possède des applications intéressantes en géodésie et en géophysique. Il est fermement enraciné dans la théorie générale des figures de corps cosmiques en rotation, qui constitue elle-même un domaine de recherche active en astrophysique et en physique planétaire. Toutefois, pour des corps cosmiques en rotation lente — comme c'est le cas de la Terre — et pour autant que nous puissions admettre qu'il y a équilibre hydrostatique, la théorie des figures semble avoir atteint un niveau de finition acceptable. L'étude de la figure hydrostatique de la Terre n'a pas seulement exercée une profonde influence sur la naissance et le développement subséquent de la géodésie physique et de la géophysique, mais elle a aussi grandement contribué aux fondations de la physique de Newton, de l'hydrostatique, de la mécanique analytique, de l'analyse mathématique et de la physique mathématique pendant les XVIII^e et XIX^e siècles, et se trouve associée à la plupart des noms des mathématiciens et physiciens les plus distingués de cette époque.

Équations fondamentales

Pour étudier la figure d'équilibre hydrostatique de la Terre, on se place dans le cadre général de la mécanique des milieux continus. Les équations de base d'un continuum sont, en formulation eulérienne :

• l'équation de continuité, qui exprime la conservation de la masse :

  ,

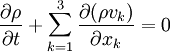• l'équation de mouvement, qui exprime la conservation de la quantité de mouvement, ou impusion :

  .

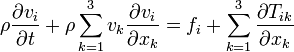Dans ces équations, ρ(x, x, x) désigne la densité en un point spatial P repéré par ses coordonnées cartésiennes (x, x, x)), (v, v, v) le champ de vitesses au même point, (f, f, f) le champ de force volumique et T, avec i ,k = 1, 2, 3, le tenseur des contraintes en P.

Dans les circonstances habituelles, que nous supposerons réalisées ici

• l'équation de rotation qui exprime la conservation de la quantité de rotation, ou moment cinétique, implique que le tenseur des tensions est symétrique

  T_ik = T_ki,

et se réduit donc à six composantes indépendantes au lieu de neuf : T, T, T, T = T, T = T, T = T.

Rotateur permanent

Définition d'un rotateur permanent

On peut simplifier le problème encore davantage en supposant que la figure de'équilibre constitue un rotateur permanent. On définit un corps en rotation permanente comme suit :

• il est isolé dans l'espace et tourne autour d'un axe fixe ;
• son mouvement est stationnaire dans un système d'inertie, et la densité de chaque point massique individuel reste constante au cours du mouvement ;
• on peut négliger les effets dissipatifs, notamment les frictions ;
• aucune force électromagnétique n'agit sur le corps.

Champ de vitesse d'un rotateur permanent

Constatons que l'on n'a pas encore spécifié la vitesse angulaire ω. Admettons maintenant que le corps tourne autour de l'axe (O x) et prenons l'origine O du système d'axes au centre de masse du corps. Considérons des coordonnées cylindriques (h, λ, z) définies en termes des coordonnées cartésiennes (x, x, x) par la loi de transformation :

.

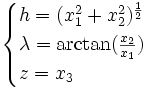Ainsi, dans un système d'inertie, les composantes de la vitesse prennent la forme

.

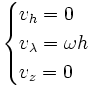Équation de continuité pour un rotateur permanent

Comme la densité d'un point massique appartenant à un rotateur permanent ne varie pas le long de sa trajectoire, nous avons

.

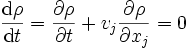L'équation de continuité implique donc que le mouvement est indivergentiel, c'est-à-dire

.

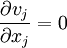Symétrie du champ de vitesse d'un rotateur permanent

En coordonnées cylindriques, cette équation devient

,

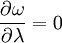ce qui implique qu'une rotation permanente est caractérisée par un champ de vitesse qui ne dépend pas de la variable λ, soit

ω = ω(h,z) .

Un cas particulier d'un rotateur permanent est un rotateur rigide, pour lequel la vitesse angulaire est constante :

ω = Constant.

Le corps concerné tourne alors en bloc sur lui-même : on dit que la figure d'équilibre correspondante est en équilibre relatif.

Or, l'hypothèse d'une rotation permanente ne requiert pas seulement que dρ/dt = 0, mais aussi que ∂ρ/∂t = 0, d'où l'on tire au moyen de l'équation de continuité que

.

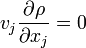Cette dernière relation montre que pour une rotation permanente les lignes de courant sont orthogonales au gradient de densité local. Dans le système de coordonnées cylindriques que nous avons adopté, cette relation s'écrit

.

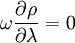Symétrie de la distribution de masse d'un rotateur permanent

En supposant que le corps tourne effectivement (ω ≠ 0) comme un rotateur permanent par rapport à un référentiel d'inertie, nous trouvons donc que

ρ = ρ(h,z).

On en déduit que la distribution de densité dans un rotateur permanent possède une symétrie axiale, et la même conclusion s'impose (voir ci-dessus) pour le champ de vitesse angulaire. Ainsi, ce champ ω = ω(h, z) ne possède pas de tourbillon dans le plan (O x x), donc

.

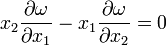Équation de mouvement d'un rotateur permanent

En termes de coordonnées cartésiennes, le champ de vitesse peut donc s'écrire

.

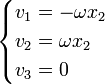En vertu des relations ∂v/∂x = 0 et v ∂ρ/∂x = 0,, la quantité ∂(ρ v v) / ∂ devient simplement ρ v ∂v / ∂x. Dès lors, l'équation de mouvement prend la forme particulière

.

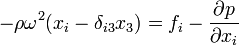Potentiel gravifique d'un rotateur permanent

Selon la définition d'un rotateur permanent énoncée plus haut, il est évident que le champ de force volumique f est simplement le champ de force engendré par l'autoattraction gravitationnelle, c'est-à-dire

f_i = ρg_i.

Il est bien connu que la force gravifique spécifique g en un point P est fournie par l'expression

,

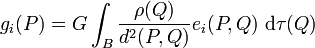où d(P, Q) représente la distance entre le point attiré P et un quelconque point attirant Q du corps B. La quantité e désigne la i^e composante d'un vecteur unitaire porté par le segment de droite qui joint P à Q, et orienté de P à Q. L'élément de volume en Q est dénoté par dτ(Q). On sait de même que la force volumique g dérive en chaque point de l'espace d'une fonction scalaire V, appelé potentiel gravitationnel. Ainsi,

.

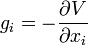Nous définissons ici ce potentiel V, en accord avec la convention généralement adoptée par les physiciens, comme l'énergie potentielle par unité de masse d'un élément matériel situé au point P. Cette énergie potentielle résulte de l'interaction gravitationnelle de l'élément matériel en P avec tous les autres éléments matériels composant le corps B, de sorte que

.

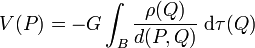Selon cette définition, le potentiel gravifique est toujours négatif, et correspond physiquement à une énergie de liaison. Il faut remarquer que les astronomes et les géodésiens, et aussi de nombreux géophysiciens, adoptent une définition différente pour le potentiel gravifique, à savoir ils l'assimilent au travail qu'un élément matériel de masse unitaire accomplit dans le champ de force gravifique g en passant d'un point situé à l'infini au point P. Ce travail représente l'énergie potentielle par unité de masse changée de signe, et est donc positif. La convention des physiciens adoptée ici possède l'avantage, en retenant la correspondance directe entre potentiel et énergie potentielle, de faire en sorte qu'un point massique tend toujours à mouvoir vers des régions où le potentiel est plus bas. La constante G ci-dessus est la constante de gravitation.