Théorie des équations (histoire des sciences) - Définition

Introduction

Évariste Galois offre une condition nécessaire et suffisante à la résolution d'une équation polynomiale par l’algèbre. Il répond ainsi à une question centrale de la théorie, ouverte depuis des millénaires. Sa méthode fournit des résultats novateurs, à l’origine de nouvelles branches de l’algèbre, qui dépassent le cadre de la théorie des équations.

La théorie des équations est un ensemble de travaux ayant pour objectif premier la résolution d’équations polynomiales ou équivalentes. Une telle équation s’écrit de la manière suivante :

où X désigne l’inconnue.

La « théorie des équations » est une expression utilisée en histoire des sciences.

L’étude de ce type de questions remonte aux premiers textes mathématiques connus. Une première approche permet de résoudre l’équation dans le cas où le degré du polynôme est strictement plus petit que cinq. C'est durant la Renaissance et avec l'étude des équations cubiques que de nouveaux nombres sont utilisés. Ils sont qualifiés initialement d’imaginaires puis de nombres complexes. Ce n'est que plus tard que ceux-ci interviennent comme solutions d’équations de degré deux.

À partir de l'époque moderne, le polynôme est aussi considéré comme une fonction. Cette approche offre des méthodes pour déterminer le nombre de racines réelles, pour localiser les racines (c’est-à-dire trouver des régions où elles se trouvent) et pour fournir des méthodes d’approximations aussi précises que souhaité. L’un de ses achèvements est le théorème de d'Alembert-Gauss, qui indique qu’une fonction polynomiale non constante admet au moins une racine dans les nombres complexes.

Un point de vue du XIX^e siècle consiste à étudier le plus petit ensemble de nombres, stable pour les quatre opérations et qui contienne à la fois coefficients et racines d'une équation donnée. Cette approche entre dans la théorie dite de Galois. Elle offre une condition nécessaire et suffisante pour savoir si une équation polynomiale se résout par les techniques décrites par la première approche, dans le cas contraire l’on doit se limiter à des approximations issues de l’analyse. Jusqu’au XIX^e siècle, la théorie des équations se confond avec l’algèbre. Puis, à la suite de la théorie de Galois principalement, l’algèbre s’élargit pour prendre en compte de nouvelles questions. Cette théorie est à l’origine de vastes domaines mathématiques, comme la théorie des groupes, celle des anneaux ou encore la géométrie algébrique.

Remarque : Quand on ne précise pas, le terme de théorie des équations désigne généralement les équations polynomiales. En revanche, il existe de nombreuses équations qui, sans être algébriques, font néanmoins l’objet d’une théorie. L’usage veut alors que l’on précise la nature de l’équation, comme dans l’expression théorie des équations différentielles. Il n’existe pas de théorie unique s’appliquant à tout type d’équations, elles forment pour cela un ensemble trop disparate.

Origines

Avant la théorie

Le livre Arithmetica de Diophante est le premier à décrire l'inconnue au sens mathématique du terme.

Aussi loin que remontent les textes connus en mathématiques, on y trouve des questions qui s'expriment, en langage contemporain, sous forme d’équations algébriques. On lit, dans un papyrus de l’Égypte ancienne : « Quand le scribe te dit de quoi 10 est les 2/3 et le 1/10 ? » ce qui se traduit par 2/3x + 1/10x = 10. Des problèmes du second degré sont particulièrement étudiés par les Babyloniens. Leur langage est géométrique, la valeur recherchée, notée ici x, est appelée coté et x² carré, mais leur formulation est souvent purement algébrique. On peut lire, sur une tablette d’argile : « J’ai additionné 7 fois le côté de mon carré et 11 fois la surface : 6 15 », pour décrire (en numérotation sexagésimale utilisée par les Babyloniens) l’équation 11x² + 7x = 6x60 +  15= 375. Le sens géométrique de la somme d’une aire et d’une longueur est ambiguë, cependant aucun commentaire n’étaye une interprétation purement algébrique de la question (des nombres multipliés et additionnés). Aucun outil algébrique n’est développé, il n’existe pas d'inconnue que l’on peut déterminer à l’aide d'une méthode calculatoire. Les Égyptiens résolvent l’équation du premier degré par essais successifs, à l’aide de la méthode de la fausse position et les Babyloniens disposent d’algorithmes sans autre justification qu'empirique, c’est-à-dire qu’à la fin la valeur trouvée est bien la solution recherchée.

La première étape qui approche de l’ébauche d’une véritable théorie demande plus de deux millénaires. Elle est franchie indépendamment par trois cultures mathématiques : la Grèce, la civilisation arabe et celle des Indes. Diophante, un mathématicien du III^e siècle, formalise l'arithme, une lettre qu’il définit par : « Le nombre qui possède une quantité indéterminée d’unités s’appelle l’arithme, et sa marque distinctive est σ. » L’arithme s’additionne et se multiplie : « l’inverse de l’arithme multiplié par le bicarré de l’arithme donne le cube de l’arithme. » ce qui signifie en langage moderne que x divise x⁴ et que le résultat est égal à x³. Cette démarche permet une véritable formulation mathématique de l’équation et surtout, un mode de résolution. Avant que Diophante ne soit traduit en arabe, Al-Khawarizmi, un mathématicien d’origine perse, développe au VIII^e siècle une idée analogue. Son inconnue s’appelle le say’. Une fois encore, le nouveau formalisme offre un moyen de résolution de l’équation. R. Rashed indique : « [Avec Al-Khwarizmi] la notion de base c’est la notion d’équation, qui peut couvrir une classe infinie de problèmes, géométriques ou arithmétiques : l’unité n’est plus l’objet mais l’opération même. » La même idée est encore présente chez le mathématicien indien Bhāskara II dans son texte intitulé Bījagaṇita.

Les différentes méthodes de résolution des problèmes des premier et second degrés, avec et sans le formalisme de l’équation, sont présentées dans l’article détaillé.

Algèbre arabe

Les polynômes d’al-Samaw'al représentés par un tableau préfigurent une conception purement abstraite de l’algèbre.

Le mathématicien Al-Khawarizmi est souvent considéré comme fondateur de la branche des mathématiques appelée algèbre. En termes d’étymologie, le titre de son traité sur les équations : Kitâb al-jabr wa al-muqâbala utilise le terme al-jabr, devenu algèbre. En arabe, al-jabr vise « à transformer une soustraction dans un membre en une addition dans l’autre membre » dans l’objectif d’obtenir uniquement des coefficients positifs. Par exemple : 2x² + 100 - 20x = 58 devient en suivant ce procédé : 2x² + 100 = 58 + 20x. A. Dahan-Dalmedico et J. Peiffer précisent que le travail d’Al-Khawarizmi est : « l’acte de naissance d’une théorie des équations quadratiques, dans l’ensemble des nombres positifs (presque toujours rationnels), théorie qui comporte encore quelques lacunes ». Ce n’est pas uniquement l’étymologie qui justifie cette attribution à Al-Khawarizmi : en effet, celui-ci s’intéresse à toutes les équations du second degré, tandis que Diophante ne cherche à résoudre que quelques cas particuliers, à solutions entières ou rationnelles. Al-Khawarizmi a une démarche plus systématique : l’objet de son traité est d’offrir une méthode permettant de trouver à coup sûr, s'il en existe, une solution de l’équation.

Les progrès sur la théorie des équations ne s’arrêtent pas à Al-Khawarizmi. Il est à l’origine d’une école mathématique qui se développe sur plusieurs siècles. Son disciple Abu Kamil dissipe une première appréhension. À l’origine, les équations étudiées sont presque toujours à coefficients rationnels, Abu Kamil généralise l’étude aux coefficients irrationnels. La conception initiale du nombre chez les Arabes est héritée des Grecs et se limite aux fractions. Les grandeurs incommensurables, qui correspondent à nos irrationnels, sont des proportions entre longueurs, mais ne possèdent pas le statut de nombre. Al-Khawarizmi les appelle gidr asamm, qui signifie racine muette ou aveugle. Deux siècles plus tard, pour les mathématiciens comme Omar Khayyam, les fractions ou les proportions incommensurables sont traitées dans les calculs de la même manière, les deux concepts sont appelés al-adad, qui signifie nombre (les rationnels sont désignés par le terme al-adad al muntiqa et les irrationnels par al-adad al-summa), la différence n’étant plus que philosophique.

Des outils spécifiques sont développés pour permettre le calcul plus aisé des multiplications de polynômes. Al-Samaw'al les note sous la forme d'un tableau préfigurant une représentation proche du concept moderne de polynôme formel.

Géométrie au service de l’algèbre

Les gnomons et la géométrie d’Euclide sont le moteur de la résolution des équations algébriques pendant plusieurs siècles.

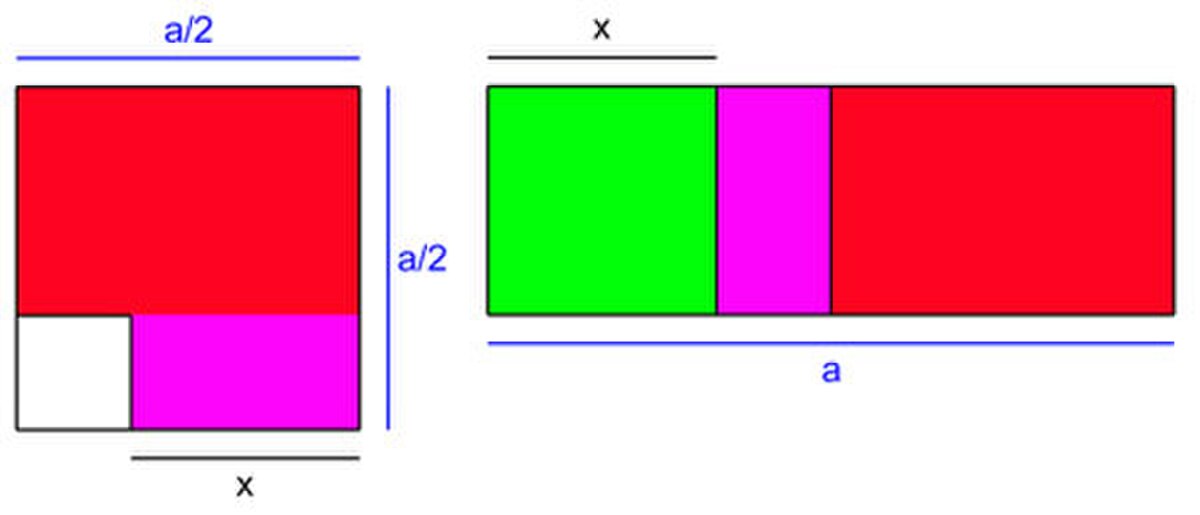
La géométrie, et particulièrement celle des Éléments d'Euclide, joue un rôle fondamental dans cette algèbre naissante. Dans le cas d’une équation du second degré et après division par le coefficient du monôme dominant, le monôme du second degré peut être vu comme l’aire d’un carré dont le côté est l’inconnue que l’on recherche. Dans le cas de l’équation du premier degré, on interprète le terme du premier degré comme l’aire d’un rectangle dont les dimensions sont l’inconnue et le coefficient du monôme ; la constante est interprétée comme l’aire d’un carré parfaitement déterminé. Cette approche permet déjà à Euclide de résoudre des problèmes des premier et second degrés. L’angle d’analyse des Arabes est différent puisqu’ils cherchent à résoudre une équation, dans ce cas particulier, du second degré. Cependant le cœur de la démonstration est le même : une analyse d’une configuration géométrique, construite sur la base d’un gnomon. De manière méthodique, l’étude du gnomon permet d’établir les trois identités remarquables source de résolution des équations du second degré.

L’approche utilisée pour étendre la théorie naissante des équations à l’équation cubique est tout aussi géométrique, mais cette fois avec des outils un peu différents. Al-Khayyām remarque qu’il est possible d’interpréter la racine de l’équation cubique comme l’abscisse de l’intersection d’un cercle et d’une parabole, ce qui montre déjà l’usage de ce que l’on appellera plus tard un repère cartésien et permet de remarquer l’existence possible de plusieurs solutions. Deux siècles plus tard, profitant des progrès tant algébriques que géométriques, Nasir ad-Din at-Tusi développe plusieurs outils dans le cadre de l’équation cubique. Le discriminant lui permet de connaître l’existence de racines positives dans certaines situations, la dérivation formelle lui permet de localiser les racines et une méthode numérique, variante de celle maintenant dite de Ruffini-Horner, permet d'approcher la racine avec la précision souhaitée.

Les méthodes mathématiques utilisées, ainsi que cette branche de l'histoire des mathématiques, sont développées dans l’article détaillé.

Diffusion en Europe

Girolamo Cardano généralise la formule de Tartaglia en lui adjoignant des nombres imaginaires pour résoudre des cas qualifiés alors d’irréductibles.

À travers les textes de Fibonacci ou encore de Luca Pacioli, l’Italie a accès, au début du XVI^e siècle, à l’essentiel du savoir arabe. Les mathématiciens d’alors se passionnent pour l’algèbre et, surtout, pour un problème laissé ouvert : trouver une méthode générale et exacte de résolution de l’équation cubique. Par exacte, on entend une forme différente d’une suite qui converge vers la racine. Ces mathématiciens recherchent une expression analogue à celle d’Al-Khawarizmi pour le second degré qui, à l’aide de racines carrées ou cubiques, donnerait la solution.

L’âpre compétition qui règne entre les différents mathématiciens stimule les candidats et pousse à l’émergence d’idées nouvelles. Scipione del Ferro trouve comme formule de résolution de l’équation X³ + aX = b :

A. Dahan-Dalmedico et J. Peiffer précisent : « Elle devait [...] provoquer de grands progrès dans la théorie des équations [...] ». La formule avait à l’époque de quoi susciter l’étonnement. Un calcul algébrique est encore justifié par un support géométrique. Un nombre tire sa justification d’une longueur, d’une aire ou d’un volume. Le signe - n’a de sens que si une longueur est soustraite à une plus grande. Dans la solution que propose del Ferro, on retranche une longueur à une autre longueur plus petite. À cette époque, l’enjeu est de relever des défis, c’est-à-dire de résoudre des équations particulières, la rigueur de la méthode importe peu, tant qu’il est finalement possible de vérifier le résultat en remplaçant x dans l’équation par la solution présumée.

Une question reste ouverte : comment résoudre l’équation X³ + a = bX, si 4b³ > 27a² ? Cette fois-ci, la méthode semble impraticable car la grandeur négative qui apparaît devrait correspondre à la surface d’un carré (au sens géométrique du terme). Tartaglia, un des spécialistes de l’époque en la matière, qualifie l’équation d’irréductible. C’est finalement Cardano qui trouve la solution : il suffit de ne pas arrêter les calculs. Ces étranges termes finissent par disparaître ; par exemple en appliquant des identités remarquables comme :

Une nouvelle étape est franchie. Si la signification précise de l’expression √-1 reste mystérieuse, l’idée de faire appel à un ensemble de nombres plus grand pour résoudre une question en théorie des équations est découverte. Un élève de Cardano, Ludovico Ferrari résout l’équation quartique, en 1540. Bombelli propose un formalisme autorisant l’existence de nombres négatifs et imaginaires. Son influence, attestée par les commentaires de Stévin ou la correspondance entre Leibnitz et Huygens, est durable.

L’article Méthode de Cardan présente la solution, en termes contemporains, de l’équation cubique, et celui intitulé Méthode de Ferrari celle du quatrième degré.