Théorie des ensembles - Définition

Les axiomes de la théorie ZF

Les systèmes axiomatiques pour la théorie des ensembles, ZF, Théorie des classes, Théorie des types sont équivalents au moins au sens où ils permettent tous de représenter l'essentiel des mathématiques. Parmi eux ZF est le plus courant et c'est pourquoi on en fait une description informelle ici.

La théorie qui se base sur les axiomes originaux de Zermelo est appelée théorie de Zermelo ou théorie Z. Si on la complète par l'axiome de remplacement de Fraenkel, on obtient la théorie de Zermelo-Fraenkel, ou plus simplement la théorie ZF, bien que la forme finale des axiomes soit due à Skolem. Lorsqu'on lui adjoint l'axiome du choix on obtient alors la théorie ZFC (« C » pour « choix »).

Un aspect important de la théorie ZF est que tous les objets dont elle traite sont des ensembles et ne peuvent être que des ensembles. En particulier, chaque élément d'un ensemble est lui-même un ensemble. D'autres objets mathématiques familiers, tels que les nombres, doivent donc par conséquent être définis en termes d'ensembles.

Strictement parlant, les axiomes de ZF sont simplement des énoncés du calcul des prédicats du premier ordre égalitaire dans un langage ayant un seul symbole primitif pour l'appartenance (relation binaire). Ce qui suit doit donc seulement être perçu comme une tentative d'exprimer en français la signification attendue de ces axiomes. De plus, l'axiome de séparation (ou compréhension) et l'axiome de remplacement sont en fait des schémas infinis d'axiomes.

1. Axiome d'extensionnalité : Si deux ensembles ont les mêmes éléments, alors ils sont égaux.
2. Axiome de l'ensemble vide : Il existe un ensemble sans élément. On le note (ou plus rarement {}). Cet axiome ne fait pas à proprement parler partie de l'axiomatisation de ZF, du moins dans sa version actuelle, formalisée en calcul des prédicats du premier ordre. On peut le déduire d'une propriété générique du calcul des prédicats, qui est qu'un modèle d'une théorie est non vide. Dans le cas de la théorie des ensembles, cela revient à dire qu'il existe au moins un ensemble, et cette propriété ne nécessite pas d'axiome spécifique : elle se démontre en logique pure. On en déduit par le schéma d'axiomes de compréhension l'existence de l'ensemble vide. On trouve cependant cet axiome dans des variantes de la théorie des ensembles, ou dans des présentations plus anciennes ou semi-formelles de la théorie ZF comme celle de Paul Halmos.
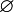
3. Axiome de la paire : Si x et y sont deux ensembles, alors il existe un ensemble contenant x et y et eux seuls comme éléments. Cet ensemble se note {x,y}. À noter que x et y ne sont pas nécessairement distincts. Cet axiome est conséquence du schéma de remplacement mais pas du schéma de compréhension, aussi on peut l'omettre dans la théorie ZF mais il est indispensable dans la théorie Z.
4. Axiome de la réunion : Pour tout ensemble X, il existe un ensemble R dont les éléments sont précisément ceux des éléments de X et eux seuls.
5. Axiome de l'ensemble des parties : Pour tout ensemble E, il existe un ensemble dont les éléments sont précisément les sous-ensembles de E. Cet ensemble se note habituellement P(E).
6. Axiome de l'infini : Il existe un ensemble W dont est élément et tel que pour tout x appartenant à W, appartient aussi à W. On peut ensuite définir par compréhension l'intersection de tous les ensembles contenant et clos par cette opération : il s'agit de l'ensemble des nombres entiers tels que définis par von Neumann.
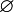
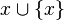
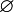
7. Schéma d'axiomes de compréhension ou de séparation : pour tout ensemble A et toute propriété P exprimée dans le langage, il existe un ensemble dont les éléments sont les éléments de A vérifiant P. Le schéma de compréhension est conséquence du schéma de remplacement qui suit.
8. Schéma d'axiomes de remplacement : Pour tout ensemble A et toute relation fonctionnelle P, formellement définie comme une proposition P(x,y) et telle que P(x,y) et P(x,z) impliquent que y = z, il existe un ensemble contenant précisément les images par P des éléments de l'ensemble d'origine A.
9. Axiome de fondation : Tout ensemble X non vide contient un élément y tel que X et y sont des ensembles disjoints (qui n'ont aucun élément en commun), ce qui se note . Cet axiome n'est pas toujours ajouté à Z ou ZF. On peut construire assez facilement comme sous-classe d'un modèle quelconque de ZF, un modèle de ZF vérifiant l'axiome de fondation. Les ensembles utiles au développement des mathématiques usuelles appartiennent à cette sous-classe, et donc cela a peu d'importance d'ajouter celui-ci ou non à la théorie pour ces développements. L'axiome de fondation n'est par exemple pas mentionné dans le livre de Halmos, dont le but est de présenter les aspects de la théorie des ensembles utiles pour le mathématicien non spécialiste de ce domaine. L'axiome de fondation est par contre très utile dans le domaine spécialisé de la théorie des ensembles, il permet de hiérarchiser l'univers ensembliste, de définir un rang ordinal (voir l'article axiome de fondation) ... Des théories des ensembles, extensions de ZF sans fondation, ont par ailleurs été développées, qui introduisent un axiome d'anti-fondation (il en existe plusieurs variantes) qui contredit directement l'axiome de fondation. L'anti-fondation est une idée assez ancienne (Dimitri Mirimanoff 1917, Paul Finsler 1926), mais ces théories ont connu un regain d'intérêt pour leur lien avec l'informatique théorique.
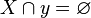
10. Axiome du choix : (version de Zermelo) Étant donné un ensemble X d'ensembles non vides mutuellement disjoints, il existe un ensemble y (l'ensemble de choix pour X) contenant exactement un élément pour chaque membre de X.
    L'axiome du choix reste controversé pour une minorité de mathématiciens. Des formes faibles existent, comme l'axiome du choix dépendant, très utile pour le développement de l'analyse réelle.