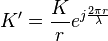Théorie de la diffraction - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Diffraction de Fresnel
Dans les conditions usuelles d'observation, les tailles de l'ouverture et du phénomène de diffraction observé sont petites devant la distance r d'observation. On a :
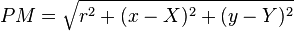
On peut donc utiliser un développement limité pour écrire:
![PM\simeq r\left[1+\frac{1}{2}\left(\frac{x-X}{r}\right)^2+ \frac{1}{2}\left(\frac{y-Y}{r}\right)^2\right]](https://static.techno-science.net/illustration/Definitions/autres/b/bb0e5f79e3466681f0769a3e30db2ce2_9e3c311d4e6429dde754a735cba750dc.png)
En remplaçant PM par cette expression dans l'exponentielle complexe et 1/PM par 1/r (cette approximation est ici suffisante car 1/PM n'est pas une fonction périodique), on obtient alors :
![E(M)=K'\iint_{\Sigma}E(P)\exp\left[ \frac{j\pi}{\lambda r}\left[(x-X)^2+(y-Y)^2\right]\right]dXdY](https://static.techno-science.net/illustration/Definitions/autres/e/ef3461365acf2cc45b78722a03c0fa08_3dbca228d9d378aa3393a57412ef0a25.png)
où