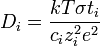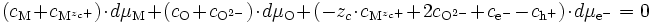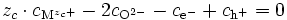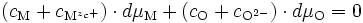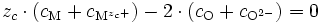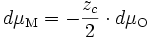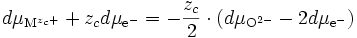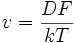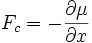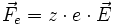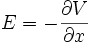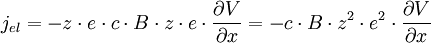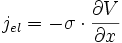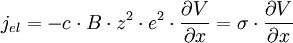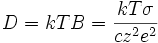Théorie de la cinétique d'oxydation de Wagner - Définition

Prérequis

Les prérequis pour cette étude sont :

• la loi de Fick, loi phénoménologique de la diffusion ;
• la loi de Nernst-Einstein, résultant de l'étude statistique du mouvement d'une particule sous l'effet combiné d'une force et de chocs aléatoires ;
• la loi d'Ohm sous sa forme microscopique ;
• la conduction électrique dans les oxydes cristallins
• la relation thermodynamique de Gibbs-Duhem

Équilibre thermodynamique

Dans cette partie, nous considèrerons pour simplifier que la migration, pour le métal ou bien l'oxygène, se fait par une seule espèce (ion interstitiel ou bien lacune, cf. Défaut cristallin et Notation de Kröger et Vink), et nous noterons :

• M pour désigner l'ion métallique en position normale dans l'oxyde M_M ;
• M^zc+ pour désigner l'ion mobile dans l'oxyde, c'est-à-dire soit l'ion interstitiel M_i^zc•, soit la lacune métallique V_M^zc ' ;
• O pour désigner l'ion oxygène en position normale O_O ;
• O^2- pour désigner l'ion mobile dans l'oxyde, O_i² ' ou V_O^2• ;
• e^- pour désigner les électrons libres e' et h⁺ les trous d'électrons h^•.

Notez que lorsqu'une lacune se déplace, cela équivaut globalement au déplacement en sens inverse d'un ion de charge opposée à la charge effective de la lacune.

Si l'on écrit la relation de Gibbs-Duhem, on obtient :

(E10)

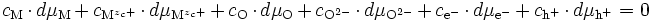
Écrivons maintenant les équilibres chimiques locaux :

• cations : M ⇌ M^zc+ + z_c e^- ⇒ dμ_M = dμ_Mzc+ + z_c dμ_e- (E11) ;
• anions : O + 2e^- ⇌ O^2- ⇒ dμ_O + 2 dμ_e- = dμ_O2- (E12);
• électrons et trous d'électron : Ø ⇌ e^- + h⁺ ⇒ 0 = dμ_e- + dμ_h+ soit dμ_e- = - dμ_h+ (E13).

La relation de Gibbs-Duhem () s'écrit donc :

L'électroneutralité s'écrit :

donc

Puisque nous sommes proches de la stœchiométrie, on peut écrire la neutralité électrique du cristal : l'ensemble des cations (en position interstitielle ou en position normale) contrebalance l'ensemble des anions (en position interstitielle ou en position normale) en ce qui concerne les charges :

La relation de Gibbs-Duhem devient donc au final

ou bien encore

et donc

(E14)

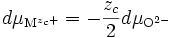
Migration sous l'effet d'un champ

Les espèces effectuant des sauts aléatoires, nous considérons le parcours moyen <X> d'une particule (atome, ion, électron libre, trou d'électron) pendant une durée τ. On peut définir la vitesse moyenne v comme étant

Si la particule est soumise à une force F, alors on peut relier la vitesse moyenne à la force et au coefficient de diffusion D par la loi de Nernst-Einstein :

k étant la constante de Boltzmann et T la température absolue. Si l'on prend la comparaison avec le frottement fluide (freinage du parachute), on peut écrire que la vitesse est proportionnelle à la force :

v = B⋅F

B étant la mobilité (Beweglichkeit) de l'espèce. On a donc la relation d'Einstein :

D = B⋅k⋅T (E4)

Le flux j, lui, résulte du mouvement sous l'effet de la force, qui tend à faire migrer les espèces et donc à créer un gradient de concentration, et de l'agitation thermique qui tend elle au contraire à uniformiser la concentration (loi de Fick). Comme on se place dans le cas d'un oxyde dont la composition est proche de la stœchiométrie, on suppose également que la variation de concentration est faible. Le flux peut donc s'écrire, par approximation :

j = v⋅c = c⋅B⋅F (E5)

c étant la concentration.

Potentiel chimique

La force F_c résultant du potentiel chimique μ peut s'écrire, à une dimension :

et donc () devient :

(E6)

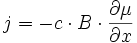
Champ électrique

Si une particule porte z charges élémentaires e, alors elle subit la force F_e (force électrostatique ou force de Coulomb) :

Le champ électrique E dérive d'un potentiel V, ce qui s'écrit à une dimension :

d'où, d'après (), un flux :

(E7)

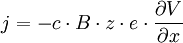
soit une densité de courant électrique (flux de charges) j_el valant d'après ()

On peut faire un parallèle avec le loi d'Ohm reliant cette densité de courant électrique j_el au gradient de potentiel :

σ étant la conductivité électrique. On a donc :

soit

σ = c⋅B⋅z²⋅e² (E8)

et donc d'après la relation d'Einstein () :

Lorsqu'il y a plusieurs porteurs de charge i, la conductivité totale σ est la somme des conductivités pour chaque espèce σ_i :

σ = ∑_i σ_i

On peut aussi écrire que chaque σ_i est une portion t_i de σ :

σ_i = t_i⋅σ

avec évidemment

∑_i = t_i = 1

Le coefficient t_i est appelé le « nombre de transport » de l'espèce i.

On obtient donc pour une espèce donnée :

(E9)