Théorie de Galois - Définition

Exemples

Petit théorème de Fermat

Le petit théorème de Fermat nous indique que si a est un entier et p un nombre premier alors:

Il est possible de démontrer ce théorème en remarquant que F_p le quotient de l'ensemble des nombres entiers par son idéal engendré par p est un corps, car p est un nombre premier. (F_p^*, .) est un groupe fini de cardinal p -1. Le théorème de Lagrange assure que tout élément de ce groupe à la puissance p -1 est égal à l'unité, ce qui démontre le théorème.

Conclusion : Ce cas est particulièrement aisé car la structure du corps est simple. Il illustre néanmoins le fait qu'une structure de corps est un outil utile en théorie algébrique des nombres. D'autres théorèmes d'arithmétique modulaire comme la loi de réciprocité quadratique demandent une compréhension beaucoup plus profonde de la structure des corps. C'est la raison pour laquelle la démonstration ne put être trouvée malgré leurs efforts par Euler ou Lagrange et qu'il fallut attendre Gauss et ses polynômes cyclotomiques pour conclure.

Duplication du cube

Une construction à la règle et au compas, celle de la duplication du cube est impossible

Soit L l'ensemble des éléments de la forme a + b.√2 où a et b sont des rationnels.

Montrons que L est un corps : L est clairement stable pour l'addition et le passage à l'opposé, et est donc un groupe additif. Il est stable pour la multiplication et le passage à l'inverse des éléments non nuls, en effet:

Ces deux dernières propositions montrent que L est un sous-corps des nombres réels. L est aussi un espace vectoriel de dimension deux sur les nombres rationnels, car il possède pour base 1 et √2. Un tel corps s'appelle une extension quadratique.

Montrons que L ne contient pas la racine cubique de deux : Soit l un élément de L, alors de l ² est une combinaison linéaire à coefficients rationnels de 1 et √2 car ces deux éléments forment une base et l ² est un élément de L. il existe donc deux rationnels α et β tel que l'égalité suivante est vraie:

Et pour tout élément l de L il existe un polynôme de degré inférieur ou égal à deux ayant pour racine l. Or, le plus petit degré du polynôme non nul à coefficients rationnels qui annule la racine cubique de deux est trois, et la proposition est démontrée.

Conclusion : Wantzel a démontré que les nombres constructibles à la règle et au compas sont soit dans une extension quadratique, soit dans une extension quadratique dont les coefficients sont pris dans une extension quadratique et ainsi de suite. On parle alors de tour d'extension quadratique. Il est possible de démontrer par un raisonnement analogue à celui présenté ici que la racine cubique de deux n'est pas élément d'une tour d'extension quadratique. Voilà pourquoi la duplication du cube est impossible. Le choix judicieux de corps particuliers est la clé de la résolution de cette antique conjecture.

Équation cubique

Ars Magna de Girolamo Cardano 1545

Considérons un exemple d'équation du troisième degré :

Détermination d'un élément du groupe de Galois : Le polynôme P[X] est un polynôme irréductible à coefficients rationnels. La théorie de Galois nous indique qu'il existe un corps L qui est une extension des rationnels contenant toutes les racines de P[X]. Cette extension est de dimension six. De plus, il existe un sous-corps K de L tel que L est de dimension trois sur K et j la première racine cubique de l'unité est élément de K. Le groupe de Galois de L sur K est l'ensemble des automorphismes de corps de L laissant invariant tout élément de K. La théorie de Galois nous indique que ce groupe a trois éléments, soit g un élément du groupe différent de l'identité.

Diagonalisation de g : Le théorème de Lagrange nous assure que g³ est égal à l'identité. Si l est un élément non nul de L, alors l, g(l) et g²(l) forment une base de L sur K. Considérant g comme opérateur linéaire, son polynôme caractéristique est X³ - 1 et ses valeurs propres sont 1, j et j². Il existe une base (u, v, w) de L sur K constituée de vecteurs propres, car le nombre de valeurs propres est égal à la dimension de L sur K. On a donc g(u)=j·u, g(v)=j²·v et g(w)=w. De plus, 1 + j + j² = 0.

Détermination de l'image des racines par g : Soit x₁, une racine de P[X]. L'image d'une racine par g est une racine, en effet:

On en déduit que x₁, g(x₁) et g²(x₁) sont les trois racines de P. On peut repésenter x₁ comme somme de vecteurs propres de g: x₁ = u + v + w (léger abus de notation: w sera en l'occurrence 0, ne formant plus une base comme ci-dessus). Les trois égalités suivantes sont alors vérifiées:

Calcul des valeurs des racines : Il suffit d'utiliser les relations entre coefficients et racines pour montrer que :

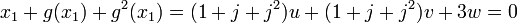, donc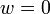

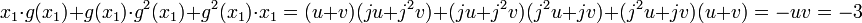, donc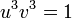

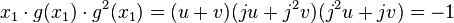, donc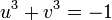

On en déduit que u ³ et v ³ vérifient l'équation X² + X + 1 = 0. Ce qui permet de conclure que x₁ est égal à 2 cos(2π/9), 2 cos(8π/9) ou 2 cos(14π/9).

Conclusion : Le groupe de Galois, permet la résolution de l'équation cubique par une diagonalisation d'un endomorphisme. La méthode est généralisable si et seulement si le groupe de Galois possède de bonnes propriétés, en fait s'il est résoluble.

Synthèse

Ces exemples ont un point commun, ce sont les propriétés des structures algébriques qui permettent de trouver les solutions. Pour le premier exemple, la propriété démontrée par Lagrange sur les groupes (et donc les groupes multiplicatifs des corps) finis permet de conclure. Dans le deuxième exemple, ce sont les propriétés associées sur la dimension d'un l'espace vectoriel qui sont utilisées. Dans le troisième cas, sont utilisés les propriétés des corps et de leurs extensions, des groupes avec le théorème de Lagrange et celle des espaces vectoriels avec les propriétés de réduction d'endomorphisme dans le cas où le polynôme minimal est scindé.

La théorie de Galois offre une richesse dans les structures algébriques permettant de résoudre nombre de cas très différents et dans des domaines éloignés.